三角関数の合成（調和加法定理）

TL;DR

三角関数の合成（調和加法定理）

• \[a\sin \theta + b\cos \theta = \sqrt{a^{2}+b^{2}} \sin(\theta+\alpha)\]

\[(ただし、\ \cos \alpha = \frac{a}{\sqrt{a^{2}+b^{2}}},\ \sin \alpha = \frac{b}{\sqrt{a^{2}+b^{2}}})\]

• \[a\sin \theta + b\cos \theta = \sqrt{a^{2}+b^{2}} \cos(\theta-\beta)\]

\[(ただし、\ \cos \beta = \frac{b}{\sqrt{a^{2}+b^{2}}},\ \sin \beta = \frac{a}{\sqrt{a^{2}+b^{2}}})\]

前提知識

• 三角関数の加法定理

三角関数の合成（調和加法定理）

$f(\theta) = a \cos \theta + b \sin \theta$のような三角関数の和の形で構成される関数$f(\theta)$に対して、$f(\theta)=\sqrt{a^2+b^2} \sin(\theta+\alpha) = \sqrt{a^2+b^2} \cos(\theta-\beta)$を満たす実数$\alpha$、$\beta$が常に存在します。

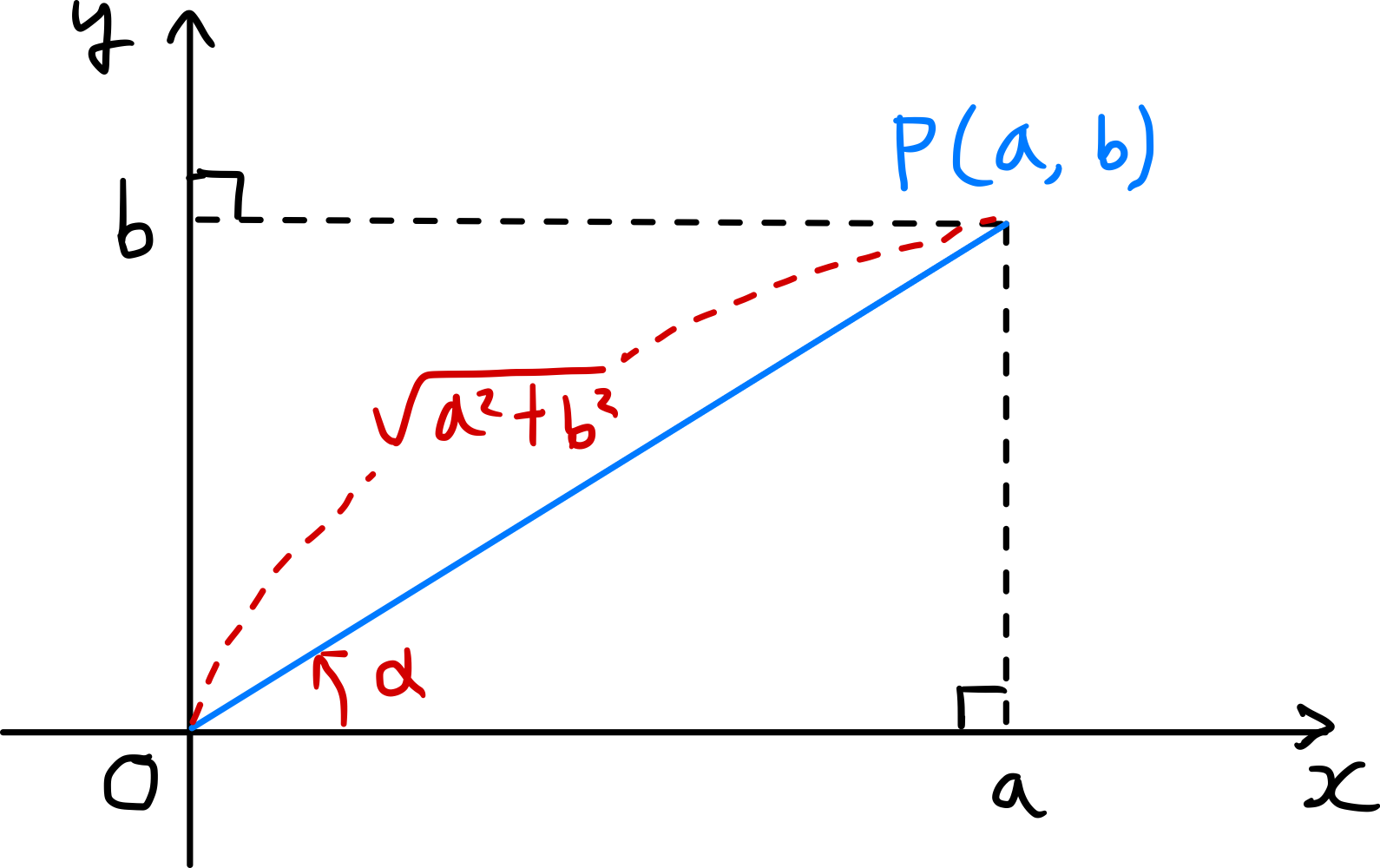
図のように座標平面上に点$P(a,b)$をとり、線分$\overline{OP}$と$x$軸の正の方向がなす角の大きさを$\alpha$とすると

\[\overline{OP} = \sqrt{a^2+b^2}\]

であり

\[\cos \alpha = \frac{a}{\sqrt{a^{2} + b^{2}}},\ \sin \alpha = \frac{b}{\sqrt{a^{2} + b^{2}}} \tag{1}\]

となります。このとき、

\[\begin{align*} a \sin \theta + b \cos \theta &= \sqrt{a^{2}+b^{2}} \left(\frac{a}{\sqrt{a^{2}+b^{2}}}\sin \theta + \frac{b}{\sqrt{a^{2}+b^{2}}}\cos \theta \right) \\ &= \sqrt{a^{2}+b^{2}}(\cos \alpha \sin \theta + \sin \alpha \cos \theta) \\ &= \sqrt{a^{2}+b^{2}} \sin(\theta + \alpha). \tag{2} \end{align*}\]

同様の方法で点$P^{\prime}(b,a)$をとり、線分$\overline{OP^{\prime}}$と$x$軸の正の方向がなす角の大きさを$\beta$とすると、次を得ます。

\[a \sin \theta + b \cos \theta = \sqrt{a^{2}+b^{2}}\cos(\theta-\beta). \tag{3}\] \[ただし、\ \cos \beta = \frac{b}{\sqrt{a^{2}+b^{2}}},\ \sin \beta = \frac{a}{\sqrt{a^{2}+b^{2}}}.\]

このように$a \sin \theta + b \sin \theta$の形の三角関数を$r\sin(\theta+\alpha)$または$r\cos(\theta-\beta)$の形に変形することを三角関数の合成（調和加法）と呼びます。

例題

関数$f(\theta)=-\sqrt{3}\sin \theta + \cos \left(\theta - \frac{\pi}{3} \right)$とするとき、区間$[0, 2\pi]$における関数$f(\theta)$の最大値と最小値を求めなさい。

1. $a\sin\theta + b\cos\theta$の形に変形

三角関数の加法定理を用いて与えられた関数式を変形すると

\[\begin{align*} f(\theta) &= -\sqrt{3}\sin \theta + \cos \left(\theta - \frac{\pi}{3} \right) \\ &= -\sqrt{3}\sin \theta + \left( \cos\theta \cos\frac{\pi}{3} + \sin\theta \sin\frac{\pi}{3} \right) \\ &= -\frac{\sqrt{3}}{2}\sin\theta + \frac{1}{2}\cos\theta . \end{align*}\]

2. $r\sin(\theta+\alpha)$の形に変形

$a=-\frac{\sqrt{3}}{2}$、$b=\frac{1}{2}$とおくと、

\[r = \sqrt{a^2+b^2} = \sqrt{\frac{3}{4}+\frac{1}{4}} = 1\]

となります。

また、$0 \leq \alpha<2\pi$で$\cos\alpha = a$、$\sin\alpha = b$となる実数$\alpha$の値は1つ存在します。特殊角に対する三角比の値から、$\alpha = \frac{5}{6}\pi$であることがわかります。

したがって、与えられた関数$f(\theta)$を$r\sin(\theta+\alpha)$の形に変形すると次のようになります。

\[f(\theta) = \sin \left(\theta + \frac{5\pi}{6} \right).\]

3. 与えられた区間での最大値と最小値を求める

関数$f(\theta) = \sin \left(\theta + \frac{5\pi}{6} \right)$は$2\pi$を周期とする周期関数であり、与えられた区間で最大値$1$、最小値$-1$をとります。

\[\therefore M=1,\ m=-1\]