三角関数の加法定理

三角関数の定義

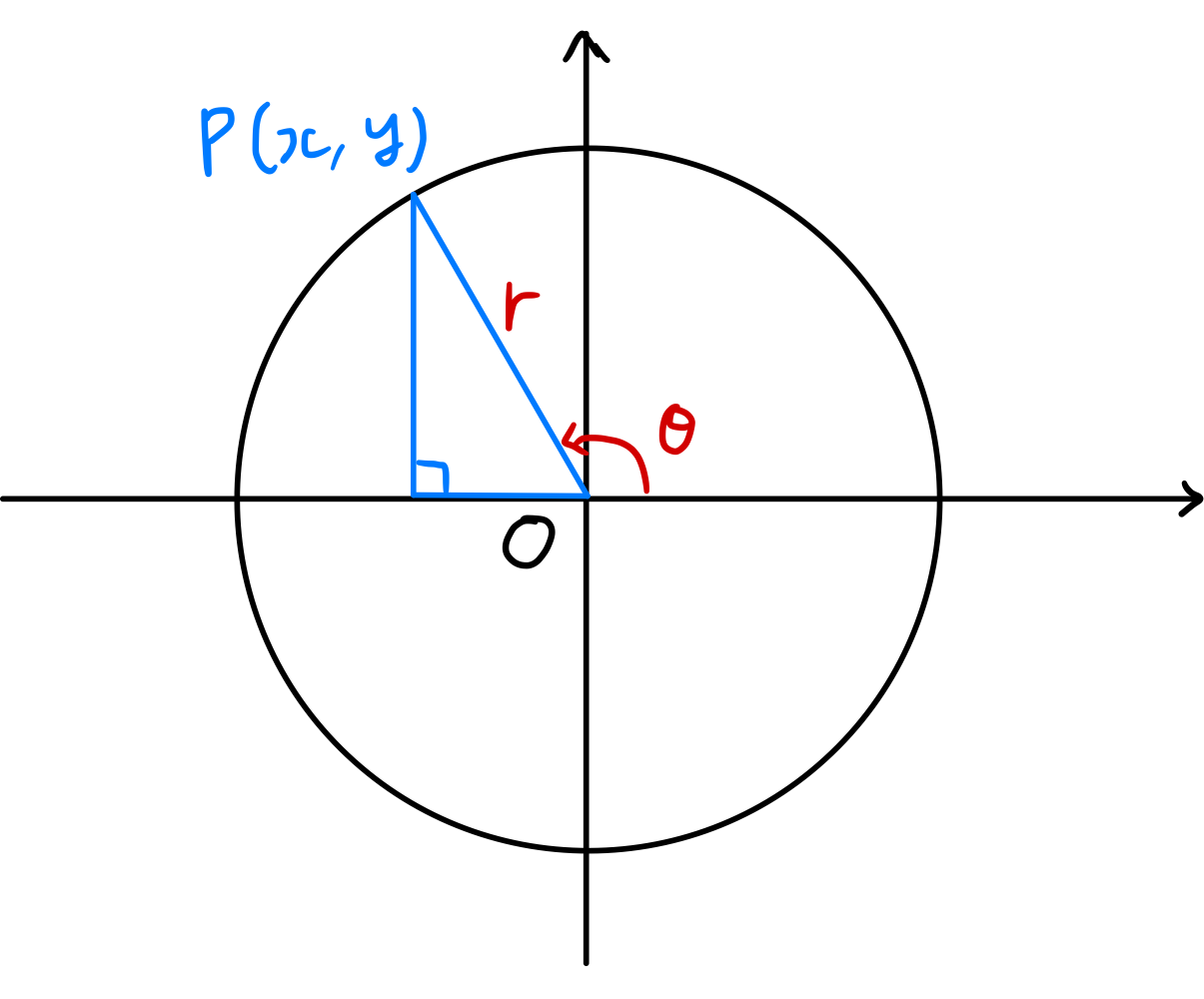図のように、動径 $\overline{OP}$ が $x$ 軸の正の方向となす角の大きさを $\theta$ とするとき、 \(\begin{gather}\begin{split} \sin \theta = \frac { y } { r } ,\; \cos \theta = \frac { x } { r } ,\; \tan \theta = \frac { y } { x } \\ \csc \theta = \frac { r } { y } ,\; \sec \theta = \frac { r } { x } ,\; \cot \theta = \frac { x } { y } \end{split}\end{gather}\) と定義し、これらを総称して三角関数と呼ぶ。

三角関数間の関係

1. \[\csc \theta = \frac { 1 } { \sin \theta } ,\; \sec \theta = \frac { 1 } { \cos \theta } ,\; \cot \theta = \frac { 1 } { \tan \theta } \tag{2}\]
2. \[\tan \theta = \frac { \sin \theta } { \cos \theta } ,\; \cot \theta = \frac { \cos \theta } { \sin \theta } \tag{3}\]
3. \[\tag{4} \begin{gather*} \sin ^ { 2 } \theta + \cos ^ { 2 } \theta = 1 \\ \tan ^ { 2 } \theta + 1 = \sec ^ { 2 } \theta \\ 1 + \cot ^ { 2 } \theta = \csc ^ { 2 } \theta \end{gather*}\]

三角関数の加法定理

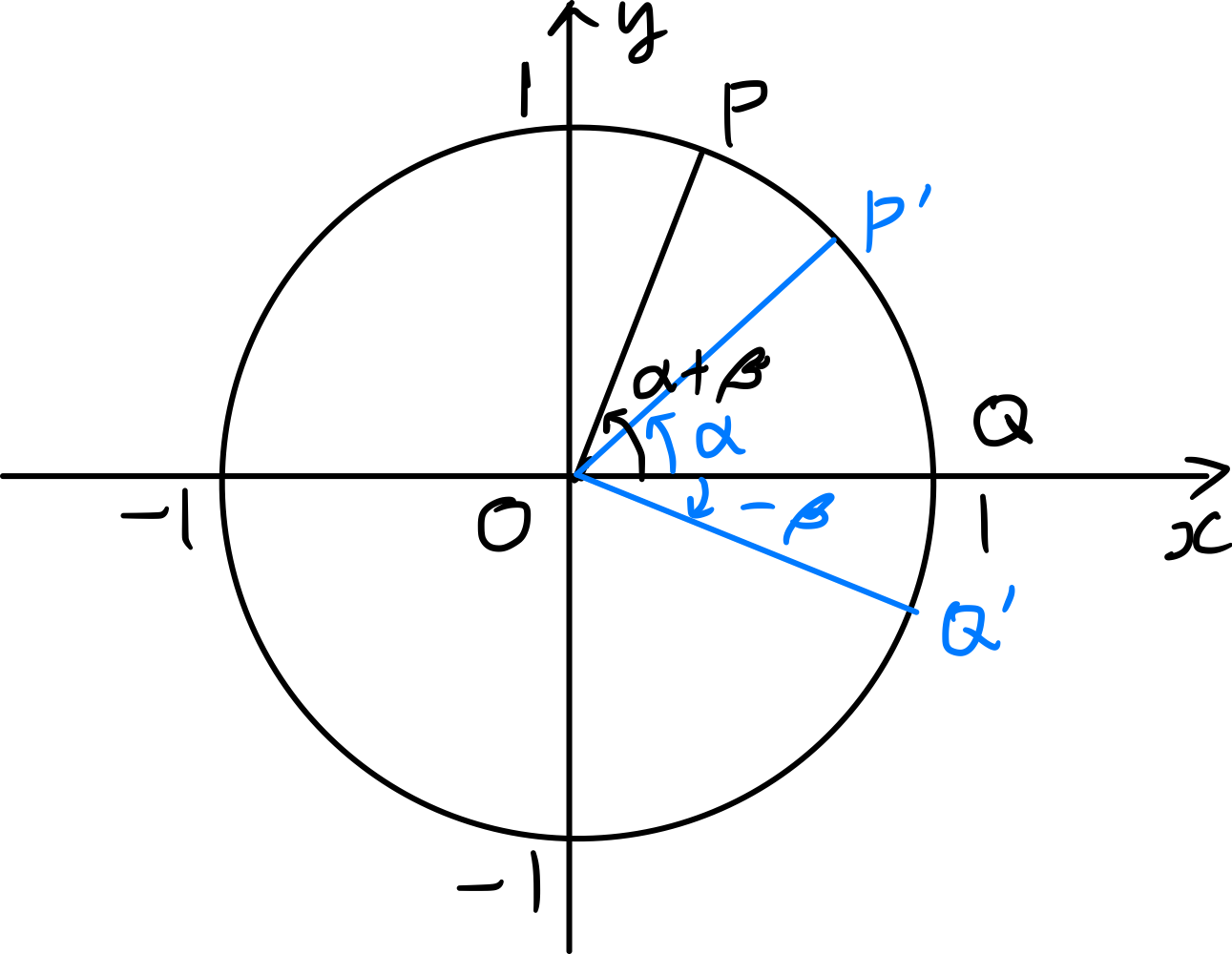図のように、$x$ 軸の正の方向となす角の大きさが $\alpha+\beta,\, 0,\, \alpha,\, -\beta$ である4つの動径が単位円と交わる点をそれぞれ $P, Q, P^{\prime}, Q^{\prime}$ とする。

2点 $P, Q$ の座標は

\[P(\cos(\alpha+\beta), \sin(\alpha+\beta)),\; Q(1,0)\]

であるため

\[\begin{align*} \overline { P^ { \prime } Q^ { \prime } } ^2&= \{ \cos \alpha - \cos ( - \beta ) \} ^ { 2 } + \{ \sin \alpha - \sin ( - \beta ) \} ^ { 2 } \\ &= 2 - 2 \cos \alpha \cos ( - \beta ) - 2 \sin \alpha \sin ( - \beta ) \\ &= 2 - 2 \cos \alpha \cos \beta + 2 \sin \alpha \sin \beta. \end{align*}\]

$\overline{PQ}=\overline{P^{\prime} Q^{\prime}}$ であるため $2 - 2 \cos ( \alpha + \beta ) = 2 - 2 \cos \alpha \cos \beta + 2 \sin \alpha \sin \beta.$

\[\therefore \cos ( \alpha + \beta ) = \cos \alpha \cos \beta - \sin \alpha \sin \beta. \label{eqn:cos_1} \tag{5}\]

上式の $\beta$ に $-\beta$ を代入して整理すると

\[\cos ( \alpha - \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \label{eqn:cos_2} \tag{6}\]

$\cos ( \frac { \pi } { 2 } - \theta ) = \sin \theta ,\, \sin ( \frac { \pi } { 2 } - \theta ) = \cos \theta$ であるため

\[\begin{align*} \sin ( \alpha + \beta ) &= \cos ( \frac { \pi } { 2 } - ( \alpha + \beta ) ) = \cos ( ( \frac { \pi } { 2 } - \alpha ) - \beta) \\ &= \cos ( \frac { \pi } { 2 } - x ) \cos \beta + \sin ( \frac { \pi } { 2 } - \alpha ) \sin \beta \\ &= \sin \alpha \cos \beta + \cos \alpha \sin \beta. \end{align*}\] \[\therefore \sin ( \alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta. \label{eqn:sin_1} \tag{7}\]

この式の $\beta$ に $-\beta$ を代入して整理すると

\[\sin ( \alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta. \label{eqn:sin_2} \tag{8}\]

最後に、

\[\tan ( \alpha + \beta ) = \frac { \sin ( \alpha + \beta ) } { \cos ( \alpha + \beta ) } = \frac { \sin \alpha \cos \beta + \cos \alpha \sin \beta } { \cos \alpha \cos \beta - \sin \alpha \sin \beta }\]

において分母と分子をそれぞれ $\cos{\alpha} \cos{\beta}$ で割って整理すると

\[\tan ( \alpha + \beta ) = \frac { \tan \alpha + \tan \beta } { 1 - \tan \alpha \tan \beta } \label{eqn:tan_1} \tag{9}\]

となり、この式の $\beta$ に $-\beta$ を代入して整理すると

\[\tan ( \alpha - \beta ) = \frac { \tan \alpha - \tan \beta } { 1 + \tan \alpha \tan \beta } \label{eqn:tan_2} \tag{10}\]

となる。

傾きが与えられた2直線がなす鋭角の大きさ

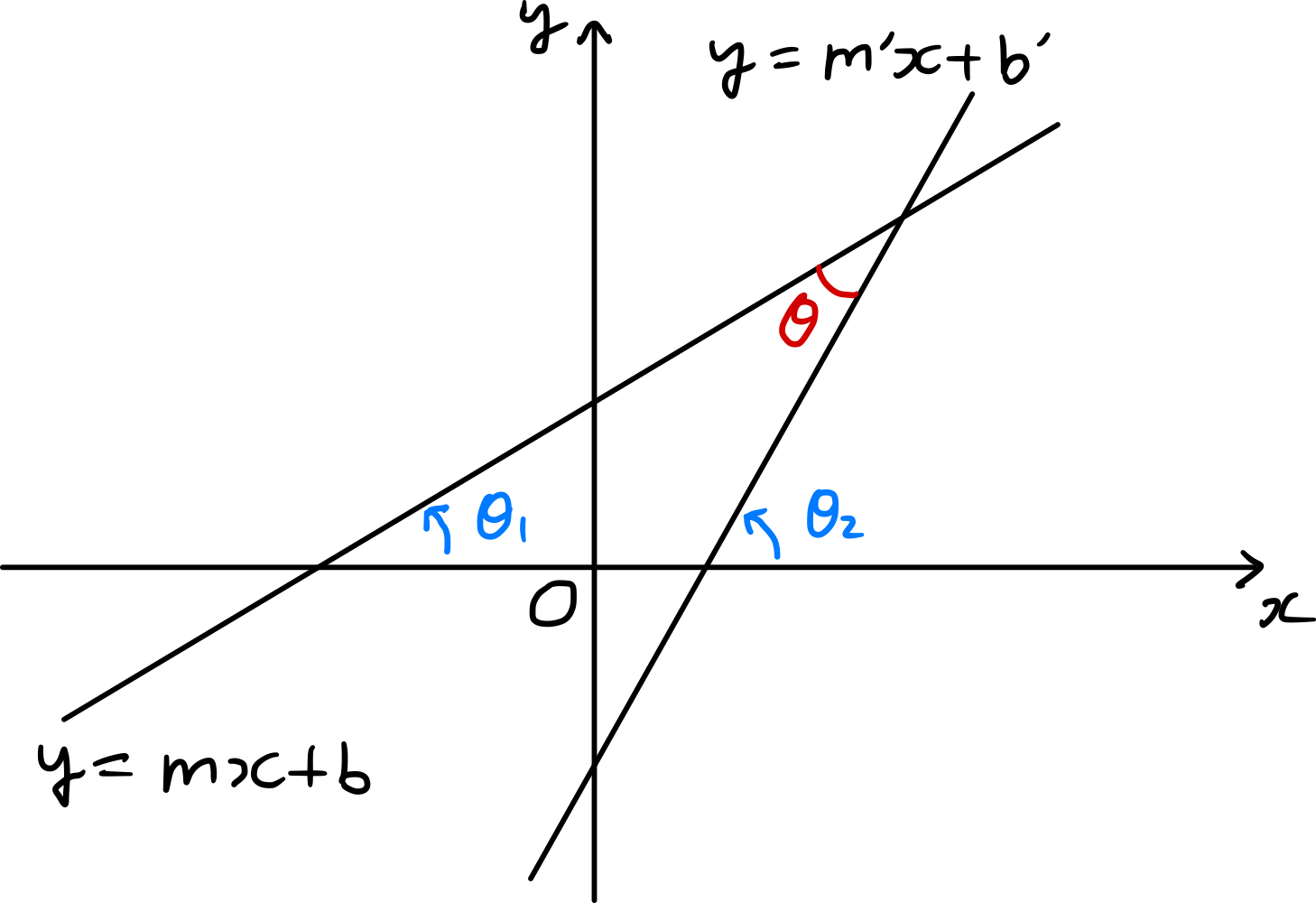式 ($\ref{eqn:tan_2}$) を用いると、傾きが与えられた2直線がなす鋭角の大きさを求めることができる。2直線 $y=mx+b$, $y=m^{\prime} x+b^{\prime}$ が $x$ 軸の正の方向となす角の大きさをそれぞれ $\theta_{1}$, $\theta_{2}$ とすると

\[\tan{\theta_{1}}=m,\, \tan{\theta_{2}}=m^{\prime}\]

であるため、2直線がなす鋭角の大きさを $\theta$ とすると

\[\tag{11} \begin{align*} \tan{\theta}&=\left\vert \tan{\theta_{2}-\theta_{1}} \right\vert=\left\vert \frac{\tan{\theta_2}-\tan{\theta_1}}{1+\tan{\theta_1}\tan{\theta_2}}\right\vert \\ &=\left\vert \frac{m-m^{\prime}}{1+mm^{\prime}} \right\vert. \end{align*}\]