Théorème d'addition harmonique

TL;DR

Théorème d’addition harmonique

• \[a\sin \theta + b\cos \theta = \sqrt{a^{2}+b^{2}} \sin(\theta+\alpha)\]

\[(\text{où}\ \cos \alpha = \frac{a}{\sqrt{a^{2}+b^{2}}},\ \sin \alpha = \frac{b}{\sqrt{a^{2}+b^{2}}})\]

• \[a\sin \theta + b\cos \theta = \sqrt{a^{2}+b^{2}} \cos(\theta-\beta)\]

\[(\text{où}\ \cos \beta = \frac{b}{\sqrt{a^{2}+b^{2}}},\ \sin \beta = \frac{a}{\sqrt{a^{2}+b^{2}}})\]

Prérequis

• Formules d’addition trigonométriques

Théorème d’addition harmonique

Pour une fonction $f(\theta) = a \cos \theta + b \sin \theta$ composée d’une somme de fonctions trigonométriques, il existe toujours des nombres réels $\alpha$ et $\beta$ tels que $f(\theta)=\sqrt{a^2+b^2} \sin(\theta+\alpha) = \sqrt{a^2+b^2} \cos(\theta-\beta)$.

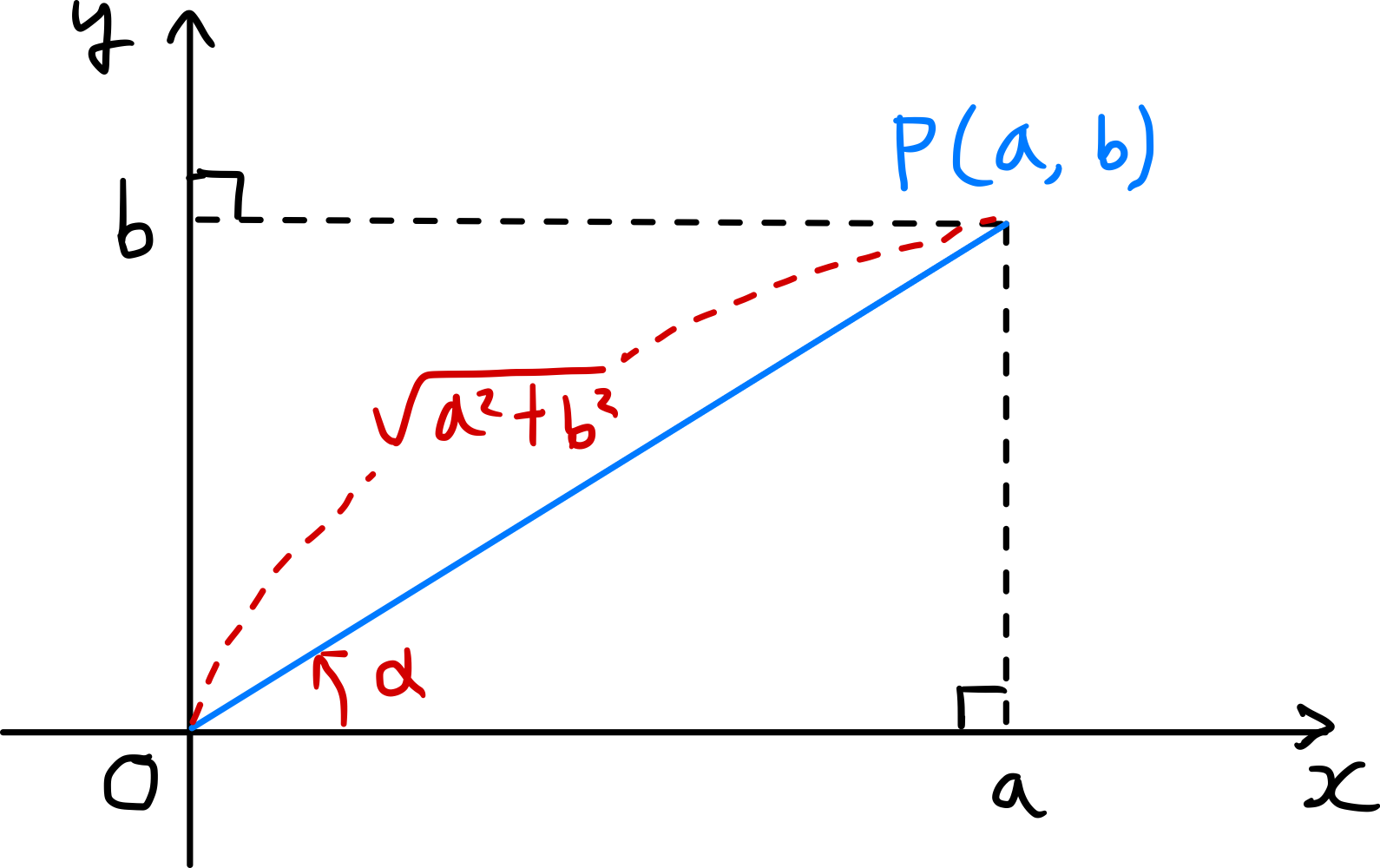
Comme illustré sur la figure, prenons un point $P(a,b)$ sur le plan de coordonnées et soit $\alpha$ l’angle formé entre le segment $\overline{OP}$ et la direction positive de l’axe $x$. Alors,

\[\overline{OP} = \sqrt{a^2+b^2}\]

et

\[\cos \alpha = \frac{a}{\sqrt{a^{2} + b^{2}}},\ \sin \alpha = \frac{b}{\sqrt{a^{2} + b^{2}}} \tag{1}\]

Dans ce cas,

\[\begin{align*} a \sin \theta + b \cos \theta &= \sqrt{a^{2}+b^{2}} \left(\frac{a}{\sqrt{a^{2}+b^{2}}}\sin \theta + \frac{b}{\sqrt{a^{2}+b^{2}}}\cos \theta \right) \\ &= \sqrt{a^{2}+b^{2}}(\cos \alpha \sin \theta + \sin \alpha \cos \theta) \\ &= \sqrt{a^{2}+b^{2}} \sin(\theta + \alpha). \tag{2} \end{align*}\]

De la même manière, en prenant un point $P^{\prime}(b,a)$ et en définissant $\beta$ comme l’angle formé entre le segment $\overline{OP^{\prime}}$ et la direction positive de l’axe $x$, nous obtenons :

\[a \sin \theta + b \cos \theta = \sqrt{a^{2}+b^{2}}\cos(\theta-\beta). \tag{3}\] \[\text{où}\ \cos \beta = \frac{b}{\sqrt{a^{2}+b^{2}}},\ \sin \beta = \frac{a}{\sqrt{a^{2}+b^{2}}}.\]

Cette transformation d’une fonction trigonométrique de la forme $a \sin \theta + b \sin \theta$ en une forme $r\sin(\theta+\alpha)$ ou $r\cos(\theta-\beta)$ est appelée addition harmonique.

Exemple

Soit la fonction $f(\theta)=-\sqrt{3}\sin \theta + \cos \left(\theta - \frac{\pi}{3} \right)$. Trouvez les valeurs maximale et minimale de la fonction $f(\theta)$ dans l’intervalle $[0, 2\pi]$.

1. Transformation en forme $a\sin\theta + b\cos\theta$

En utilisant les formules d’addition trigonométriques, nous transformons la fonction donnée :

\[\begin{align*} f(\theta) &= -\sqrt{3}\sin \theta + \cos \left(\theta - \frac{\pi}{3} \right) \\ &= -\sqrt{3}\sin \theta + \left( \cos\theta \cos\frac{\pi}{3} + \sin\theta \sin\frac{\pi}{3} \right) \\ &= -\frac{\sqrt{3}}{2}\sin\theta + \frac{1}{2}\cos\theta . \end{align*}\]

2. Transformation en forme $r\sin(\theta+\alpha)$

En posant $a=-\frac{\sqrt{3}}{2}$ et $b=\frac{1}{2}$, nous obtenons :

\[r = \sqrt{a^2+b^2} = \sqrt{\frac{3}{4}+\frac{1}{4}} = 1\]

De plus, il existe une valeur réelle unique $\alpha$ telle que $0 \leq \alpha<2\pi$, $\cos\alpha = a$, et $\sin\alpha = b$. À partir des valeurs trigonométriques des angles spéciaux, nous pouvons déduire que $\alpha = \frac{5}{6}\pi$.

Par conséquent, la fonction donnée $f(\theta)$ transformée en forme $r\sin(\theta+\alpha)$ devient :

\[f(\theta) = \sin \left(\theta + \frac{5\pi}{6} \right).\]

3. Trouver les valeurs maximale et minimale dans l’intervalle donné

La fonction $f(\theta) = \sin \left(\theta + \frac{5\pi}{6} \right)$ est une fonction périodique de période $2\pi$, et dans l’intervalle donné, elle atteint une valeur maximale de $1$ et une valeur minimale de $-1$.

\[\therefore M=1,\ m=-1\]