Formules d'addition des fonctions trigonométriques
Examinons les définitions des fonctions trigonométriques et les relations entre elles, puis dérivons les formules d'addition trigonométriques et les formules dérivées.
Définition des fonctions trigonométriques
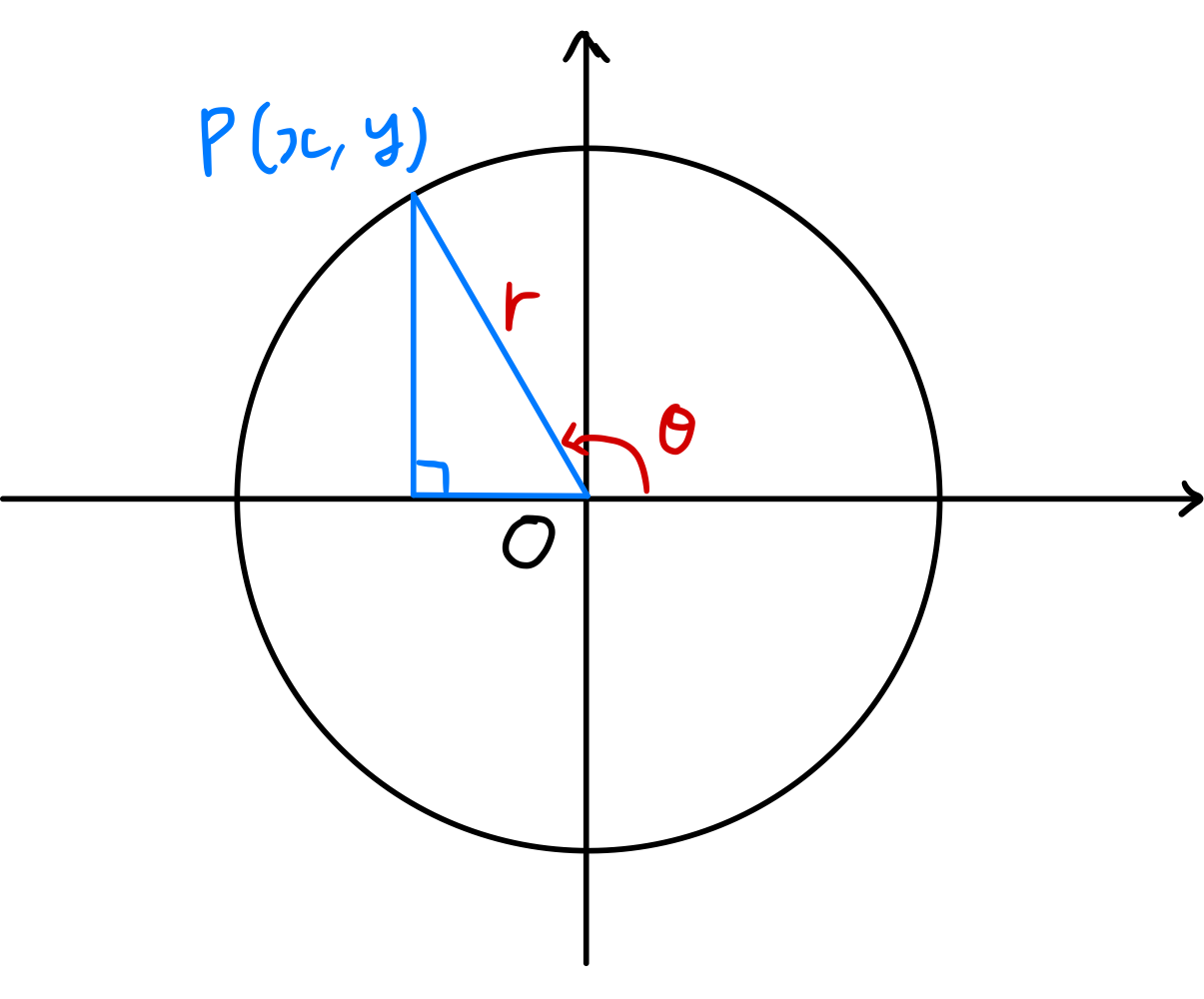Comme illustré sur la figure, lorsque la taille de l’angle formé par le rayon vecteur $\overline{OP}$ et la direction positive de l’axe $x$ est $\theta$, \(\begin{gather}\begin{split} \sin \theta = \frac { y } { r } ,\; \cos \theta = \frac { x } { r } ,\; \tan \theta = \frac { y } { x } \\ \csc \theta = \frac { r } { y } ,\; \sec \theta = \frac { r } { x } ,\; \cot \theta = \frac { x } { y } \end{split}\end{gather}\) sont définies ainsi, et collectivement appelées fonctions trigonométriques.
Relations entre les fonctions trigonométriques
- \[\csc \theta = \frac { 1 } { \sin \theta } ,\; \sec \theta = \frac { 1 } { \cos \theta } ,\; \cot \theta = \frac { 1 } { \tan \theta } \tag{2}\]
- \[\tan \theta = \frac { \sin \theta } { \cos \theta } ,\; \cot \theta = \frac { \cos \theta } { \sin \theta } \tag{3}\]
- \[\tag{4} \begin{gather*} \sin ^ { 2 } \theta + \cos ^ { 2 } \theta = 1 \\ \tan ^ { 2 } \theta + 1 = \sec ^ { 2 } \theta \\ 1 + \cot ^ { 2 } \theta = \csc ^ { 2 } \theta \end{gather*}\]
Formules d’addition trigonométriques
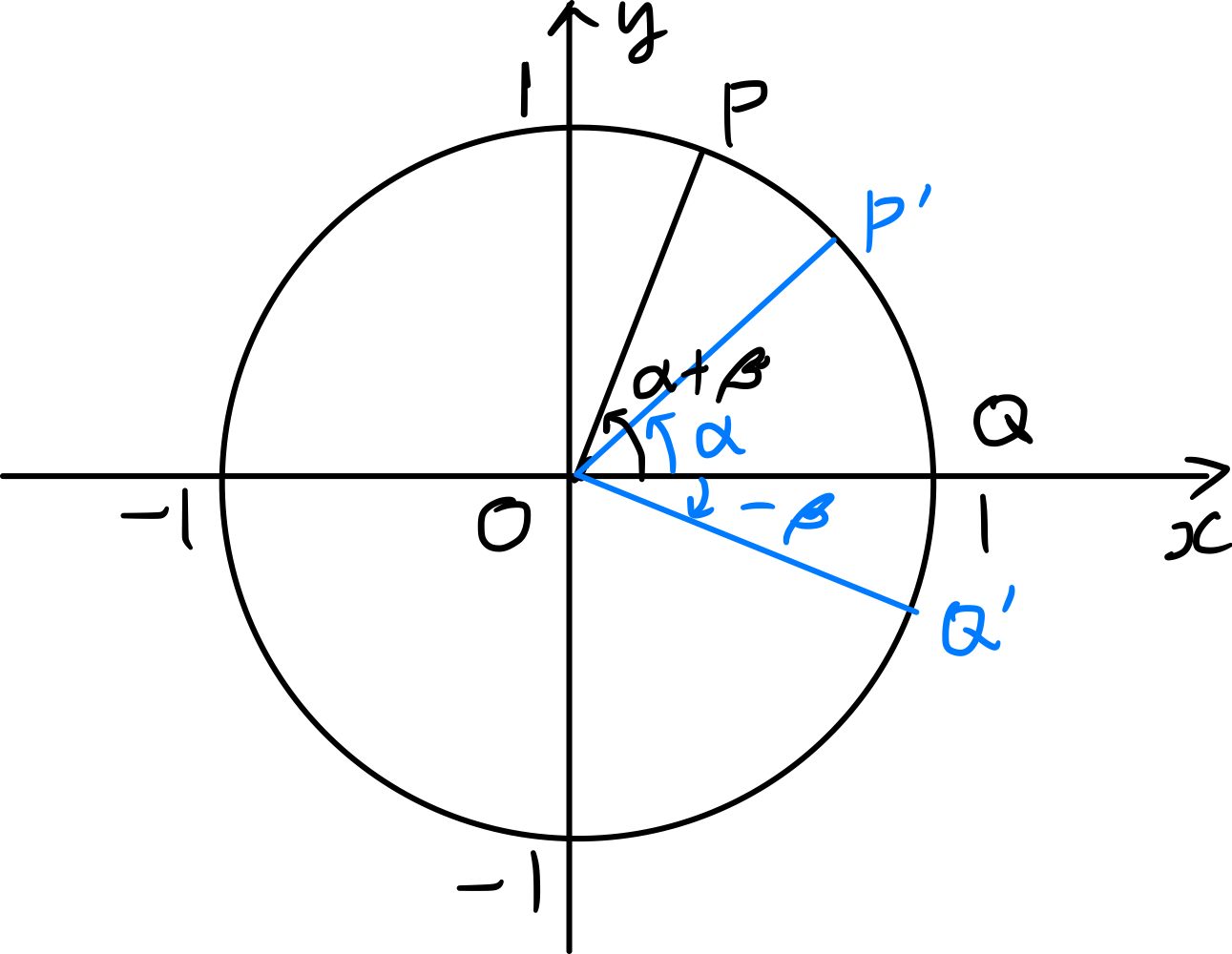Comme illustré sur la figure, soit $P, Q, P^{\prime}, Q^{\prime}$ les points où quatre rayons vecteurs formant des angles de $\alpha+\beta,\, 0,\, \alpha,\, -\beta$ avec la direction positive de l’axe $x$ rencontrent le cercle unitaire.
Les coordonnées des deux points $P, Q$ sont
\[P(\cos(\alpha+\beta), \sin(\alpha+\beta)),\; Q(1,0)\]donc
\[\begin{align*} \overline { P^ { \prime } Q^ { \prime } } ^2&= \{ \cos \alpha - \cos ( - \beta ) \} ^ { 2 } + \{ \sin \alpha - \sin ( - \beta ) \} ^ { 2 } \\ &= 2 - 2 \cos \alpha \cos ( - \beta ) - 2 \sin \alpha \sin ( - \beta ) \\ &= 2 - 2 \cos \alpha \cos \beta + 2 \sin \alpha \sin \beta. \end{align*}\]Comme $\overline{PQ}=\overline{P^{\prime} Q^{\prime}}$, on a $2 - 2 \cos ( \alpha + \beta ) = 2 - 2 \cos \alpha \cos \beta + 2 \sin \alpha \sin \beta.$
\[\therefore \cos ( \alpha + \beta ) = \cos \alpha \cos \beta - \sin \alpha \sin \beta. \label{eqn:cos_1} \tag{5}\]En substituant $-\beta$ à $\beta$ dans l’équation ci-dessus et en réarrangeant, on obtient
\[\cos ( \alpha - \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \label{eqn:cos_2} \tag{6}\]Comme $\cos ( \frac { \pi } { 2 } - \theta ) = \sin \theta ,\, \sin ( \frac { \pi } { 2 } - \theta ) = \cos \theta$,
\[\begin{align*} \sin ( \alpha + \beta ) &= \cos ( \frac { \pi } { 2 } - ( \alpha + \beta ) ) = \cos ( ( \frac { \pi } { 2 } - \alpha ) - \beta) \\ &= \cos ( \frac { \pi } { 2 } - x ) \cos \beta + \sin ( \frac { \pi } { 2 } - \alpha ) \sin \beta \\ &= \sin \alpha \cos \beta + \cos \alpha \sin \beta. \end{align*}\] \[\therefore \sin ( \alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta. \label{eqn:sin_1} \tag{7}\]En substituant $-\beta$ à $\beta$ dans cette équation et en réarrangeant, on obtient
\[\sin ( \alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta. \label{eqn:sin_2} \tag{8}\]Enfin,
\[\tan ( \alpha + \beta ) = \frac { \sin ( \alpha + \beta ) } { \cos ( \alpha + \beta ) } = \frac { \sin \alpha \cos \beta + \cos \alpha \sin \beta } { \cos \alpha \cos \beta - \sin \alpha \sin \beta }\]En divisant le numérateur et le dénominateur par $\cos{\alpha} \cos{\beta}$ et en réarrangeant, on obtient
\[\tan ( \alpha + \beta ) = \frac { \tan \alpha + \tan \beta } { 1 - \tan \alpha \tan \beta } \label{eqn:tan_1} \tag{9}\]et en substituant $-\beta$ à $\beta$ dans cette équation et en réarrangeant, on obtient
\[\tan ( \alpha - \beta ) = \frac { \tan \alpha - \tan \beta } { 1 + \tan \alpha \tan \beta } \label{eqn:tan_2} \tag{10}\]Angle aigu formé par deux droites de pentes données
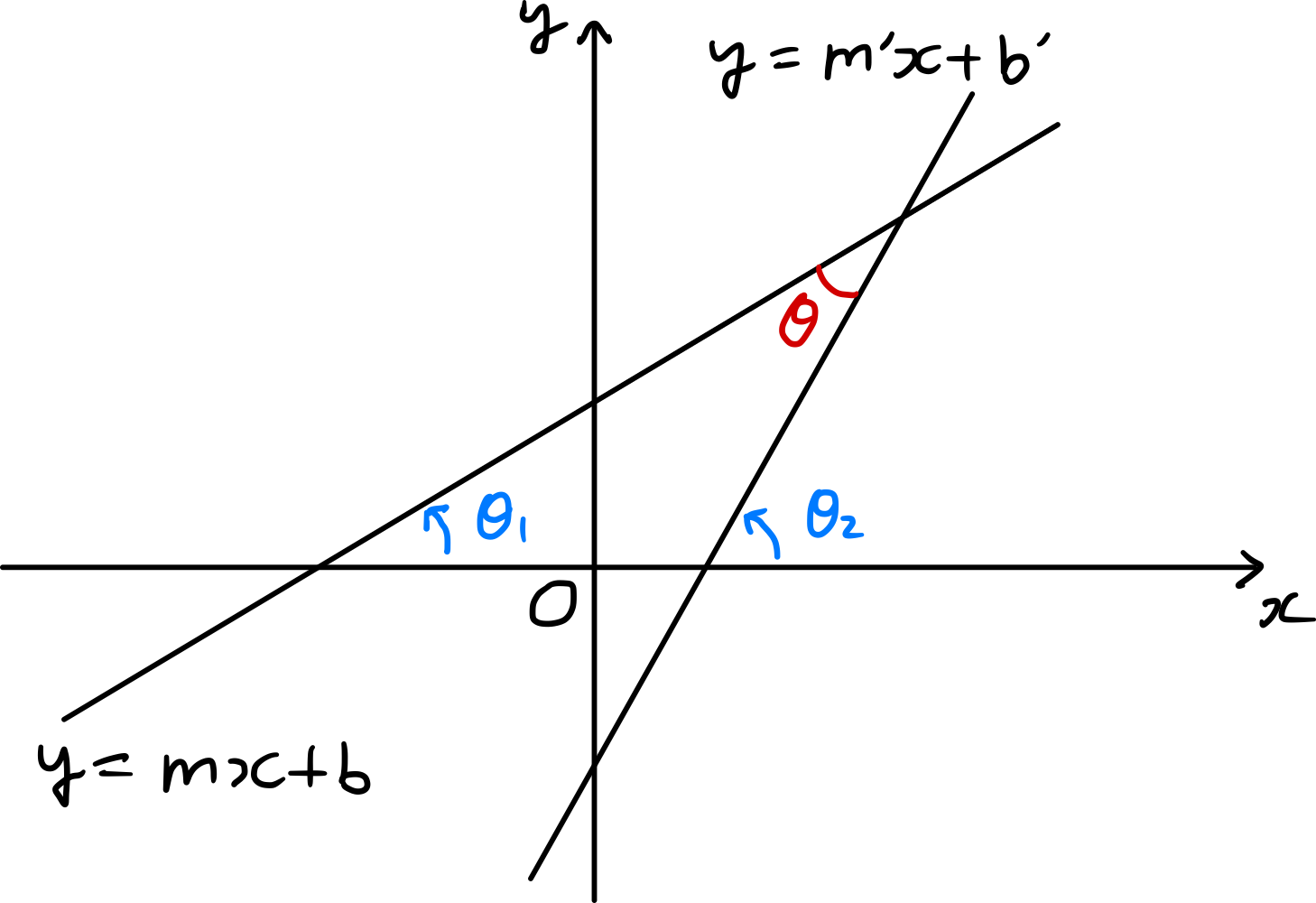En utilisant l’équation ($\ref{eqn:tan_2}$), on peut trouver la taille de l’angle aigu formé par deux droites de pentes données. Si $\theta_{1}$ et $\theta_{2}$ sont les angles formés par les deux droites $y=mx+b$ et $y=m^{\prime} x+b^{\prime}$ avec la direction positive de l’axe $x$ respectivement, alors
Donc, si $\theta$ est la taille de l’angle aigu formé par les deux droites,
\[\tag{11} \begin{align*} \tan{\theta}&=\left\vert \tan{\theta_{2}-\theta_{1}} \right\vert=\left\vert \frac{\tan{\theta_2}-\tan{\theta_1}}{1+\tan{\theta_1}\tan{\theta_2}}\right\vert \\ &=\left\vert \frac{m-m^{\prime}}{1+mm^{\prime}} \right\vert. \end{align*}\]