Teorema de la adición armónica

TL;DR

Teorema de la adición armónica

• \[a\sin \theta + b\cos \theta = \sqrt{a^{2}+b^{2}} \sin(\theta+\alpha)\]

\[(donde,\ \cos \alpha = \frac{a}{\sqrt{a^{2}+b^{2}}},\ \sin \alpha = \frac{b}{\sqrt{a^{2}+b^{2}}})\]

• \[a\sin \theta + b\cos \theta = \sqrt{a^{2}+b^{2}} \cos(\theta-\beta)\]

\[(donde,\ \cos \beta = \frac{b}{\sqrt{a^{2}+b^{2}}},\ \sin \beta = \frac{a}{\sqrt{a^{2}+b^{2}}})\]

Prerrequisitos

• Fórmulas de adición trigonométrica

Teorema de la adición armónica

Para una función $f(\theta) = a \cos \theta + b \sin \theta$ que es una suma de funciones trigonométricas, siempre existen números reales $\alpha$ y $\beta$ que satisfacen $f(\theta)=\sqrt{a^2+b^2} \sin(\theta+\alpha) = \sqrt{a^2+b^2} \cos(\theta-\beta)$.

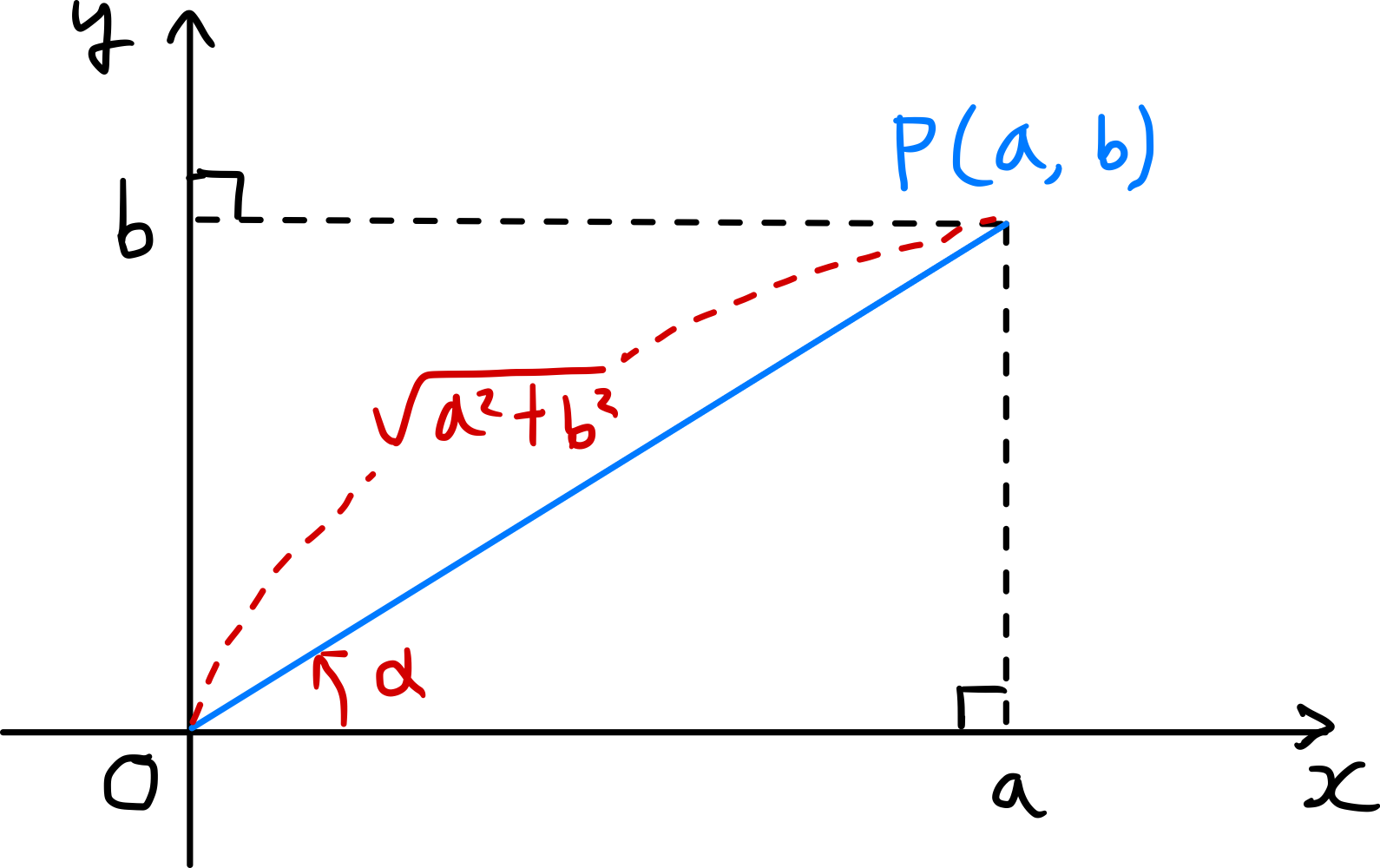
Como se muestra en la figura, si tomamos un punto $P(a,b)$ en el plano de coordenadas y definimos $\alpha$ como el ángulo entre el segmento $\overline{OP}$ y la dirección positiva del eje $x$, entonces

\[\overline{OP} = \sqrt{a^2+b^2}\]

y

\[\cos \alpha = \frac{a}{\sqrt{a^{2} + b^{2}}},\ \sin \alpha = \frac{b}{\sqrt{a^{2} + b^{2}}} \tag{1}\]

En este caso,

\[\begin{align*} a \sin \theta + b \cos \theta &= \sqrt{a^{2}+b^{2}} \left(\frac{a}{\sqrt{a^{2}+b^{2}}}\sin \theta + \frac{b}{\sqrt{a^{2}+b^{2}}}\cos \theta \right) \\ &= \sqrt{a^{2}+b^{2}}(\cos \alpha \sin \theta + \sin \alpha \cos \theta) \\ &= \sqrt{a^{2}+b^{2}} \sin(\theta + \alpha). \tag{2} \end{align*}\]

De manera similar, si tomamos un punto $P^{\prime}(b,a)$ y definimos $\beta$ como el ángulo entre el segmento $\overline{OP^{\prime}}$ y la dirección positiva del eje $x$, obtenemos:

\[a \sin \theta + b \cos \theta = \sqrt{a^{2}+b^{2}}\cos(\theta-\beta). \tag{3}\] \[donde,\ \cos \beta = \frac{b}{\sqrt{a^{2}+b^{2}}},\ \sin \beta = \frac{a}{\sqrt{a^{2}+b^{2}}}.\]

La transformación de una función trigonométrica de la forma $a \sin \theta + b \sin \theta$ en la forma $r\sin(\theta+\alpha)$ o $r\cos(\theta-\beta)$ se denomina adición armónica de funciones trigonométricas.

Ejemplo

Dada la función $f(\theta)=-\sqrt{3}\sin \theta + \cos \left(\theta - \frac{\pi}{3} \right)$, encuentra los valores máximo y mínimo de la función $f(\theta)$ en el intervalo $[0, 2\pi]$.

1. Transformar a la forma $a\sin\theta + b\cos\theta$

Usando las fórmulas de adición trigonométrica, transformamos la función dada:

\[\begin{align*} f(\theta) &= -\sqrt{3}\sin \theta + \cos \left(\theta - \frac{\pi}{3} \right) \\ &= -\sqrt{3}\sin \theta + \left( \cos\theta \cos\frac{\pi}{3} + \sin\theta \sin\frac{\pi}{3} \right) \\ &= -\frac{\sqrt{3}}{2}\sin\theta + \frac{1}{2}\cos\theta . \end{align*}\]

2. Transformar a la forma $r\sin(\theta+\alpha)$

Tomando $a=-\frac{\sqrt{3}}{2}$ y $b=\frac{1}{2}$, tenemos:

\[r = \sqrt{a^2+b^2} = \sqrt{\frac{3}{4}+\frac{1}{4}} = 1\]

Además, existe un único valor real $\alpha$ tal que $0 \leq \alpha<2\pi$, $\cos\alpha = a$ y $\sin\alpha = b$. A partir de los valores trigonométricos de ángulos especiales, podemos determinar que $\alpha = \frac{5}{6}\pi$.

Por lo tanto, la función dada $f(\theta)$ transformada a la forma $r\sin(\theta+\alpha)$ es:

\[f(\theta) = \sin \left(\theta + \frac{5\pi}{6} \right).\]

3. Encontrar los valores máximo y mínimo en el intervalo dado

La función $f(\theta) = \sin \left(\theta + \frac{5\pi}{6} \right)$ es una función periódica con período $2\pi$, y en el intervalo dado tiene un valor máximo de $1$ y un valor mínimo de $-1$.

\[\therefore M=1,\ m=-1\]