Teoremas de adición de funciones trigonométricas
Examinamos las definiciones de las funciones trigonométricas y las relaciones entre ellas, y de ahí derivamos los teoremas de adición de funciones trigonométricas y fórmulas relacionadas.
Definición de funciones trigonométricas
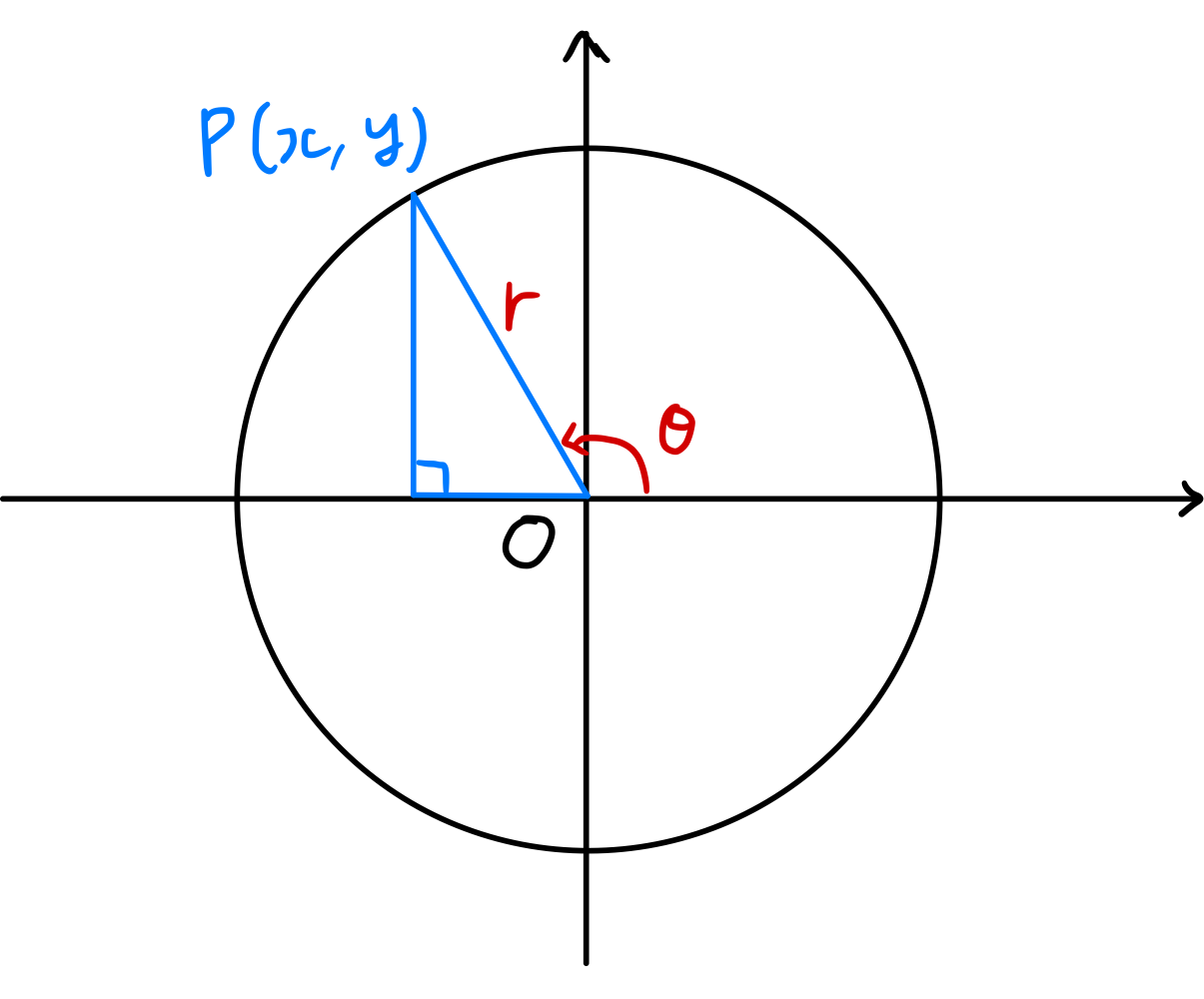Como se muestra en la figura, cuando el tamaño del ángulo formado por el radio vector $\overline{OP}$ y la dirección positiva del eje $x$ es $\theta$, \(\begin{gather}\begin{split} \sin \theta = \frac { y } { r } ,\; \cos \theta = \frac { x } { r } ,\; \tan \theta = \frac { y } { x } \\ \csc \theta = \frac { r } { y } ,\; \sec \theta = \frac { r } { x } ,\; \cot \theta = \frac { x } { y } \end{split}\end{gather}\) se definen así, y colectivamente se denominan funciones trigonométricas.
Relaciones entre funciones trigonométricas
- \[\csc \theta = \frac { 1 } { \sin \theta } ,\; \sec \theta = \frac { 1 } { \cos \theta } ,\; \cot \theta = \frac { 1 } { \tan \theta } \tag{2}\]
- \[\tan \theta = \frac { \sin \theta } { \cos \theta } ,\; \cot \theta = \frac { \cos \theta } { \sin \theta } \tag{3}\]
- \[\tag{4} \begin{gather*} \sin ^ { 2 } \theta + \cos ^ { 2 } \theta = 1 \\ \tan ^ { 2 } \theta + 1 = \sec ^ { 2 } \theta \\ 1 + \cot ^ { 2 } \theta = \csc ^ { 2 } \theta \end{gather*}\]
Teoremas de adición de funciones trigonométricas
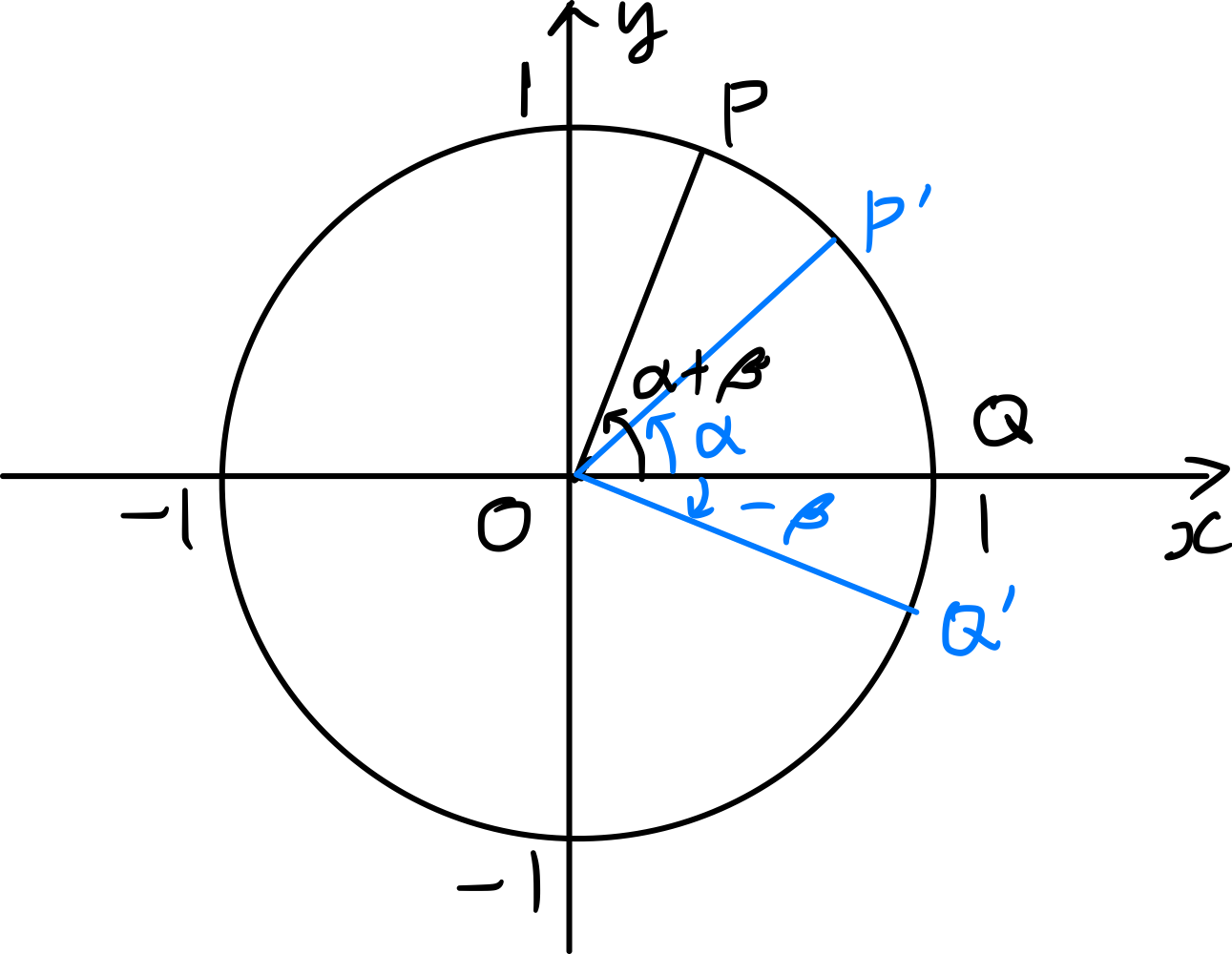Como se muestra en la figura, sean $P, Q, P^{\prime}, Q^{\prime}$ los puntos donde cuatro radios vectores que forman ángulos de $\alpha+\beta,\, 0,\, \alpha,\, -\beta$ con la dirección positiva del eje $x$ intersectan el círculo unitario, respectivamente.
Las coordenadas de los dos puntos $P, Q$ son
\[P(\cos(\alpha+\beta), \sin(\alpha+\beta)),\; Q(1,0)\]por lo tanto
\[\begin{align*} \overline { P^ { \prime } Q^ { \prime } } ^2&= \{ \cos \alpha - \cos ( - \beta ) \} ^ { 2 } + \{ \sin \alpha - \sin ( - \beta ) \} ^ { 2 } \\ &= 2 - 2 \cos \alpha \cos ( - \beta ) - 2 \sin \alpha \sin ( - \beta ) \\ &= 2 - 2 \cos \alpha \cos \beta + 2 \sin \alpha \sin \beta. \end{align*}\]Como $\overline{PQ}=\overline{P^{\prime} Q^{\prime}}$, $2 - 2 \cos ( \alpha + \beta ) = 2 - 2 \cos \alpha \cos \beta + 2 \sin \alpha \sin \beta.$
\[\therefore \cos ( \alpha + \beta ) = \cos \alpha \cos \beta - \sin \alpha \sin \beta. \label{eqn:cos_1} \tag{5}\]Si sustituimos $\beta$ por $-\beta$ en la ecuación anterior y reorganizamos,
\[\cos ( \alpha - \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \label{eqn:cos_2} \tag{6}\]Como $\cos ( \frac { \pi } { 2 } - \theta ) = \sin \theta ,\, \sin ( \frac { \pi } { 2 } - \theta ) = \cos \theta$,
\[\begin{align*} \sin ( \alpha + \beta ) &= \cos ( \frac { \pi } { 2 } - ( \alpha + \beta ) ) = \cos ( ( \frac { \pi } { 2 } - \alpha ) - \beta) \\ &= \cos ( \frac { \pi } { 2 } - x ) \cos \beta + \sin ( \frac { \pi } { 2 } - \alpha ) \sin \beta \\ &= \sin \alpha \cos \beta + \cos \alpha \sin \beta. \end{align*}\] \[\therefore \sin ( \alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta. \label{eqn:sin_1} \tag{7}\]Si sustituimos $\beta$ por $-\beta$ en esta ecuación y reorganizamos,
\[\sin ( \alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta. \label{eqn:sin_2} \tag{8}\]Finalmente,
\[\tan ( \alpha + \beta ) = \frac { \sin ( \alpha + \beta ) } { \cos ( \alpha + \beta ) } = \frac { \sin \alpha \cos \beta + \cos \alpha \sin \beta } { \cos \alpha \cos \beta - \sin \alpha \sin \beta }\]Si dividimos tanto el numerador como el denominador por $\cos{\alpha} \cos{\beta}$ y reorganizamos,
\[\tan ( \alpha + \beta ) = \frac { \tan \alpha + \tan \beta } { 1 - \tan \alpha \tan \beta } \label{eqn:tan_1} \tag{9}\]y si sustituimos $\beta$ por $-\beta$ en esta ecuación y reorganizamos,
\[\tan ( \alpha - \beta ) = \frac { \tan \alpha - \tan \beta } { 1 + \tan \alpha \tan \beta } \label{eqn:tan_2} \tag{10}\]Tamaño del ángulo agudo formado por dos líneas rectas con pendientes dadas
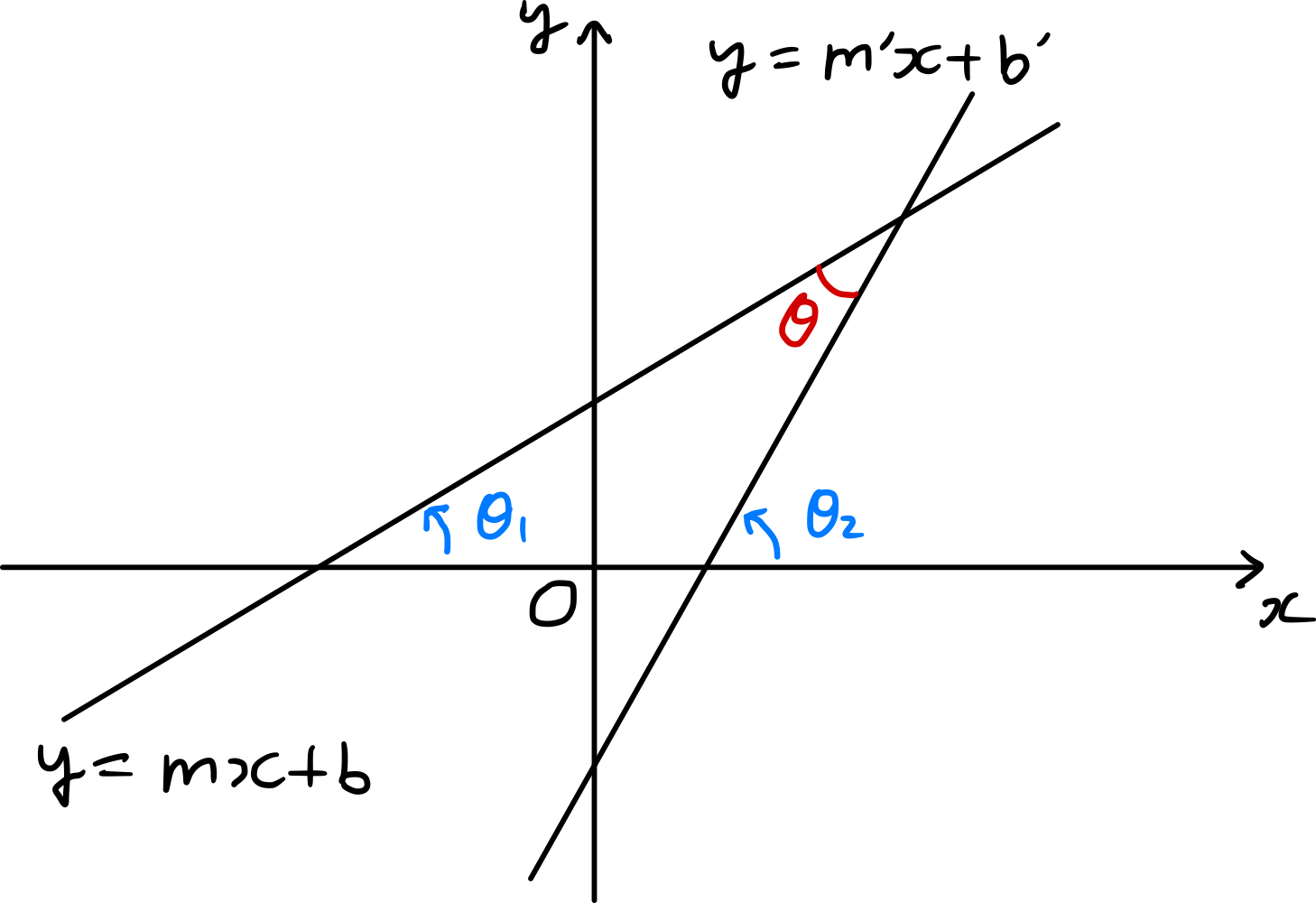Usando la ecuación ($\ref{eqn:tan_2}$), podemos calcular el tamaño del ángulo agudo formado por dos líneas rectas con pendientes dadas. Si $\theta_{1}$ y $\theta_{2}$ son los tamaños de los ángulos formados por las dos líneas rectas $y=mx+b$ y $y=m^{\prime} x+b^{\prime}$ con la dirección positiva del eje $x$ respectivamente,
por lo tanto, si $\theta$ es el tamaño del ángulo agudo formado por las dos líneas rectas,
\[\tag{11} \begin{align*} \tan{\theta}&=\left\vert \tan{\theta_{2}-\theta_{1}} \right\vert=\left\vert \frac{\tan{\theta_2}-\tan{\theta_1}}{1+\tan{\theta_1}\tan{\theta_2}}\right\vert \\ &=\left\vert \frac{m-m^{\prime}}{1+mm^{\prime}} \right\vert. \end{align*}\]