三角函數的合成（Harmonic Addition Theorem）

TL;DR

三角函數的合成（Harmonic Addition Theorem）

• \[a\sin \theta + b\cos \theta = \sqrt{a^{2}+b^{2}} \sin(\theta+\alpha)\]

\[(其中,\ \cos \alpha = \frac{a}{\sqrt{a^{2}+b^{2}}},\ \sin \alpha = \frac{b}{\sqrt{a^{2}+b^{2}}})\]

• \[a\sin \theta + b\cos \theta = \sqrt{a^{2}+b^{2}} \cos(\theta-\beta)\]

\[(其中,\ \cos \beta = \frac{b}{\sqrt{a^{2}+b^{2}}},\ \sin \beta = \frac{a}{\sqrt{a^{2}+b^{2}}})\]

先備知識

• 三角函數的加法定理

三角函數的合成（Harmonic Addition Theorem）

對於形如 $f(\theta) = a \cos \theta + b \sin \theta$ 的三角函數和函數 $f(\theta)$，總存在實數 $\alpha$ 和 $\beta$，使得 $f(\theta)=\sqrt{a^2+b^2} \sin(\theta+\alpha) = \sqrt{a^2+b^2} \cos(\theta-\beta)$。

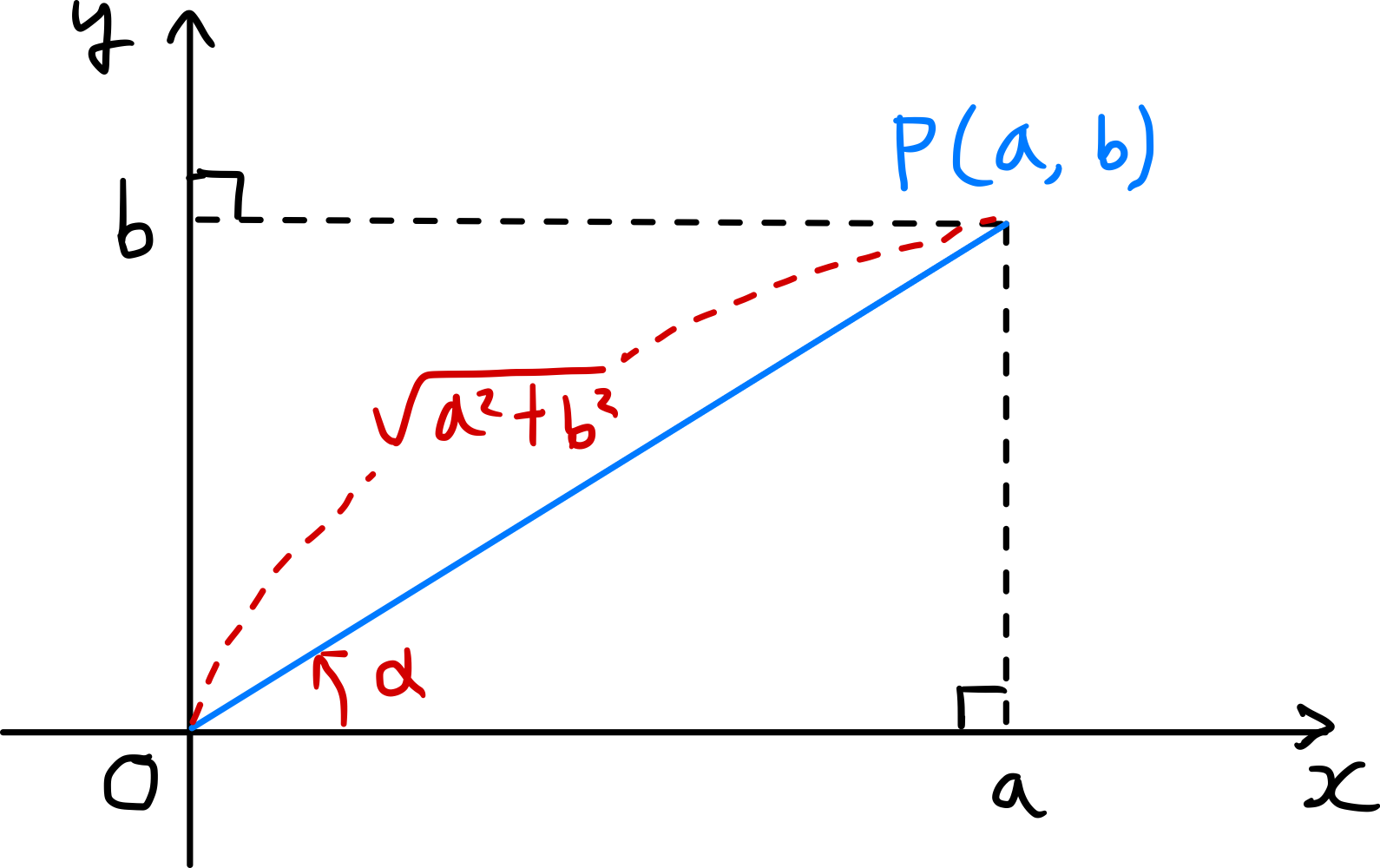
如圖所示，在坐標平面上取點 $P(a,b)$，線段 $\overline{OP}$ 與 $x$ 軸正方向所成的角度大小為 $\alpha$，則

\[\overline{OP} = \sqrt{a^2+b^2}\]

且

\[\cos \alpha = \frac{a}{\sqrt{a^{2} + b^{2}}},\ \sin \alpha = \frac{b}{\sqrt{a^{2} + b^{2}}} \tag{1}\]

此時，

\[\begin{align*} a \sin \theta + b \cos \theta &= \sqrt{a^{2}+b^{2}} \left(\frac{a}{\sqrt{a^{2}+b^{2}}}\sin \theta + \frac{b}{\sqrt{a^{2}+b^{2}}}\cos \theta \right) \\ &= \sqrt{a^{2}+b^{2}}(\cos \alpha \sin \theta + \sin \alpha \cos \theta) \\ &= \sqrt{a^{2}+b^{2}} \sin(\theta + \alpha). \tag{2} \end{align*}\]

同樣的方法，取點 $P^{\prime}(b,a)$，線段 $\overline{OP^{\prime}}$ 與 $x$ 軸正方向所成的角度大小為 $\beta$，則可得：

\[a \sin \theta + b \cos \theta = \sqrt{a^{2}+b^{2}}\cos(\theta-\beta). \tag{3}\] \[其中,\ \cos \beta = \frac{b}{\sqrt{a^{2}+b^{2}}},\ \sin \beta = \frac{a}{\sqrt{a^{2}+b^{2}}}.\]

這種將 $a \sin \theta + b \sin \theta$ 形式的三角函數轉換為 $r\sin(\theta+\alpha)$ 或 $r\cos(\theta-\beta)$ 形式的過程稱為三角函數的合成（Harmonic Addition）。

例題

設函數 $f(\theta)=-\sqrt{3}\sin \theta + \cos \left(\theta - \frac{\pi}{3} \right)$，求函數 $f(\theta)$ 在區間 $[0, 2\pi]$ 上的最大值和最小值。

1. 轉換為 $a\sin\theta + b\cos\theta$ 形式

利用三角函數的加法定理，將給定函數式轉換為：

\[\begin{align*} f(\theta) &= -\sqrt{3}\sin \theta + \cos \left(\theta - \frac{\pi}{3} \right) \\ &= -\sqrt{3}\sin \theta + \left( \cos\theta \cos\frac{\pi}{3} + \sin\theta \sin\frac{\pi}{3} \right) \\ &= -\frac{\sqrt{3}}{2}\sin\theta + \frac{1}{2}\cos\theta . \end{align*}\]

2. 轉換為 $r\sin(\theta+\alpha)$ 形式

令 $a=-\frac{\sqrt{3}}{2}$，$b=\frac{1}{2}$，則

\[r = \sqrt{a^2+b^2} = \sqrt{\frac{3}{4}+\frac{1}{4}} = 1\]

此外，存在唯一的實數 $\alpha$，滿足 $0 \leq \alpha<2\pi$，$\cos\alpha = a$，$\sin\alpha = b$。根據特殊角的三角比值，可知 $\alpha = \frac{5}{6}\pi$。

因此，將給定函數 $f(\theta)$ 轉換為 $r\sin(\theta+\alpha)$ 形式如下：

\[f(\theta) = \sin \left(\theta + \frac{5\pi}{6} \right).\]

3. 求給定區間內的最大值和最小值

函數 $f(\theta) = \sin \left(\theta + \frac{5\pi}{6} \right)$ 是週期為 $2\pi$ 的週期函數，在給定區間內最大值為 $1$，最小值為 $-1$。

\[\therefore M=1,\ m=-1\]