碰撞引起的能量傳遞

TL;DR

• 碰撞時總能量和動量守恆
• 失去所有電子只剩原子核的離子和電子只有動能
• 中性原子和只失去部分電子的離子具有內部能量，隨著勢能的變化可能發生激發（excitation）、去激發（deexcitation）或電離（ionization）
• 根據碰撞前後動能變化的碰撞類型分類：
  • 彈性碰撞（elastic collision）：碰撞前後動能總量保持不變
  • 非彈性碰撞（inelastic collision）：碰撞過程中動能損失
    • 激發（excitation）
    • 電離（ionization）
  • 超彈性碰撞（superelastic collision）：碰撞過程中動能增加
    • 去激發（deexcitation）
• 彈性碰撞的能量傳遞率：
  • 單次碰撞的能量傳遞率：$\zeta_L = \cfrac{4m_1m_2}{(m_1+m_2)^2}\cos^2\theta_2$
  • 每次碰撞的平均能量傳遞率：$\overline{\zeta_L} = \cfrac{4m_1m_2}{(m_1+m_2)^2}\overline{\cos^2\theta_2} = \cfrac{2m_1m_2}{(m_1+m_2)^2}$
    • 當 $m_1 \approx m_2$ 時：$\overline{\zeta_L} \approx \cfrac{1}{2}$，能量傳遞有效，迅速達到熱平衡
    • 當 $m_1 \ll m_2$ 或 $m_1 \gg m_2$ 時：$\overline{\zeta_L} \approx 10^{-5}\sim 10^{-4}$，能量傳遞效率非常低，難以達到熱平衡。這是弱電離電漿中 $T_e \gg T_i \approx T_n$ 電子溫度與離子溫度及中性原子溫度差異很大的原因。
• 非彈性碰撞的能量傳遞率：
  • 單次碰撞的最大內部能量轉換率：$\zeta_L = \cfrac{\Delta U_\text{max}}{\cfrac{1}{2}m_1v_1^2} = \cfrac{m_2}{m_1+m_2}\cos^2\theta_2$
  • 平均最大內部能量轉換率：$\overline{\zeta_L} = \cfrac{m_2}{m_1+m_2}\overline{\cos^2\theta_2} = \cfrac{m_2}{2(m_1+m_2)}$
    • 當 $m_1 \approx m_2$ 時：$\overline{\zeta_L} \approx \cfrac{1}{4}$
    • 當 $m_1 \gg m_2$ 時：$\overline{\zeta_L} \approx 10^{-5}\sim 10^{-4}$
    • 當 $m_1 \ll m_2$ 時：$\overline{\zeta_L} = \cfrac{1}{2}$，最有效地提高碰撞對象（離子或中性原子）的內部能量，使其達到激發態。這是電子引起的電離（電漿生成）、激發（發光）、分子解離（dissociation）（自由基生成）等現象容易發生的原因。

Prerequisites

• 亞原子粒子和原子的組成部分

電漿中的粒子間碰撞

• 碰撞時總能量和動量守恆
• 失去所有電子只剩原子核的離子和電子只有動能
• 中性原子和只失去部分電子的離子具有內部能量，隨著勢能的變化可能發生激發（excitation）、去激發（deexcitation）或電離（ionization）
• 根據碰撞前後動能變化的碰撞類型分類：
  • 彈性碰撞（elastic collision）：碰撞前後動能總量保持不變
  • 非彈性碰撞（inelastic collision）：碰撞過程中動能損失
    • 激發（excitation）
    • 電離（ionization）
  • 超彈性碰撞（superelastic collision）：碰撞過程中動能增加
    • 去激發（deexcitation）

彈性碰撞引起的能量傳遞

單次碰撞的能量傳遞率

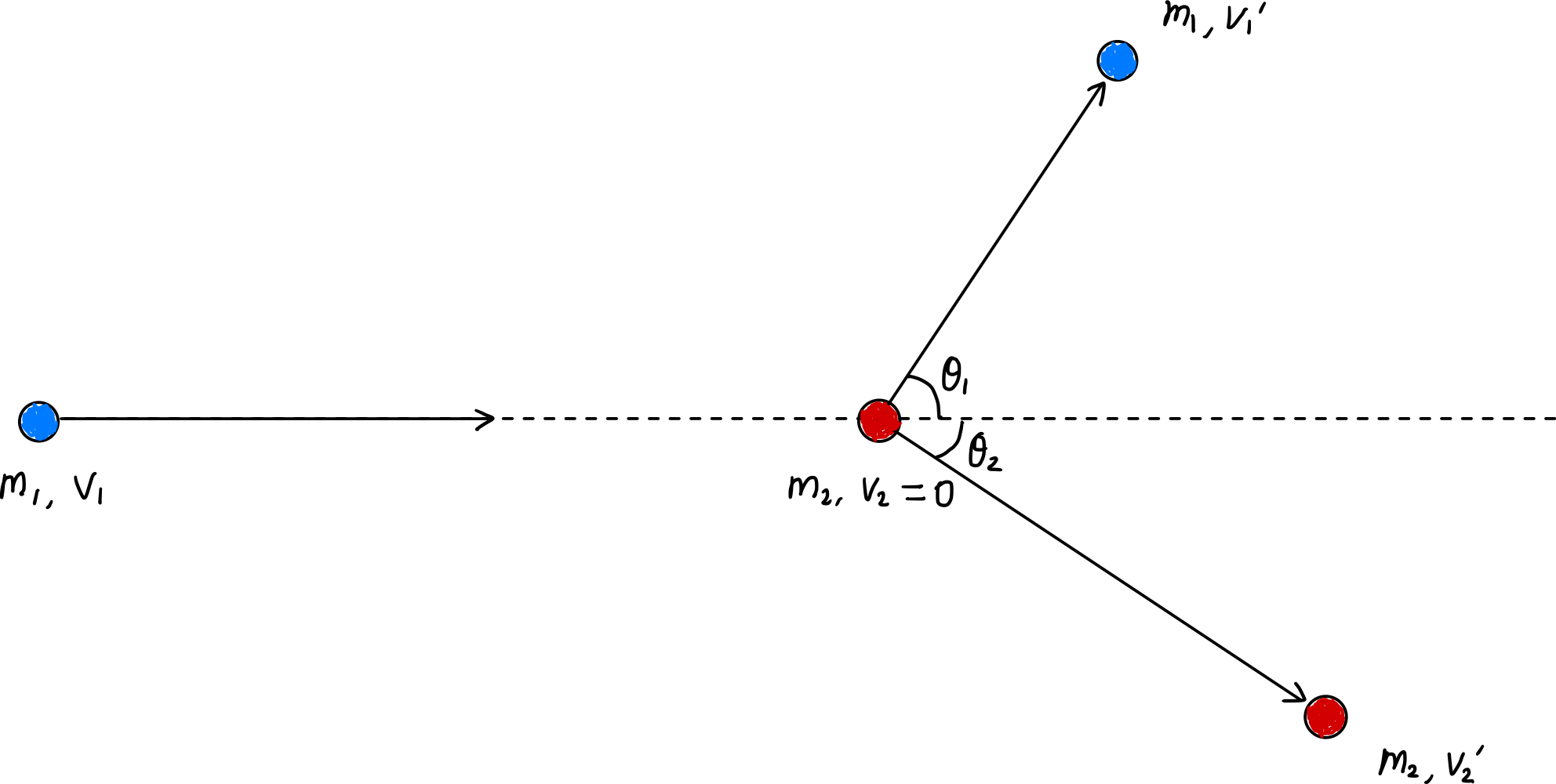
在彈性碰撞中，碰撞前後動量和動能都保持不變。

分別對 $x$ 軸和 $y$ 軸列出動量守恆方程：

\[\begin{gather*} m_1v_1 = m_1v_1^{\prime}\cos\theta_1 + m_2v_2^{\prime}\cos\theta_2, \label{eqn:momentum_conservation_x}\tag{1} \\ m_1v_1^{\prime}\sin\theta_1 = m_2v_2^{\prime}\sin\theta_2 \label{eqn:momentum_conservation_y}\tag{2} \end{gather*}\]

此外，根據能量守恆：

\[\frac{1}{2}m_1v_1^2 = \frac{1}{2}m_1{v_1^{\prime}}^2 + \frac{1}{2}m_2{v_2^{\prime}}^2\] \[v_1^2 = {v_1^{\prime}}^2 + \frac{m_2}{m_1}{v_2^{\prime}}^2 \label{eqn:energy_conservation}\tag{3}\]

從方程 ($\ref{eqn:momentum_conservation_x}$) 得到：

\[m_1 v_1^{\prime} \cos \theta_1 = m_1v_1 - m_2v_2^{\prime} \cos \theta_2 \label{eqn:momentum_conservation_x_2}\tag{4}\]

將方程 ($\ref{eqn:momentum_conservation_y}$) 和 ($\ref{eqn:momentum_conservation_x_2}$) 兩邊平方後相加：

\[\begin{align*} (m_1v_1^{\prime})^2 &= (m_2 v_2^\prime \sin \theta_2)^2 + (m_1 v_1 - m_2 v_2^\prime \cos \theta_2)^2 \\ &= m_1^2 v_1^2 - 2 m_1 m_2 v_1 v_2^\prime \cos \theta_2 + m_2^2 {v_2^\prime}^2 \tag{5} \end{align*}\]

現在兩邊除以 $m_1^2$：

\[{v_1^{\prime}}^2 = v_1^2 - 2 \frac{m_2}{m_1} v_1 v_2^\prime \cos \theta_2 + \left(\frac{m_2}{m_1}\right)^2 {v_2^\prime}^2 \label{eqn:momentum_conservation}\tag{6}\]

將方程 ($\ref{eqn:energy_conservation}$) 代入，可以得到：

\[\begin{gather*} \left( \frac{m_2}{m_1} \right) {v_2^\prime}^2 = 2 \left( \frac{m_2}{m_1} \right) v_1 v_2^\prime \cos \theta_2 - \left( \frac{m_2}{m_1} \right)^2 {v_2^\prime}^2 \\ 2v_1 \cos \theta_2 = \left(\frac{m_1 + m_2}{m_1} \right) v_2^\prime \\ v_2^{\prime} = \frac{2m_1v_1\cos\theta_2}{m_1 + m_2}. \label{eqn:v_2_prime}\tag{7} \end{gather*}\]

由此得到能量傳遞率 $\zeta_L$：

\[\begin{align*} \therefore \zeta_L &= \frac{\cfrac{1}{2}m_2{v_2^\prime}^2}{\cfrac{1}{2}m_1v_1^2} = \frac{m_2}{m_1v_1^2} {\left(\frac{2m_1v_1\cos\theta_2}{m_1 + m_2} \right)}^2 \\ &= \frac{4m_1m_2}{(m_1+m_2)^2}\cos^2\theta_2. \quad \blacksquare \label{eqn:elastic_E_transfer_rate}\tag{8} \end{align*}\]

每次碰撞的平均能量傳遞率

對於從 $0$ 到 $2\pi$ 的角度，$\sin^2{\theta_2}+\cos^2{\theta_2}=1$ 且 $\overline{\sin^2{\theta_2}}=\overline{\cos^2{\theta_2}}$，因此：

\[\begin{align*} \overline{\cos^2{\theta_2}} &= \overline{(1-\sin^2{\theta_2})} = 1 - \overline{\sin^2{\theta_2}} \\ &= 1 - \overline{\cos^2{\theta_2}} \end{align*}\] \[\begin{gather*} 2 \cdot \overline{\cos^2{\theta_2}} = 1 \\ \overline{\cos^2{\theta_2}} = \frac{1}{2}. \end{gather*}\]

將此代入先前得到的方程 ($\ref{eqn:elastic_E_transfer_rate}$)：

\[\overline{\zeta_L} = \frac{4m_1m_2}{(m_1+m_2)^2}\overline{\cos^2\theta_2} = \frac{2m_1m_2}{(m_1+m_2)^2}. \quad \blacksquare \label{eqn:elastic_E_mean_transfer_rate}\tag{9}\]

當 $m_1 \approx m_2$ 時

電子-電子、離子-離子、中性原子-中性原子、離子-中性原子碰撞屬於這種情況。在這種情況下：

\[\overline{\zeta_L} = \frac{2m_1m_2}{(m_1+m_2)^2} \approx \frac{1}{2} \label{eqn:elastic_similar_m}\tag{10}\]

能量傳遞有效，迅速達到熱平衡。

當 $m_1 \ll m_2$ 或 $m_1 \gg m_2$ 時

電子-離子、電子-中性原子、離子-電子、中性原子-電子碰撞屬於這種情況。在這種情況下：

\[\overline{\zeta_L} = \frac{2m_1m_2}{(m_1+m_2)^2} \approx \frac{2m_1}{m_2}\text{ (以 }m_1 \ll m_2 \text{ 為基準)} \approx 10^{-5}\sim 10^{-4} \label{eqn:elastic_different_m}\tag{11}\]

能量傳遞效率非常低，難以達到熱平衡。這是弱電離電漿中 $T_e \gg T_i \approx T_n$ 電子溫度與離子溫度及中性原子溫度差異很大的原因。

非彈性碰撞引起的能量傳遞

單次碰撞的最大內部能量轉換率

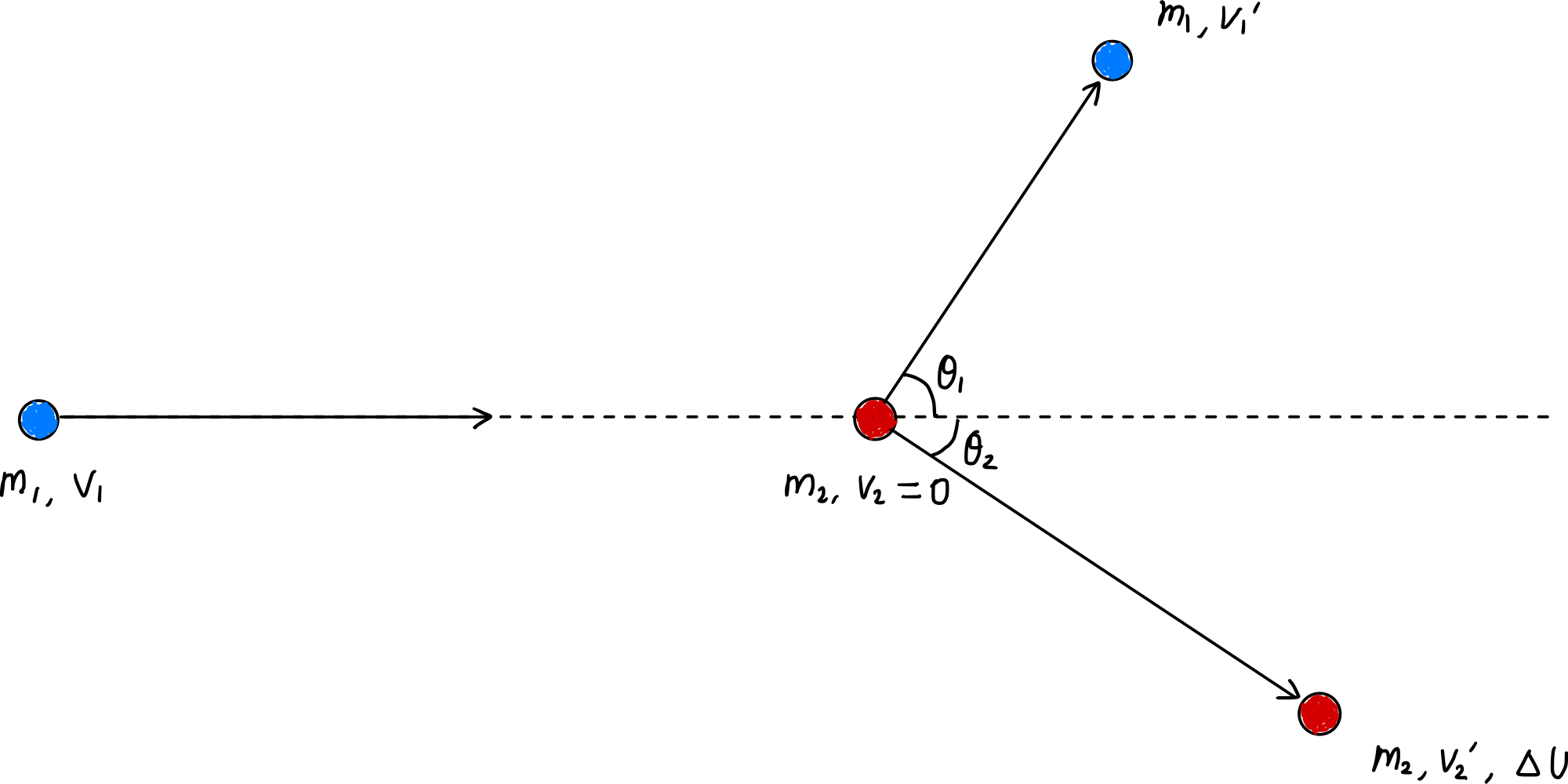
動量守恆（方程 [$\ref{eqn:momentum_conservation}$]）在這種情況下仍然成立，但由於是非彈性碰撞，動能不守恆。此時，非彈性碰撞損失的動能轉換為 $\Delta U$ 的內部能量，因此：

\[\Delta U = \frac{1}{2} m_1 v_1^2 - \left( \frac{1}{2} m_1 {v_1^{\prime}}^2 + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right) \label{eqn:delta_U}\tag{12}\]

現在將方程 ($\ref{eqn:momentum_conservation}$) 代入並整理，得到：

\(\begin{align*} \Delta U &= \frac{1}{2} m_1 v_1^2 - \left[ \frac{1}{2} m_1 \left( v_1^2 - 2 \frac{m_2}{m_1} v_1 v_2^{\prime} \cos \theta_2 + \left( \frac{m_2}{m_1} v_2^{\prime} \right)^2 \right) + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right] \\ &= \frac{1}{2} m_1 v_1^2 - \left[ \frac{1}{2} m_1 v_1^2 - m_2 v_1 v_2^{\prime} \cos \theta_2 + \frac{1}{2} \frac{m_2^2}{m_1} {v_2^{\prime}}^2 + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right] \\ &= m_2 v_1 v_2^{\prime} \cos \theta_2 - \frac{1}{2}m_2{v_2^{\prime}}^2\left(\frac{m_1 + m_2}{m_1}\right) \label{eqn:delta_U_2}\tag{13} \end{align*}\).

對 $\Delta U$ 關於 $v_2^\prime$ 求導，並求該導數值為 $0$ 的極值點及其最大值：

\[\cfrac{d \Delta U}{d v_2^{\prime}} = m_2 v_1 \cos \theta_2 - m_2 v_2^{\prime} \left( \frac{m_1 + m_2}{m_1} \right) = 0 \tag{14}\] \[\begin{gather*} v_2^{\prime} \left( \frac{m_1 + m_2}{m_1} \right) = v_1 \cos \theta_2 \\ v_2^\prime = \frac{m_1v_1\cos\theta_2}{m_1+m_2}. \end{gather*}\] \[\therefore v_2^{\prime} = \frac{m_1v_1\cos\theta_2}{m_1+m_2} \text{時 } \Delta U_\text{max} = \frac{1}{2}\frac{m_1m_2 v_1^2 \cos^2\theta_2}{m_1 + m_2}. \label{eqn:delta_U_max}\tag{15}\]

由此，單次非彈性碰撞可能的動能到內部能量的最大轉換率 $\zeta_L$ 為：

\[\zeta_L = \frac{\Delta U_\text{max}}{\cfrac{1}{2}m_1v_1^2} = \frac{m_2}{m_1+m_2}\cos^2\theta_2. \quad \blacksquare \label{eqn:inelastic_E_transfer_rate}\tag{16}\]

平均最大內部能量轉換率

同樣，將 $\overline{\cos^2{\theta_2}} = \cfrac{1}{2}$ 代入方程 ($\ref{eqn:inelastic_E_transfer_rate}$)，得到：

\[\overline{\zeta_L} = \frac{m_2}{m_1+m_2}\overline{\cos^2\theta_2} = \frac{m_2}{2(m_1+m_2)}. \label{eqn:inelastic_E_mean_transfer_rate}\tag{17}\]

當 $m_1 \approx m_2$ 時

離子-離子、離子-中性原子、中性原子-中性原子碰撞屬於這種情況。

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} = \frac{1}{4}. \label{eqn:inelastic_similar_m}\tag{18}\]

當 $m_1 \gg m_2$ 時

離子-電子、中性原子-電子碰撞屬於這種情況。

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} \approx \frac{m_2}{2m_1} \approx 10^{-5}\sim 10^{-4}. \label{eqn:inelastic_ion_electron}\tag{19}\]

當 $m_1 \ll m_2$ 時

電子-離子、電子-中性原子碰撞屬於這種情況。前兩種情況與彈性碰撞相比沒有太大差異，但這第三種情況顯示了重要的差異。在這種情況下：

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} \approx \frac{m_2}{2m_2} = \frac{1}{2} \label{eqn:inelastic_electron_ion}\tag{20}\]

這是最有效地提高碰撞對象（離子或中性原子）的內部能量，使其達到激發態的情況。這是之後我們將討論的電子引起的電離（電漿生成）、激發（發光）、分子解離（dissociation）（自由基生成）等現象容易發生的原因。