電漿的定義和溫度概念,以及薩哈方程式(Saha equation)
探討電漿定義中「集體行為」的含義,並了解薩哈方程式(Saha equation)。同時釐清電漿物理學中溫度的概念。
TL;DR
\[\frac{n_{i+1}n_e}{n_i} = \frac{2}{\lambda_{\text{th}}^3}\frac{g_{i+1}}{g_i}\exp{\left[-\frac{\epsilon_{i+1}-\epsilon_i}{k_B T}\right]}\]
- 電漿(plasma):由帶電粒子和中性粒子組成的準中性氣體,表現出集體行為
- 電漿的「集體行為(collective behavior)」:
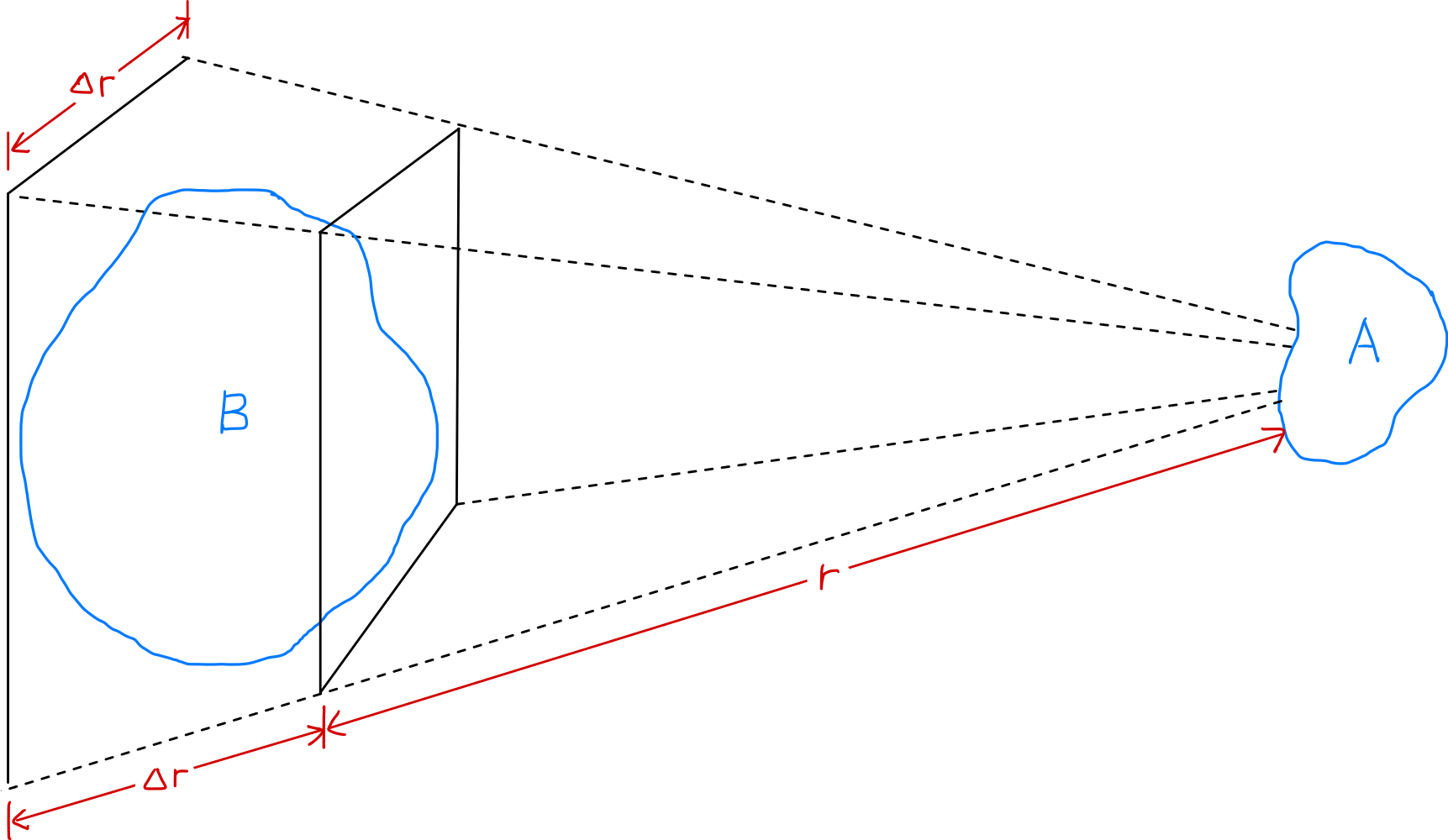
- 電漿中兩個區域 $A$ 和 $B$ 之間的電力隨距離增加而以 $1/r^2$ 減少
- 然而,當給定立體角($\Delta r/r$)保持不變時,可影響 $A$ 的電漿區域 $B$ 的體積以 $r^3$ 增加
- 因此,構成電漿的部分即使在遠距離也能對彼此施加顯著的力
- 薩哈方程式(Saha equation):描述處於熱平衡狀態的氣體的電離狀態與溫度和壓力之間關係的方程式
- 電漿物理學中的溫度概念:
- 在氣體和電漿中,每個粒子的平均動能與溫度密切相關,這兩個量可以互換
- 在電漿物理學中,慣例是使用能量單位 $\mathrm{eV}$ 來表示溫度,即 $kT$ 的值
- $1\mathrm{eV}=11600\mathrm{K}$
- 電漿可以同時具有多個不同的溫度,特別是電子溫度($T_e$)和離子溫度($T_i$)在某些情況下可能會有很大差異
- 低溫電漿 vs. 高溫電漿:
- 電漿溫度:
- 低溫電漿:$T_e \text{(>10,000℃)} \gg T_i \approx T_g \text{(}\sim\text{100℃)}$ $\rightarrow$ 非平衡電漿(non-equilibrium plasma)
- 高溫(熱)電漿:$T_e \approx T_i \approx T_g \text{(>10,000℃)}$ $\rightarrow$ 平衡電漿(equilibrium plasma)
- 電漿密度:
- 低溫電漿:$n_g \gg n_i \approx n_e$ $\rightarrow$ 電離比率小,大部分以中性粒子存在
- 高溫(熱)電漿:$n_g \approx n_i \approx n_e $ $\rightarrow$ 電離比率大
- 電漿的熱容量:
- 低溫電漿:雖然電子溫度高,但密度低,大部分是相對低溫的中性粒子,因此熱容量小,不熱
- 高溫(熱)電漿:電子、離子、中性粒子的溫度都高,因此熱容量大,很熱
Prerequisites
- 亞原子粒子和原子的組成元素
- 麥克斯韋-玻爾茲曼分布(統計力學)
- 質量和能量、粒子和波
- 對稱性和守恆定律(量子力學)、簡併(degeneracy)
電漿的定義
通常在針對非專業人士解釋電漿的文章中,會將電漿定義如下:
將氣體加熱到超高溫狀態,使其組成原子分離成電子和正離子而電離,從而獲得的繼固體、液體、氣體之後的物質第四態
這並非錯誤的說法,韓國核融合能源研究院(Korea Institute of Fusion Energy)網站也是如此介紹的。 這也是搜尋電漿時容易接觸到的普及定義。
雖然上述表述確實正確,但並不能稱為嚴格的定義。我們周圍常溫常壓環境中的氣體也有極小比例的電離,但我們並不稱之為電漿。將氯化鈉等離子化合物溶解在水中時,會分離成帶電的離子,但這種溶液也不是電漿。 換句話說,電漿確實是物質的電離狀態,但並非所有電離的物質都可稱為電漿。
更嚴格地說,電漿可以定義如下:
電漿是由帶電粒子和中性粒子組成的準中性氣體,表現出集體行為。
A plasma is a quasineutral gas of charged and neutral particles which exhibits collective behavior.by Fransis F. Chen
「準中性(quasineutrality)」的含義將在後續討論德拜屏蔽(Debye shielding)時探討。這裡我們來看看電漿的「集體行為(collective behavior)」是什麼意思。
電漿的集體行為
在由中性粒子組成的非電離氣體中,每個氣體分子都是電中性的,因此淨電磁力為 $0$,重力的影響也可以忽略。分子在與其他分子碰撞之前不受干擾地運動,分子間的碰撞決定了粒子的運動。即使部分粒子電離帶電,由於整個氣體中電離粒子的比例非常低,這些帶電粒子的電力影響隨距離以 $1/r^2$ 衰減,無法傳播到遠處。
然而,在含有大量帶電粒子的電漿中,情況完全不同。帶電粒子的移動可能導致正電荷或負電荷的局部集中,從而產生電場。此外,電荷的移動會產生電流,電流又會產生磁場。這些電場和磁場可以在沒有粒子碰撞的情況下影響到遠處的其他粒子。
讓我們來看看兩個略帶電荷的電漿區域 $A$ 和 $B$ 之間的電力強度如何隨距離 $r$ 變化。根據庫倫定律,$A$ 和 $B$ 之間的電力(Coulomb force)隨距離增加而以 $1/r^2$ 減少。然而,當給定立體角($\Delta r/r$)保持不變時,可影響 $A$ 的電漿區域 $B$ 的體積以 $r^3$ 增加。因此,構成電漿的部分即使在遠距離也能對彼此施加顯著的力。這種遠距作用的電力使電漿能夠表現出多種運動模式,也是電漿物理(plasma physics)作為一個獨立學科領域存在的原因。「集體行為(collective behavior)」意味著某一區域的運動不僅受到該區域的局部條件影響,還受到遠處其他區域電漿狀態的影響。
薩哈方程式(Saha equation)
薩哈方程式(Saha equation)是描述處於熱平衡狀態的氣體的電離狀態與溫度和壓力之間關係的方程式,由印度天體物理學家梅格納德·薩哈(Meghnad Saha)提出。
\[\frac{n_{i+1}n_e}{n_i} = \frac{2}{\lambda_{\text{th}}^3}\frac{g_{i+1}}{g_i}\exp{\left[-\frac{\epsilon_{i+1}-\epsilon_i}{k_B T}\right]} \label{eqn:saha_eqn}\tag{1}\]- $n_i$:$i$價正離子(失去 $i$ 個電子的正離子)的密度
- $g_i$:$i$價正離子的態簡併度(degeneracy)
- $\epsilon_i$:從中性原子中移除 $i$ 個電子以產生 $i$價正離子所需的能量
- $\epsilon_{i+1}-\epsilon_i$:$(i+1)$次電離能
- $n_e$:電子密度
- $k_B$:玻爾茲曼常數
- $\lambda_{\text{th}}$:熱德布羅意波長(在給定溫度下氣體中電子的平均德布羅意波長)
- $m_e$:電子質量
- $T$:氣體溫度
如果只有一階電離很重要,可以忽略二價以上正離子的產生,那麼可以設 $n_1=n_i=n_e$,$n_0=n_n$,$U_i = \epsilon = \epsilon_1$,$i=0$,將方程式簡化如下:
\[\begin{align*} \frac{n_i^2}{n_n} &= \frac{2}{\lambda_{th}^3}\frac{g_1}{g_0}\exp{\left[-\frac{\epsilon}{k_B T} \right]} \label{eqn:saha_eqn_approx}\tag{3}\\ &= 2\left(\frac{2\pi m_e k_B T}{h^2}\right)^{3/2}\frac{g_1}{g_0}e^{-U_i/{k_B T}} \\ &= 2\frac{g_1}{g_0}\left(\frac{2\pi m_e k_B}{h^2}\right)^{3/2}T^{3/2}e^{-U_i/{k_B T}}. \label{eqn:saha_eqn_approx_2}\tag{4} \end{align*}\]常溫常壓環境下空氣(氮氣)的電離比率
在上述方程式中,$2 \cfrac{g_1}{g_0}$ 的值因氣體成分而異,但在許多情況下,這個值的數量級(order of magnitude)為 $1$。因此,可以大致近似如下:
\[\frac{n_i^2}{n_n} \approx \left(\frac{2\pi m_e k_B}{h^2}\right)^{3/2} T^{3/2} e^{-U_i/{k_B T}}.\]在 SI 單位制中,基本常數 $m_e$、$k_B$、$h$ 的值分別為:
- $m_e \approx 9.11 \times 10^{-31} \mathrm{kg}$
- $k_B \approx 1.38 \times 10^{-23} \mathrm{J/K}$
- $h \approx 6.63 \times 10^{-34} \mathrm{J \cdot s}$
將這些值代入上述方程式,得到:
\[\frac{n_i^2}{n_n} \approx 2.4 \times 10^{21}\ T^{3/2} e^{-U_i/{k_B T}}. \label{eqn:fractional_ionization}\tag{5}\]由此,對於常溫常壓環境($n_n \approx 3 \times 10^{25} \mathrm{m^{-3}}$,$T\approx 300\mathrm{K}$)下的氮氣($U_i \approx 14.5\mathrm{eV} \approx 2.32 \times 10^{-18}\mathrm{J}$),計算電離比率 $n_i/(n_n + n_i) \approx n_i/n_n$ 的近似值:
\[\frac{n_i}{n_n} \approx 10^{-122}\]可以看出這是一個極低的比率。這就是為什麼在宇宙環境中與地表和海平面附近的大氣環境不同,我們在自然狀態下幾乎無法接觸到電漿的原因。
電漿物理學中的溫度概念
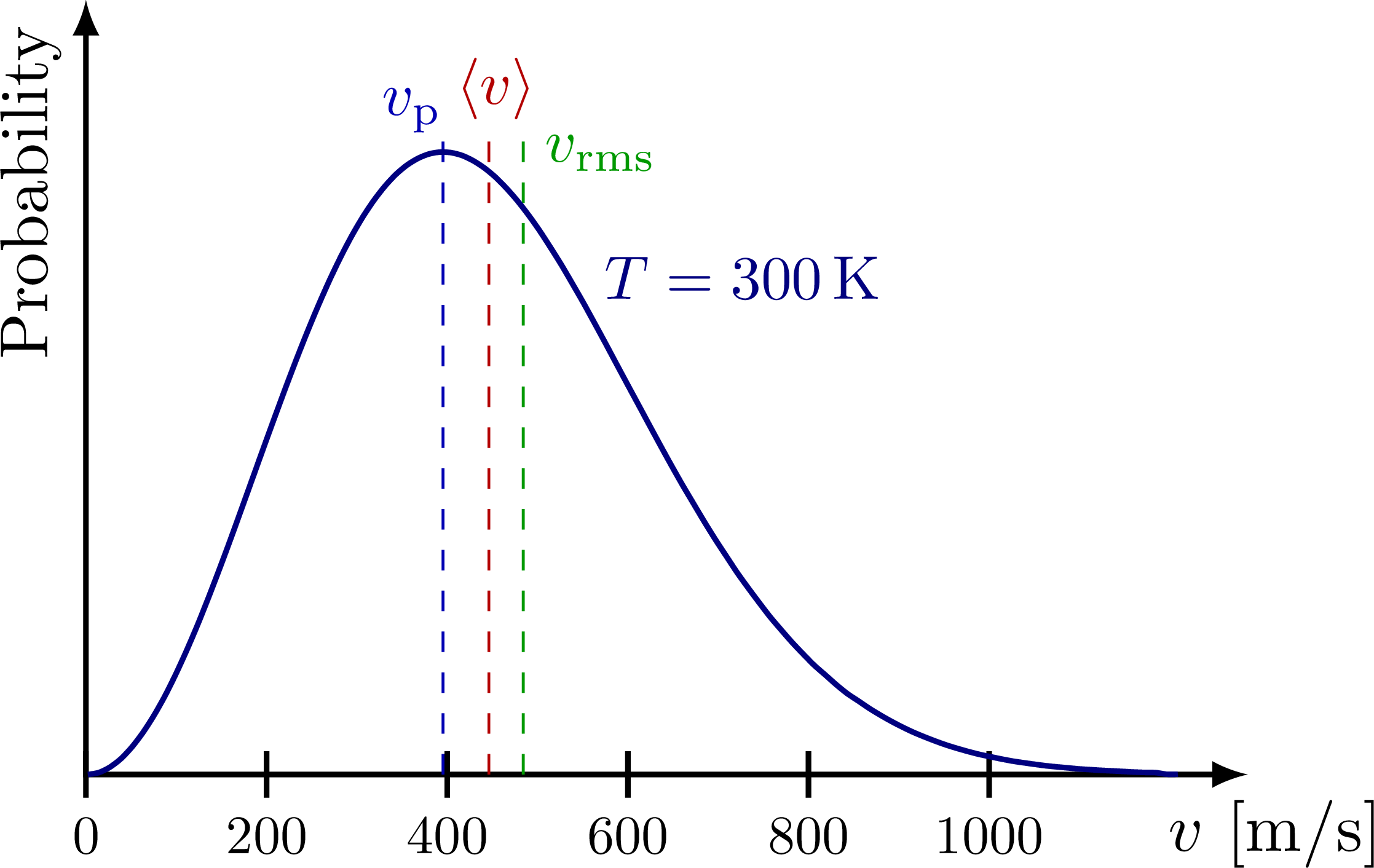
處於熱平衡狀態的氣體中粒子的速度通常遵循以下麥克斯韋-玻爾茲曼分布(Maxwell–Boltzmann distribution):
\[f(v) = \left(\frac{m}{2\pi k_B T} \right)^{3/2} 4\pi v^2 \exp{\left(-\frac{mv^2}{2k_B T} \right)} \label{eqn:maxwell_boltzmann_dist}\tag{6}\]圖片來源
- 作者:TikZ.net author Izaak Neutelings
- 授權:CC BY-SA 4.0
- 最可能速度(most probable speed):$v_p = \sqrt{\cfrac{2k_B T}{m}}$
- 平均速度(mean speed):$\langle v \rangle = \sqrt{\cfrac{8k_B T}{\pi m}}$
- 均方根速度(RMS speed):$v_{rms} = \sqrt{\langle v^2 \rangle} = \sqrt{\cfrac{3k_B T}{m}}$
在溫度 $T$ 下,每個粒子的平均動能為 $\cfrac{1}{2}m\langle v^2 \rangle = \cfrac{1}{2}mv_{rms}^2 = \cfrac{3}{2}k_B T$(基於自由度 $3$),僅由溫度決定。這樣,在氣體和電漿中,每個粒子的平均動能與溫度密切相關,這兩個量可以互換,因此在電漿物理學中,慣例是使用能量單位 $\mathrm{eV}$ 來表示溫度。為避免維度混淆,使用 $kT$ 的值而不是平均動能 $\langle E_k \rangle$ 來表示溫度。
當 $kT=1\mathrm{eV}$ 時,對應的溫度 $T$ 為:
\[\begin{align*} T\mathrm{[K]} &= \frac{1.6 \times 10^{-19}\mathrm{[J]}}{1.38 \times 10^{-23}\mathrm{[J/K]}} \\ &= 11600\mathrm{[K]} \end{align*} \label{eqn:temp_conv_factor}\tag{7}\]因此,在電漿物理學中表示溫度時,$1\mathrm{eV}=11600\mathrm{K}$。 例如:溫度為 $2\mathrm{eV}$ 的電漿的 $kT$ 值為 $2\mathrm{eV}$,每個粒子的平均動能為 $\cfrac{3}{2}kT=3\mathrm{eV}$。
此外,電漿可以同時具有多個溫度。在電漿中,離子之間的碰撞或電子之間的碰撞頻率大於電子和離子之間的碰撞頻率,因此電子和離子可以分別在不同的溫度(電子溫度 $T_e$ 和離子溫度 $T_i$)下達到熱平衡,形成各自的麥克斯韋-玻爾茲曼分布,在某些情況下,電子溫度和離子溫度可能會有很大差異。甚至,當外部施加磁場 $\vec{B}$ 時,同種粒子(例如離子)根據其運動方向是平行還是垂直於磁場,所受到的洛倫茲力(Lorentz force)大小不同,因此可能具有不同的溫度 $T_\perp$ 和 $T_\parallel$。
溫度、壓力和密度之間的關係
根據理想氣體定律:
\[PV = \left(\frac{N}{N_A}\right)RT = NkT \label{eqn:ideal_gas_law}\tag{8}\]由此得出:
\[\begin{gather*} P = \frac{NkT}{V} = nkT, \\ n = \frac{P}{kT} \end{gather*} \label{eqn:relation_between_T_P_n}\tag{9}\]也就是說,電漿的密度與溫度($kT$)成反比,與壓力($P$)成正比。
電漿的分類:低溫電漿 vs. 高溫電漿
| 低溫非熱電漿 (冷電漿) | 低溫熱電漿 (冷電漿) | 高溫電漿 (熱電漿) |
|---|---|---|
| $T_i \approx T \approx 300 \mathrm{K}$ $T_i \ll T_e \leqslant 10^5 \mathrm{K}$ | $T_i \approx T_e \approx T < 2 \times 10^4 \mathrm{K}$ | $T_i \approx T_e > 10^6 \mathrm{K}$ |
| 低壓($\sim 100\mathrm{Pa}$) 輝光放電和電弧放電 | $100\mathrm{kPa}$($1\mathrm{atm}$)下的電弧放電 | 動力學電漿、核融合電漿 |
電漿溫度
將電子溫度記為 $T_e$,離子溫度記為 $T_i$,中性粒子溫度記為 $T_g$,則:
- 低溫電漿:$T_e \mathrm{(>10,000 K)} \gg T_i \approx T_g \mathrm{(\sim 100 K)}$ $\rightarrow$ 非平衡電漿(non-equilibrium plasma)
- 高溫(熱)電漿:$T_e \approx T_i \approx T_g \mathrm{(>10,000 K)}$ $\rightarrow$ 平衡電漿(equilibrium plasma)
電漿密度
將電子密度記為 $n_e$,離子密度記為 $n_i$,中性粒子密度記為 $n_g$,則:
- 低溫電漿:$n_g \gg n_i \approx n_e$ $\rightarrow$ 電離比率小,大部分以中性粒子存在
- 高溫(熱)電漿:$n_g \approx n_i \approx n_e $ $\rightarrow$ 電離比率大
電漿的熱容量(有多熱?)
- 低溫電漿:雖然電子溫度高,但密度低,大部分是相對低溫的中性粒子,因此熱容量小,不熱
- 高溫(熱)電漿:電子、離子、中性粒子的溫度都高,因此熱容量大,很熱