諧振子(The Harmonic Oscillator)的解析解法
建立量子力學中調和振盪子的薛丁格方程,並探討該方程的解析解法。引入無量綱變數 𝜉 來求解方程,並使用厄米多項式表示任意規範化的定態。
TL;DR
\[\begin{gather*} \psi(\xi) = h(\xi)e^{-\xi^2/2} \quad \text{(其中 }\lim_{\xi\to\infty}h(\xi)=A\text{)}, \\ \frac{d^2h}{d\xi^2}-2\xi\frac{dh}{d\xi}+(K-1)h = 0 \end{gather*}\]
- 如果振幅足夠小,任何振動都可以近似為簡諧振動(simple harmonic oscillation),因此簡諧振動在物理學中具有重要意義
- 調和振盪子:$V(x) = \cfrac{1}{2}kx^2 = \cfrac{1}{2}m\omega^2 x^2$
- 引入無量綱變數 $\xi$ 和以 $\cfrac{1}{2}\hbar\omega$ 為單位的能量 $K$:
- $\xi \equiv \sqrt{\cfrac{m\omega}{\hbar}}x$
- $K \equiv \cfrac{2E}{\hbar\omega}$
- $ \cfrac{d^2\psi}{d\xi^2} = \left(\xi^2-K \right)\psi $
- 當 $|\xi|^2 \to \infty$ 時,物理上允許的漸近解為 $\psi(\xi) \to Ae^{-\xi^2/2}$,因此,
\[a_{j+2} = \frac{(2j+1-K)}{(j+1)(j+2)}a_j\]
- 將上述方程的解表示為級數形式 $ h(\xi) = a_0 + a_1\xi + a_2\xi^2 + \cdots = \sum_{j=0}^{\infty}a_j\xi^j$,則
\[h_n(\xi) = \begin{cases} a_0 H_n(\xi), & n=2k & (k=0,1,2,\dots) \\ a_1 H_n(\xi), & n=2k+1 & (k=0,1,2,\dots) \end{cases}\]
- 為了使這個解能夠規範化,級數 $\sum a_j$ 必須是有限的,即存在一個”最大”的 $j$ 值 $n\in \mathbb{N}$,使得當 $j>n$ 時 $a_j=0$,因此
- $ K = 2n + 1 $
- $ E_n = \left(n+\cfrac{1}{2} \right)\hbar\omega, \quad n=0,1,2,\dots $
- 一般來說,$h_n(\xi)$ 是 $\xi$ 的 $n$ 次多項式,其中除了前面的係數($a_0$ 或 $a_1$)外,其餘部分稱為厄米多項式(Hermite polynomials) $H_n(\xi)$
\[\psi_n(x) = \left(\frac{m\omega}{\pi\hbar} \right)^{1/4} \frac{1}{\sqrt{2^n n!}}H_n(\xi)e^{-\xi^2/2}\]
- 調和振盪子的規範化定態:
- 量子振盪子的特徵
- 本徵函數交替出現偶函數和奇函數
- 在經典力學上不可能存在的區域(大於給定 $E$ 的經典振幅的 $x$)也有非零的概率被發現,雖然概率很低,但粒子可能存在
- 對於所有奇數 $n$ 的定態,在中心處發現粒子的概率為 $0$
- $n$ 越大,越接近經典振盪子
Prerequisites
模型設置
關於經典力學中調和振盪子的描述方式以及調和振盪子問題的重要性,請參考前文。
量子力學中的調和振盪子
量子力學的調和振盪子問題是解決勢能為
\[V(x) = \frac{1}{2}m\omega^2 x^2 \label{eqn: potential_omega}\tag{1}\]的薛丁格方程。調和振盪子的與時間無關的薛丁格方程為
\[-\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2} + \frac{1}{2}m\omega^2x^2\psi = E\psi \label{eqn:t_independent_schrodinger_eqn}\tag{2}\]解決這個問題有兩種完全不同的方法。一種是使用冪級數(power series)的解析方法(analytic method),另一種是使用階梯運算子(ladder operators)的代數方法(algebraic method)。代數方法更快速簡單,但學習使用冪級數的解析解法也很有必要。我們之前已經討論過代數解法,這裡我們將討論解析解法。
薛丁格方程的變形
引入無量綱變數
\[\xi \equiv \sqrt{\frac{m\omega}{\hbar}}x \label{eqn:xi}\tag{3}\]則與時間無關的薛丁格方程($\ref{eqn:t_independent_schrodinger_eqn}$)可以簡化為:
\[\frac{d^2\psi}{d\xi^2} = \left(\xi^2-K \right)\psi. \label{eqn:schrodinger_eqn_with_xi}\tag{4}\]這裡 $K$ 是以 $\cfrac{1}{2}\hbar\omega$ 為單位的能量:
\[K \equiv \frac{2E}{\hbar\omega}. \label{eqn:K}\tag{5}\]現在我們需要解這個重寫的方程($\ref{eqn:schrodinger_eqn_with_xi}$)。首先,對於非常大的 $\xi$(即非常大的 $x$),$\xi^2 \gg K$,因此
\[\frac{d^2\psi}{d\xi^2} \approx \xi^2\psi \label{eqn:schrodinger_eqn_approx}\tag{6}\]這個方程的近似解為
\[\psi(\xi) \approx Ae^{-\xi^2/2} + Be^{\xi^2/2} \label{eqn:psi_approx}\tag{7}\]然而,$B$ 項在 $|x|\to \infty$ 時發散,無法規範化,因此物理上允許的漸近解為
\[\psi(\xi) \to Ae^{-\xi^2/2} \label{eqn:psi_asymp}\tag{8}\]現在,我們將指數部分分離出來,寫成
\[\psi(\xi) = h(\xi)e^{-\xi^2/2} \quad \text{(其中 }\lim_{\xi\to\infty}h(\xi)=A\text{)} \label{eqn:psi_and_h}\tag{9}\]我們在推導過程中使用近似法找到漸近解的形式,以發現指數項 $e^{-\xi^2/2}$,但通過這種方法得到的式($\ref{eqn:psi_and_h}$)不是近似式,而是精確式。這種分離漸近形式的方法是解微分方程時使用冪級數的標準第一步。
對式($\ref{eqn:psi_and_h}$)進行微分,得到 $\cfrac{d\psi}{d\xi}$ 和 $\cfrac{d^2\psi}{d\xi^2}$:
\[\begin{gather*} \frac{d\psi}{d\xi} = \left(\frac{dh}{d\xi}-\xi h \right)e^{-\xi^2/2}, \\ \frac{d^2\psi}{d\xi^2} = \left(\frac{d^2h}{d\xi^2}-2\xi\frac{dh}{d\xi}+(\xi^2-1)h \right)e^{-\xi^2/2} \end{gather*}\]將這些代入薛丁格方程($\ref{eqn:schrodinger_eqn_with_xi}$),得到
\[\frac{d^2h}{d\xi^2}-2\xi\frac{dh}{d\xi}+(K-1)h = 0 \label{eqn:schrodinger_eqn_with_h}\tag{10}\]冪級數展開
根據泰勒定理(Taylor’s theorem),任何光滑變化的函數都可以表示為冪級數,因此我們可以將式($\ref{eqn:schrodinger_eqn_with_h}$)的解表示為 $\xi$ 的級數形式:
\[h(\xi) = a_0 + a_1\xi + a_2\xi^2 + \cdots = \sum_{j=0}^{\infty}a_j\xi^j \label{eqn:h_series_exp}\tag{11}\]對這個級數的每一項進行微分,得到以下兩個式子:
\[\begin{gather*} \frac{dh}{d\xi} = a_1 + 2a_2\xi + 3a_3\xi^2 + \cdots = \sum_{j=0}^{\infty}ja_j\xi^{j-1}, \\ \frac{d^2 h}{d\xi^2} = 2a_2 + 2\cdot3a_3\xi + 3\cdot4a_4\xi^2 + \cdots = \sum_{j=0}^{\infty} (j+1)(j+2)a_{j+2}\xi^j. \end{gather*}\]將這兩個式子代入薛丁格方程(式 [$\ref{eqn:schrodinger_eqn_with_h}$]),得到:
\[\sum_{j=0}^{\infty}[(j+1)(j+2)a_{j+2} - 2ja_j + (K-1)a_j]\xi^j = 0. \label{eqn:schrodinger_eqn_power_series}\tag{12}\]根據冪級數展開的唯一性,$\xi$ 的每一次方的係數必須為 0,因此
\[(j+1)(j+2)a_{j+2} - 2ja_j + (K-1)a_j = 0\] \[\therefore a_{j+2} = \frac{(2j+1-K)}{(j+1)(j+2)}a_j. \label{eqn:recursion_formula}\tag{13}\]這個遞迴公式(recursion formula)等同於薛丁格方程。給定兩個任意常數 $a_0$ 和 $a_1$,我們就可以求出解 $h(\xi)$ 的所有項的係數。
然而,並非所有這樣得到的解都可以規範化。如果級數 $\sum a_j$ 是無窮級數(即 $\lim_{j\to\infty} a_j\neq0$),對於非常大的 $j$,上述遞迴公式近似為
\[a_{j+2} \approx \frac{2}{j}a_j\]這個方程的近似解為
\[a_j \approx \frac{C}{(j/2)!} \quad \text{(}C\text{為任意常數)}\]在這種情況下,對於大的 $\xi$ 值,高次項將佔主導地位,
\[h(\xi) \approx C\sum\frac{1}{(j/2)!}\xi^j \approx C\sum\frac{1}{j!}\xi^{2j} \approx Ce^{\xi^2}\]如果 $h(\xi)$ 呈 $Ce^{\xi^2}$ 的形式,則式($\ref{eqn:psi_and_h}$)中的 $\psi(\xi)$ 將呈 $Ce^{\xi^2/2}$ 的形式,在 $\xi \to \infty$ 時發散。這對應於式($\ref{eqn:psi_approx}$)中 $A=0, B\neq0$ 的無法規範化的解。
因此,級數 $\sum a_j$ 必須是有限的。必須存在一個”最大”的 $j$ 值 $n\in \mathbb{N}$,使得當 $j>n$ 時 $a_j=0$。為了實現這一點,對於非零的 $a_n$,必須有 $a_{n+2}=0$。根據式($\ref{eqn:recursion_formula}$),這要求
\[K = 2n + 1\]將此代入式($\ref{eqn:K}$),我們得到物理上允許的能量
\[E_n = \left(n+\frac{1}{2} \right)\hbar\omega, \quad n=0,1,2,\dots \label{eqn:E_n}\tag{14}\]這與調和振盪子的代數解法中的式(21)得到的能量量子化條件完全一致,儘管我們使用了完全不同的方法。
厄米多項式(Hermite polynomials)$H_n(\xi)$ 和定態 $\psi_n(x)$
厄米多項式 $H_n$
一般來說,$h_n(\xi)$ 是 $\xi$ 的 $n$ 次多項式,當 $n$ 為偶數時只包含偶數次方項,當 $n$ 為奇數時只包含奇數次方項。這裡,除了前面的係數($a_0$ 或 $a_1$)外,其餘部分稱為厄米多項式(Hermite polynomials) $H_n(\xi)$。
\[h_n(\xi) = \begin{cases} a_0 H_n(\xi), & n=2k & (k=0,1,2,\dots) \\ a_1 H_n(\xi), & n=2k+1 & (k=0,1,2,\dots) \end{cases}\]傳統上,我們任意地將 $H_n$ 的最高次項係數設為 $2^n$。
以下是前幾個厄米多項式:
\[\begin{align*} H_0 &= 1 \\ H_1 &= 2\xi \\ H_2 &= 4\xi^2 - 2 \\ H_3 &= 8\xi^3 - 12\xi \\ H_4 &= 16\xi^4 - 48\xi^2 + 12 \\ H_5 &= 32\xi^5 - 160\xi^3 + 120\xi \\ &\qquad\vdots \end{align*}\]定態 $\psi_n(x)$
調和振盪子的規範化定態如下:
\[\psi_n(x) = \left(\frac{m\omega}{\pi\hbar} \right)^{1/4} \frac{1}{\sqrt{2^n n!}}H_n(\xi)e^{-\xi^2/2}.\]這與調和振盪子的代數解法中得到的結果(式 [27])一致。
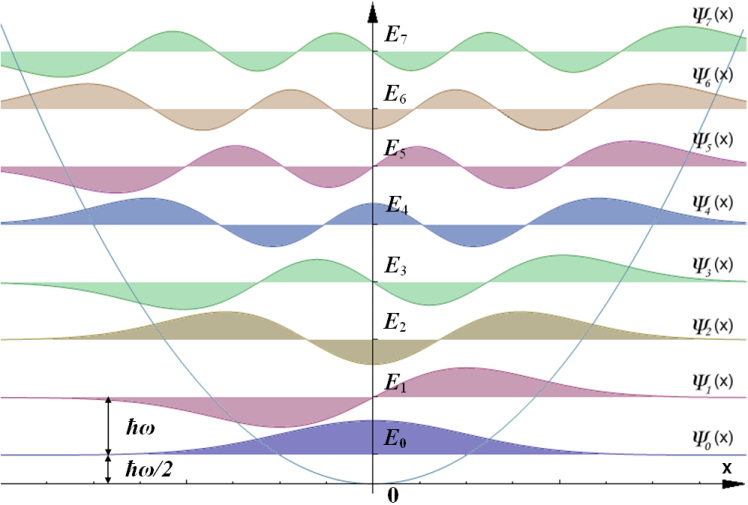
下圖顯示了前 8 個 $n$ 值對應的定態 $\psi_n(x)$ 和概率密度 $|\psi_n(x)|^2$。我們可以看到量子振盪子的本徵函數交替出現偶函數和奇函數。
圖片來源
- 作者:維基媒體用戶 AllenMcC
- 許可證:CC BY-SA 3.0
圖片來源
- 作者:維基媒體用戶 AllenMcC
- 許可證:Public Domain
量子振盪子與相應的經典振盪子有很大的不同,不僅能量是量子化的,位置 $x$ 的概率分布也顯示出奇特的特性。
- 在經典力學上不可能存在的區域(大於給定 $E$ 的經典振幅的 $x$)也有非零的概率被發現,雖然概率很低,但粒子可能存在
- 對於所有奇數 $n$ 的定態,在中心處發現粒子的概率為 $0$
隨著 $n$ 的增大,量子振盪子會越來越接近經典振盪子。下圖顯示了位置 $x$ 的經典概率分布(虛線)和 $n=30$ 時的量子態 $|\psi_{30}|^2$(實線)。如果我們平滑地連接凹凸不平的部分,兩個圖形大致吻合。
圖片來源
- 作者:維基媒體用戶 AkanoToE
- 許可證:Public Domain
量子振盪子概率分布的互動可視化
以下是我親自編寫的基於 Plotly.js 的響應式可視化。您可以通過滑塊調整 $n$ 值,查看位置 $x$ 的經典概率分布和 $|\psi_n|^2$ 的輪廓。
此外,如果您的電腦上可以使用 Python,並且安裝了 Numpy、Plotly 和 Dash 庫,您也可以運行同一倉庫中的 /src/quantum_oscillator.py Python 腳本來查看結果。