Teorema da Adição Harmônica

TL;DR

Teorema da Adição Harmônica

• \[a\sin \theta + b\cos \theta = \sqrt{a^{2}+b^{2}} \sin(\theta+\alpha)\]

\[(\text{onde}\ \cos \alpha = \frac{a}{\sqrt{a^{2}+b^{2}}},\ \sin \alpha = \frac{b}{\sqrt{a^{2}+b^{2}}})\]

• \[a\sin \theta + b\cos \theta = \sqrt{a^{2}+b^{2}} \cos(\theta-\beta)\]

\[(\text{onde}\ \cos \beta = \frac{b}{\sqrt{a^{2}+b^{2}}},\ \sin \beta = \frac{a}{\sqrt{a^{2}+b^{2}}})\]

Pré-requisitos

• Fórmulas de Adição Trigonométrica

Teorema da Adição Harmônica

Para uma função $f(\theta) = a \cos \theta + b \sin \theta$ que é uma soma de funções trigonométricas, sempre existem números reais $\alpha$ e $\beta$ que satisfazem $f(\theta)=\sqrt{a^2+b^2} \sin(\theta+\alpha) = \sqrt{a^2+b^2} \cos(\theta-\beta)$.

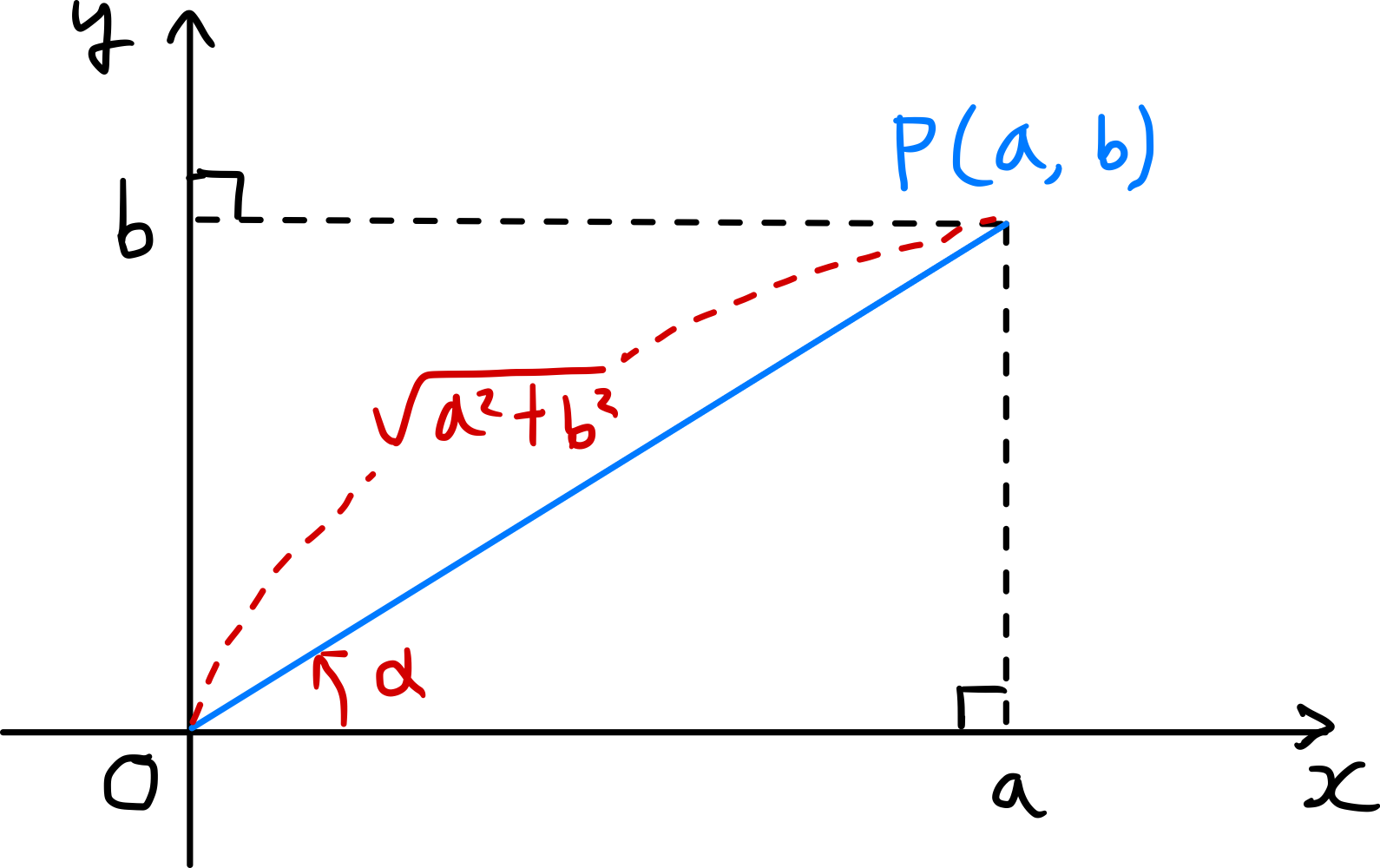
Como mostrado na figura, se marcarmos o ponto $P(a,b)$ no plano coordenado e chamarmos de $\alpha$ o ângulo formado entre o segmento $\overline{OP}$ e a direção positiva do eixo $x$, temos

\[\overline{OP} = \sqrt{a^2+b^2}\]

e

\[\cos \alpha = \frac{a}{\sqrt{a^{2} + b^{2}}},\ \sin \alpha = \frac{b}{\sqrt{a^{2} + b^{2}}} \tag{1}\]

Neste caso,

\[\begin{align*} a \sin \theta + b \cos \theta &= \sqrt{a^{2}+b^{2}} \left(\frac{a}{\sqrt{a^{2}+b^{2}}}\sin \theta + \frac{b}{\sqrt{a^{2}+b^{2}}}\cos \theta \right) \\ &= \sqrt{a^{2}+b^{2}}(\cos \alpha \sin \theta + \sin \alpha \cos \theta) \\ &= \sqrt{a^{2}+b^{2}} \sin(\theta + \alpha). \tag{2} \end{align*}\]

Da mesma forma, se marcarmos o ponto $P^{\prime}(b,a)$ e chamarmos de $\beta$ o ângulo formado entre o segmento $\overline{OP^{\prime}}$ e a direção positiva do eixo $x$, obtemos:

\[a \sin \theta + b \cos \theta = \sqrt{a^{2}+b^{2}}\cos(\theta-\beta). \tag{3}\] \[\text{onde}\ \cos \beta = \frac{b}{\sqrt{a^{2}+b^{2}}},\ \sin \beta = \frac{a}{\sqrt{a^{2}+b^{2}}}.\]

A transformação de uma função trigonométrica da forma $a \sin \theta + b \sin \theta$ em uma forma $r\sin(\theta+\alpha)$ ou $r\cos(\theta-\beta)$ é chamada de Adição Harmônica.

Exemplo

Seja a função $f(\theta)=-\sqrt{3}\sin \theta + \cos \left(\theta - \frac{\pi}{3} \right)$. Encontre os valores máximo e mínimo da função $f(\theta)$ no intervalo $[0, 2\pi]$.

1. Transformar para a forma $a\sin\theta + b\cos\theta$

Usando as Fórmulas de Adição Trigonométrica, podemos transformar a função dada:

\[\begin{align*} f(\theta) &= -\sqrt{3}\sin \theta + \cos \left(\theta - \frac{\pi}{3} \right) \\ &= -\sqrt{3}\sin \theta + \left( \cos\theta \cos\frac{\pi}{3} + \sin\theta \sin\frac{\pi}{3} \right) \\ &= -\frac{\sqrt{3}}{2}\sin\theta + \frac{1}{2}\cos\theta . \end{align*}\]

2. Transformar para a forma $r\sin(\theta+\alpha)$

Fazendo $a=-\frac{\sqrt{3}}{2}$ e $b=\frac{1}{2}$, temos:

\[r = \sqrt{a^2+b^2} = \sqrt{\frac{3}{4}+\frac{1}{4}} = 1\]

Além disso, existe um único valor real $\alpha$ tal que $0 \leq \alpha<2\pi$, $\cos\alpha = a$ e $\sin\alpha = b$. A partir dos valores trigonométricos para ângulos especiais, podemos determinar que $\alpha = \frac{5}{6}\pi$.

Portanto, transformando a função dada $f(\theta)$ para a forma $r\sin(\theta+\alpha)$, obtemos:

\[f(\theta) = \sin \left(\theta + \frac{5\pi}{6} \right).\]

3. Encontrar os valores máximo e mínimo no intervalo dado

A função $f(\theta) = \sin \left(\theta + \frac{5\pi}{6} \right)$ é uma função periódica com período $2\pi$, e no intervalo dado, ela tem um valor máximo de $1$ e um valor mínimo de $-1$.

\[\therefore M=1,\ m=-1\]