Transferência de energia por colisão

TL;DR

• A energia total e o momento são conservados durante a colisão
• Íons que perderam todos os elétrons e ficaram apenas com o núcleo atômico, e elétrons, possuem apenas energia cinética
• Átomos neutros e íons que perderam apenas alguns elétrons têm energia interna, e podem ocorrer excitação, desexcitação ou ionização dependendo da mudança na energia potencial
• Classificação dos tipos de colisão com base na mudança da energia cinética antes e depois da colisão:
  • Colisão elástica: A quantidade total de energia cinética permanece constante antes e depois da colisão
  • Colisão inelástica: Há perda de energia cinética durante o processo de colisão
    • Excitação
    • Ionização
  • Colisão superelástica: Há aumento de energia cinética durante o processo de colisão
    • Desexcitação
• Taxa de transferência de energia por colisão elástica:
  • Taxa de transferência de energia por colisão individual: $\zeta_L = \cfrac{4m_1m_2}{(m_1+m_2)^2}\cos^2\theta_2$
  • Taxa média de transferência de energia por colisão: $\overline{\zeta_L} = \cfrac{4m_1m_2}{(m_1+m_2)^2}\overline{\cos^2\theta_2} = \cfrac{2m_1m_2}{(m_1+m_2)^2}$
    • Quando $m_1 \approx m_2$: $\overline{\zeta_L} \approx \cfrac{1}{2}$, ocorre transferência eficaz de energia, atingindo rapidamente o equilíbrio térmico
    • Quando $m_1 \ll m_2$ ou $m_1 \gg m_2$: $\overline{\zeta_L} \approx 10^{-5}\sim 10^{-4}$, a eficiência da transferência de energia é muito baixa, tornando difícil atingir o equilíbrio térmico. Esta é a razão pela qual em plasmas fracamente ionizados, $T_e \gg T_i \approx T_n$, com a temperatura dos elétrons sendo muito diferente da temperatura dos íons e átomos neutros.
• Taxa de transferência de energia por colisão inelástica:
  • Taxa máxima de conversão de energia interna por colisão única: $\zeta_L = \cfrac{\Delta U_\text{max}}{\cfrac{1}{2}m_1v_1^2} = \cfrac{m_2}{m_1+m_2}\cos^2\theta_2$
  • Taxa média máxima de conversão de energia interna: $\overline{\zeta_L} = \cfrac{m_2}{m_1+m_2}\overline{\cos^2\theta_2} = \cfrac{m_2}{2(m_1+m_2)}$
    • Quando $m_1 \approx m_2$: $\overline{\zeta_L} \approx \cfrac{1}{4}$
    • Quando $m_1 \gg m_2$: $\overline{\zeta_L} \approx 10^{-5}\sim 10^{-4}$
    • Quando $m_1 \ll m_2$: $\overline{\zeta_L} = \cfrac{1}{2}$, sendo a forma mais eficiente de aumentar a energia interna do alvo da colisão (íon ou átomo neutro) e levá-lo a um estado excitado. Esta é a razão pela qual a ionização por elétrons (geração de plasma), excitação (emissão de luz) e dissociação de moléculas (geração de radicais) ocorrem facilmente.

Pré-requisitos

• Partículas subatômicas e componentes do átomo

Colisões entre partículas no plasma

• A energia total e o momento são conservados durante a colisão
• Íons que perderam todos os elétrons e ficaram apenas com o núcleo atômico, e elétrons, possuem apenas energia cinética
• Átomos neutros e íons que perderam apenas alguns elétrons têm energia interna, e podem ocorrer excitação, desexcitação ou ionização dependendo da mudança na energia potencial
• Classificação dos tipos de colisão com base na mudança da energia cinética antes e depois da colisão:
  • Colisão elástica: A quantidade total de energia cinética permanece constante antes e depois da colisão
  • Colisão inelástica: Há perda de energia cinética durante o processo de colisão
    • Excitação
    • Ionização
  • Colisão superelástica: Há aumento de energia cinética durante o processo de colisão
    • Desexcitação

Transferência de energia por colisão elástica

Taxa de transferência de energia por colisão individual

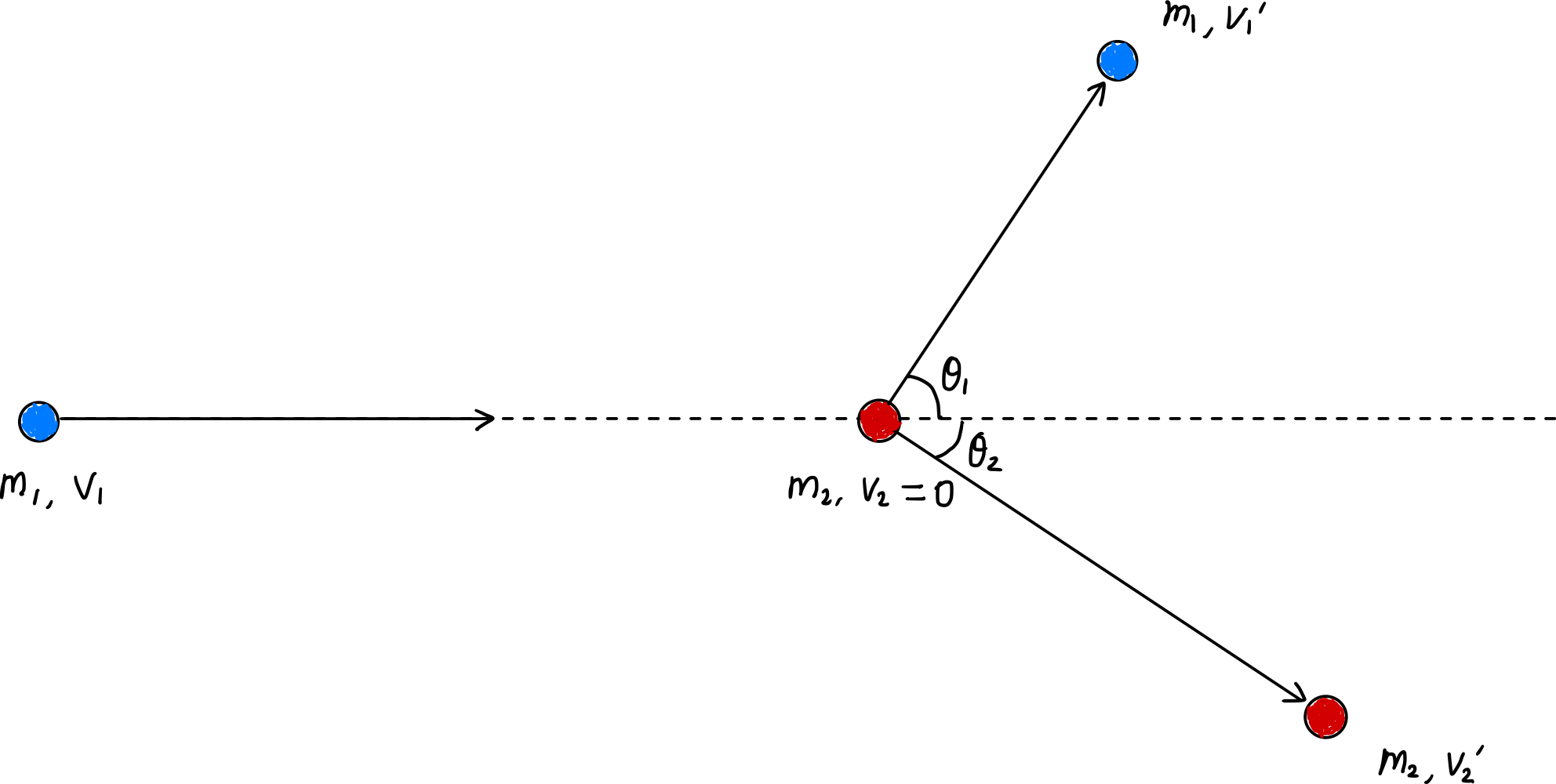
Em uma colisão elástica, o momento e a energia cinética são conservados antes e depois da colisão.

Estabelecendo as equações de conservação do momento para os eixos $x$ e $y$, temos:

\[\begin{gather*} m_1v_1 = m_1v_1^{\prime}\cos\theta_1 + m_2v_2^{\prime}\cos\theta_2, \label{eqn:momentum_conservation_x}\tag{1} \\ m_1v_1^{\prime}\sin\theta_1 = m_2v_2^{\prime}\sin\theta_2 \label{eqn:momentum_conservation_y}\tag{2} \end{gather*}\]

Além disso, pela conservação de energia:

\[\frac{1}{2}m_1v_1^2 = \frac{1}{2}m_1{v_1^{\prime}}^2 + \frac{1}{2}m_2{v_2^{\prime}}^2\] \[v_1^2 = {v_1^{\prime}}^2 + \frac{m_2}{m_1}{v_2^{\prime}}^2 \label{eqn:energy_conservation}\tag{3}\]

Da equação ($\ref{eqn:momentum_conservation_x}$):

\[m_1 v_1^{\prime} \cos \theta_1 = m_1v_1 - m_2v_2^{\prime} \cos \theta_2 \label{eqn:momentum_conservation_x_2}\tag{4}\]

Elevando ao quadrado e somando as equações ($\ref{eqn:momentum_conservation_y}$) e ($\ref{eqn:momentum_conservation_x_2}$):

\[\begin{align*} (m_1v_1^{\prime})^2 &= (m_2 v_2^\prime \sin \theta_2)^2 + (m_1 v_1 - m_2 v_2^\prime \cos \theta_2)^2 \\ &= m_1^2 v_1^2 - 2 m_1 m_2 v_1 v_2^\prime \cos \theta_2 + m_2^2 {v_2^\prime}^2 \tag{5} \end{align*}\]

Dividindo ambos os lados por $m_1^2$:

\[{v_1^{\prime}}^2 = v_1^2 - 2 \frac{m_2}{m_1} v_1 v_2^\prime \cos \theta_2 + \left(\frac{m_2}{m_1}\right)^2 {v_2^\prime}^2 \label{eqn:momentum_conservation}\tag{6}\]

Substituindo a equação ($\ref{eqn:energy_conservation}$) nesta, podemos reorganizar como:

\[\begin{gather*} \left( \frac{m_2}{m_1} \right) {v_2^\prime}^2 = 2 \left( \frac{m_2}{m_1} \right) v_1 v_2^\prime \cos \theta_2 - \left( \frac{m_2}{m_1} \right)^2 {v_2^\prime}^2 \\ 2v_1 \cos \theta_2 = \left(\frac{m_1 + m_2}{m_1} \right) v_2^\prime \\ v_2^{\prime} = \frac{2m_1v_1\cos\theta_2}{m_1 + m_2}. \label{eqn:v_2_prime}\tag{7} \end{gather*}\]

A partir disso, obtemos a taxa de transferência de energia $\zeta_L$ da seguinte forma:

\[\begin{align*} \therefore \zeta_L &= \frac{\cfrac{1}{2}m_2{v_2^\prime}^2}{\cfrac{1}{2}m_1v_1^2} = \frac{m_2}{m_1v_1^2} {\left(\frac{2m_1v_1\cos\theta_2}{m_1 + m_2} \right)}^2 \\ &= \frac{4m_1m_2}{(m_1+m_2)^2}\cos^2\theta_2. \quad \blacksquare \label{eqn:elastic_E_transfer_rate}\tag{8} \end{align*}\]

Taxa média de transferência de energia por colisão

Para ângulos de 0 a 2π, $\sin^2{\theta_2}+\cos^2{\theta_2}=1$ e $\overline{\sin^2{\theta_2}}=\overline{\cos^2{\theta_2}}$, portanto:

\[\begin{align*} \overline{\cos^2{\theta_2}} &= \overline{(1-\sin^2{\theta_2})} = 1 - \overline{\sin^2{\theta_2}} \\ &= 1 - \overline{\cos^2{\theta_2}} \end{align*}\] \[\begin{gather*} 2 \cdot \overline{\cos^2{\theta_2}} = 1 \\ \overline{\cos^2{\theta_2}} = \frac{1}{2}. \end{gather*}\]

Substituindo isso na equação ($\ref{eqn:elastic_E_transfer_rate}$) que encontramos anteriormente:

\[\overline{\zeta_L} = \frac{4m_1m_2}{(m_1+m_2)^2}\overline{\cos^2\theta_2} = \frac{2m_1m_2}{(m_1+m_2)^2}. \quad \blacksquare \label{eqn:elastic_E_mean_transfer_rate}\tag{9}\]

Quando $m_1 \approx m_2$

Isso se aplica a colisões elétron-elétron, íon-íon, átomo neutro-átomo neutro, íon-átomo neutro. Nestes casos:

\[\overline{\zeta_L} = \frac{2m_1m_2}{(m_1+m_2)^2} \approx \frac{1}{2} \label{eqn:elastic_similar_m}\tag{10}\]

Ocorre uma transferência eficaz de energia, atingindo rapidamente o equilíbrio térmico.

Quando $m_1 \ll m_2$ ou $m_1 \gg m_2$

Isso se aplica a colisões elétron-íon, elétron-átomo neutro, íon-elétron, átomo neutro-elétron. Nestes casos:

\[\overline{\zeta_L} = \frac{2m_1m_2}{(m_1+m_2)^2} \approx \frac{2m_1}{m_2}\text{ (baseado em }m_1 \ll m_2 \text{)} \approx 10^{-5}\sim 10^{-4} \label{eqn:elastic_different_m}\tag{11}\]

A eficiência da transferência de energia é muito baixa, tornando difícil atingir o equilíbrio térmico. Esta é a razão pela qual em plasmas fracamente ionizados, $T_e \gg T_i \approx T_n$, com a temperatura dos elétrons sendo muito diferente da temperatura dos íons e átomos neutros.

Transferência de energia por colisão inelástica

Taxa máxima de conversão de energia interna por colisão única

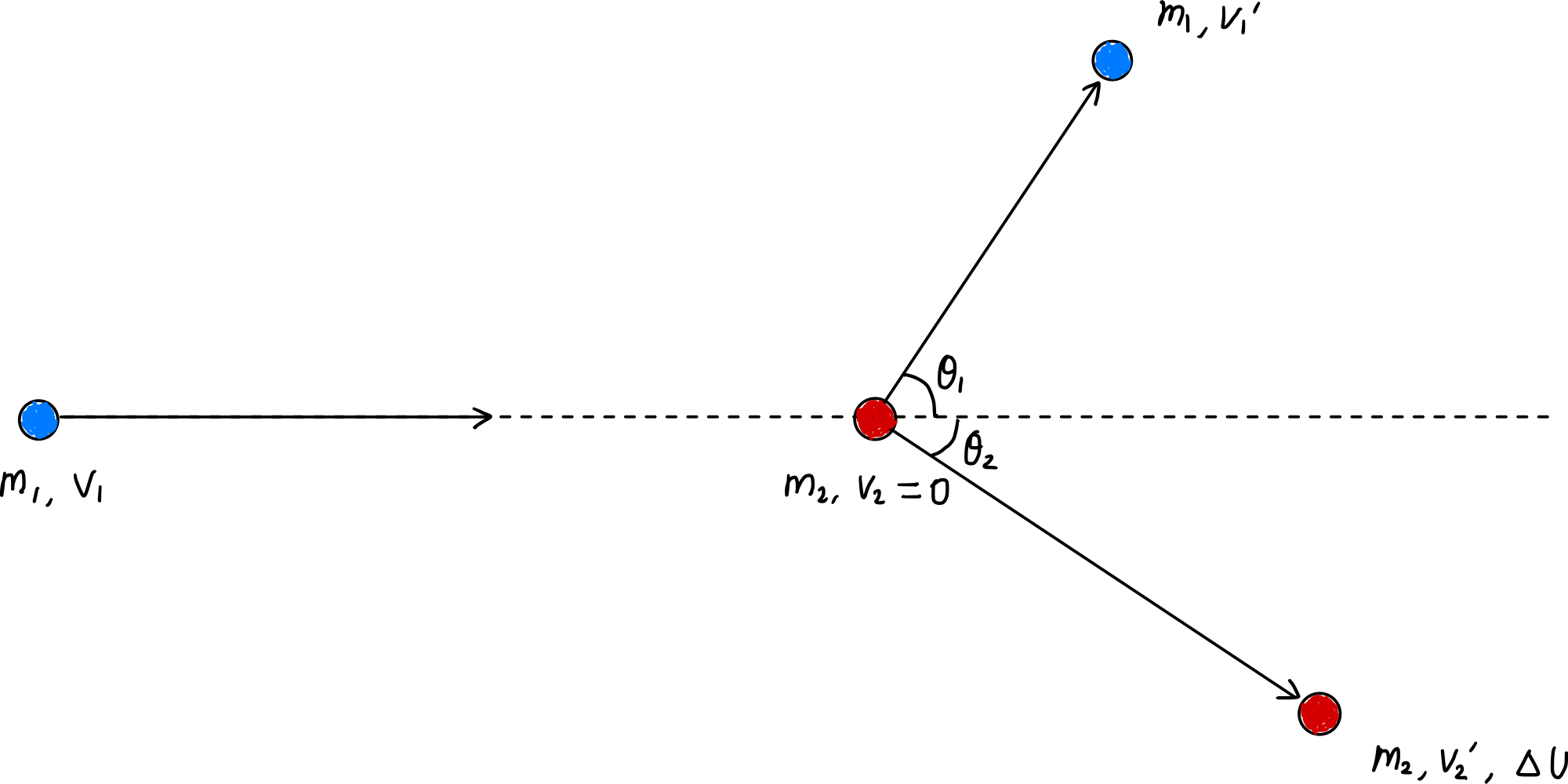
A conservação do momento (equação [$\ref{eqn:momentum_conservation}$]) também se aplica neste caso, mas como é uma colisão inelástica, a energia cinética não é conservada. Neste caso, a energia cinética perdida pela colisão inelástica é convertida em energia interna $\Delta U$, então:

\[\Delta U = \frac{1}{2} m_1 v_1^2 - \left( \frac{1}{2} m_1 {v_1^{\prime}}^2 + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right) \label{eqn:delta_U}\tag{12}\]

Agora, substituindo a equação ($\ref{eqn:momentum_conservation}$) aqui e reorganizando, obtemos:

\(\begin{align*} \Delta U &= \frac{1}{2} m_1 v_1^2 - \left[ \frac{1}{2} m_1 \left( v_1^2 - 2 \frac{m_2}{m_1} v_1 v_2^{\prime} \cos \theta_2 + \left( \frac{m_2}{m_1} v_2^{\prime} \right)^2 \right) + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right] \\ &= \frac{1}{2} m_1 v_1^2 - \left[ \frac{1}{2} m_1 v_1^2 - m_2 v_1 v_2^{\prime} \cos \theta_2 + \frac{1}{2} \frac{m_2^2}{m_1} {v_2^{\prime}}^2 + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right] \\ &= m_2 v_1 v_2^{\prime} \cos \theta_2 - \frac{1}{2}m_2{v_2^{\prime}}^2\left(\frac{m_1 + m_2}{m_1}\right) \label{eqn:delta_U_2}\tag{13} \end{align*}\).

Diferenciando $\Delta U$ em relação a $v_2^\prime$, encontrando o ponto extremo onde o valor dessa derivada é 0 e o valor máximo nesse ponto:

\[\cfrac{d \Delta U}{d v_2^{\prime}} = m_2 v_1 \cos \theta_2 - m_2 v_2^{\prime} \left( \frac{m_1 + m_2}{m_1} \right) = 0 \tag{14}\] \[\begin{gather*} v_2^{\prime} \left( \frac{m_1 + m_2}{m_1} \right) = v_1 \cos \theta_2 \\ v_2^\prime = \frac{m_1v_1\cos\theta_2}{m_1+m_2}. \end{gather*}\] \[\therefore v_2^{\prime} = \frac{m_1v_1\cos\theta_2}{m_1+m_2} \text{ quando } \Delta U_\text{max} = \frac{1}{2}\frac{m_1m_2 v_1^2 \cos^2\theta_2}{m_1 + m_2}. \label{eqn:delta_U_max}\tag{15}\]

A partir disso, a taxa máxima de conversão $\zeta_L$ de energia cinética em energia interna possível por uma única colisão inelástica é:

\[\zeta_L = \frac{\Delta U_\text{max}}{\cfrac{1}{2}m_1v_1^2} = \frac{m_2}{m_1+m_2}\cos^2\theta_2. \quad \blacksquare \label{eqn:inelastic_E_transfer_rate}\tag{16}\]

Taxa média máxima de conversão de energia interna

Da mesma forma, substituindo $\overline{\cos^2{\theta_2}} = \cfrac{1}{2}$ na equação ($\ref{eqn:inelastic_E_transfer_rate}$), obtemos:

\[\overline{\zeta_L} = \frac{m_2}{m_1+m_2}\overline{\cos^2\theta_2} = \frac{m_2}{2(m_1+m_2)}. \label{eqn:inelastic_E_mean_transfer_rate}\tag{17}\]

Quando $m_1 \approx m_2$

Isso se aplica a colisões íon-íon, íon-átomo neutro, átomo neutro-átomo neutro.

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} = \frac{1}{4}. \label{eqn:inelastic_similar_m}\tag{18}\]

Quando $m_1 \gg m_2$

Isso se aplica a colisões íon-elétron, átomo neutro-elétron.

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} \approx \frac{m_2}{2m_1} \approx 10^{-5}\sim 10^{-4}. \label{eqn:inelastic_ion_electron}\tag{19}\]

Quando $m_1 \ll m_2$

Isso se aplica a colisões elétron-íon, elétron-átomo neutro. Enquanto os dois casos anteriores não eram muito diferentes das colisões elásticas, este terceiro caso mostra uma diferença importante. Neste caso:

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} \approx \frac{m_2}{2m_2} = \frac{1}{2} \label{eqn:inelastic_electron_ion}\tag{20}\]

Esta é a forma mais eficiente de aumentar a energia interna do alvo da colisão (íon ou átomo neutro) e levá-lo a um estado excitado. Isso será discutido mais adiante, mas é a razão pela qual a ionização por elétrons (geração de plasma), excitação (emissão de luz) e dissociação de moléculas (geração de radicais) ocorrem facilmente.