Definição de plasma, conceito de temperatura e a equação de Saha

TL;DR

• Plasma: Gás quase neutro composto de partículas carregadas e neutras que exibe comportamento coletivo
• ‘Comportamento coletivo’ do plasma:
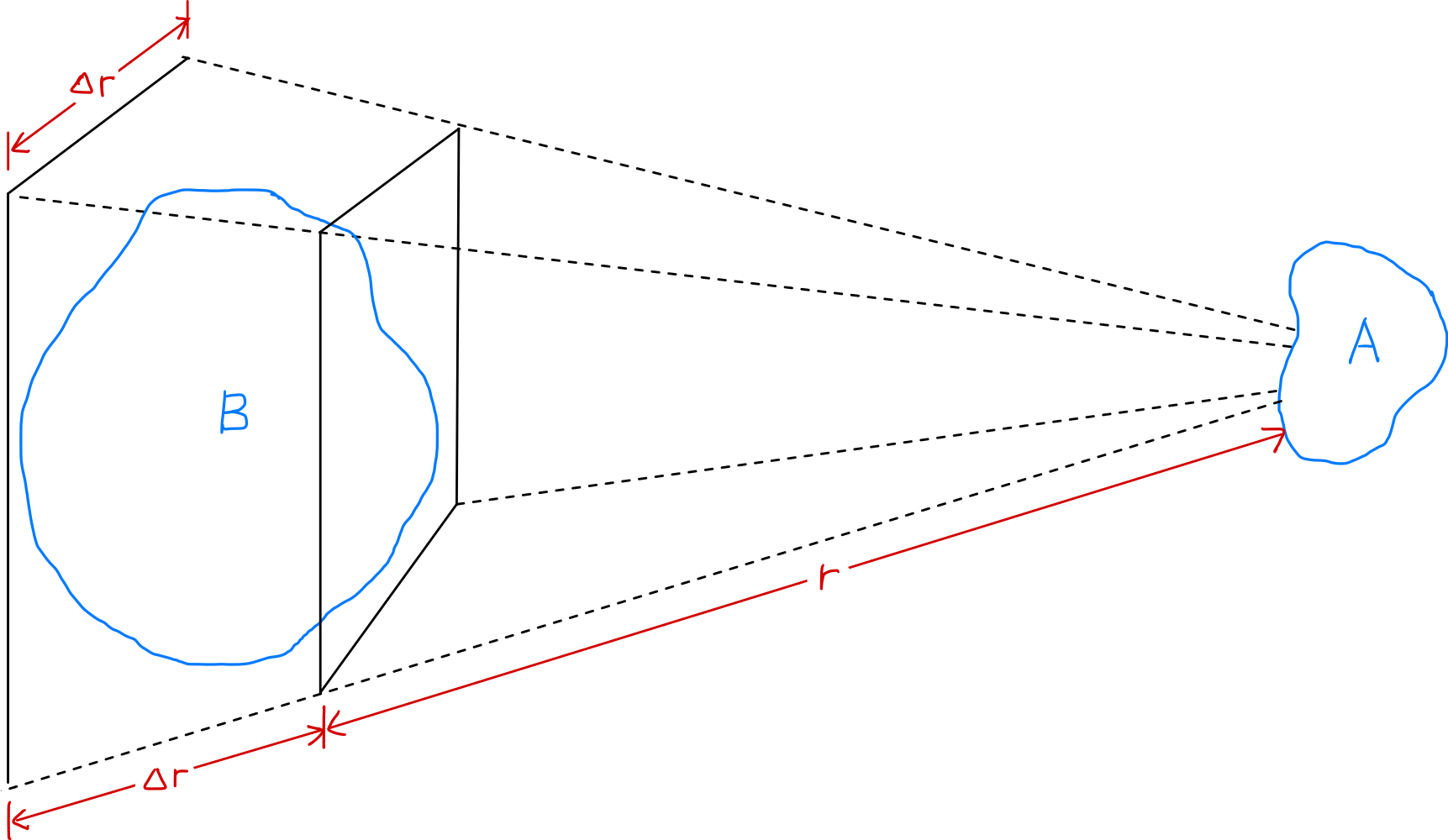
  • A força elétrica entre duas regiões A e B no plasma diminui com $1/r^2$ à medida que a distância aumenta
  • No entanto, quando o ângulo sólido ($\Delta r/r$) é constante, o volume da região B do plasma que pode influenciar A aumenta com $r^3$
  • Portanto, as partes constituintes do plasma podem exercer forças significativas umas sobre as outras mesmo a longas distâncias
• Equação de Saha: Relação entre o estado de ionização, temperatura e pressão de um gás em equilíbrio térmico

\[\frac{n_{i+1}n_e}{n_i} = \frac{2}{\lambda_{\text{th}}^3}\frac{g_{i+1}}{g_i}\exp{\left[-\frac{\epsilon_{i+1}-\epsilon_i}{k_B T}\right]}\]

• Conceito de temperatura na física de plasmas:
  • A energia cinética média por partícula em gases e plasmas está intimamente relacionada à temperatura, e essas duas quantidades são intercambiáveis
  • Na física de plasmas, é convencional expressar a temperatura em unidades de energia $\mathrm{eV}$ como o valor de $kT$
    • $1\mathrm{eV}=11600\mathrm{K}$
  • Plasmas podem ter várias temperaturas diferentes simultaneamente, e em particular, a temperatura dos elétrons ($T_e$) e a temperatura dos íons ($T_i$) podem ser significativamente diferentes em alguns casos
• Plasma de baixa temperatura vs. plasma de alta temperatura:
  • Temperatura do plasma:
    • Plasma de baixa temperatura: $T_e \text{(>10.000℃)} \gg T_i \approx T_g \text{(}\sim\text{100℃)}$ $\rightarrow$ Plasma não-equilibrado (non-equilibrium plasma)
    • Plasma de alta temperatura (térmico): $T_e \approx T_i \approx T_g \text{(>10.000℃)}$ $\rightarrow$ Plasma em equilíbrio (equilibrium plasma)
  • Densidade do plasma:
    • Plasma de baixa temperatura: $n_g \gg n_i \approx n_e$ $\rightarrow$ Baixa taxa de ionização, maioria das partículas são neutras
    • Plasma de alta temperatura (térmico): $n_g \approx n_i \approx n_e $ $\rightarrow$ Alta taxa de ionização
  • Capacidade térmica do plasma:
    • Plasma de baixa temperatura: Temperatura dos elétrons é alta, mas a densidade é baixa, e a maioria são partículas neutras a temperaturas relativamente baixas, então a capacidade térmica é pequena e não é quente
    • Plasma de alta temperatura (térmico): Elétrons, íons e partículas neutras estão todos a altas temperaturas, então a capacidade térmica é grande e é quente

Pré-requisitos

• Partículas subatômicas e componentes do átomo
• Distribuição de Maxwell-Boltzmann (mecânica estatística)
• Massa e energia, partículas e ondas
• Simetria e leis de conservação (mecânica quântica), degenerescência

Definição de plasma

Normalmente, em textos que explicam o plasma para não especialistas, o plasma é definido da seguinte forma:

O quarto estado da matéria, após sólido, líquido e gasoso, obtido aquecendo um gás até um estado de temperatura ultra-alta onde os átomos constituintes são separados em elétrons e íons positivos até se ionizarem

Isso não está errado, e até mesmo o site do Instituto de Energia de Fusão da Coreia (Korea Institute of Fusion Energy) o apresenta dessa forma. É também uma definição popular que se pode encontrar facilmente ao pesquisar sobre plasma.

No entanto, embora essa expressão esteja correta, não pode ser considerada uma definição rigorosa. Mesmo os gases em nosso ambiente à temperatura e pressão ambiente estão ligeiramente ionizados, embora em uma proporção extremamente pequena, mas não chamamos isso de plasma. Quando dissolvemos uma substância de ligação iônica como o cloreto de sódio em água, ela se separa em íons carregados, mas essa solução também não é um plasma.
Ou seja, embora o plasma seja um estado ionizado da matéria, nem tudo que está ionizado pode ser chamado de plasma.

De forma mais rigorosa, o plasma pode ser definido da seguinte maneira:

Um plasma é um gás quase neutro de partículas carregadas e neutras que exibe comportamento coletivo.

por Francis F. Chen

O que significa ‘quase neutralidade (quasineutrality)’ será discutido posteriormente ao abordar o blindagem de Debye (Debye shielding). Aqui, vamos examinar o que significa o ‘comportamento coletivo (collective behavior)’ do plasma.

Comportamento coletivo do plasma

No caso de um gás não ionizado composto de partículas neutras, cada molécula de gás é eletricamente neutra, portanto a força eletromagnética líquida atuante é $0$, e a influência da gravidade também pode ser ignorada. As moléculas se movem sem interferência até colidirem com outras moléculas, e as colisões entre moléculas determinam o movimento das partículas. Mesmo que algumas partículas sejam ionizadas e carregadas, como a proporção de partículas ionizadas no gás total é muito baixa, a influência elétrica dessas partículas carregadas diminui com $1/r^2$ com a distância e não alcança longas distâncias.

No entanto, em um plasma que contém muitas partículas carregadas, a situação é completamente diferente. O movimento das partículas carregadas pode causar concentrações locais de cargas positivas ou negativas, criando campos elétricos. Além disso, o movimento de cargas cria correntes, e as correntes criam campos magnéticos. Esses campos elétricos e magnéticos podem influenciar outras partículas distantes, mesmo sem colisões entre partículas.

Vamos examinar como a intensidade da força elétrica entre duas regiões de plasma ligeiramente carregadas $A$ e $B$ varia com a distância $r$. A força elétrica (força de Coulomb) entre $A$ e $B$ diminui com $1/r^2$ à medida que a distância aumenta. No entanto, quando o ângulo sólido ($\Delta r/r$) é constante, o volume da região de plasma $B$ que pode influenciar $A$ aumenta com $r^3$. Portanto, as partes constituintes do plasma podem exercer forças significativas umas sobre as outras mesmo a longas distâncias. Essas forças elétricas de longo alcance permitem que o plasma exiba uma ampla variedade de padrões de movimento, e são a razão pela qual existe um campo de estudo independente chamado física de plasmas. O ‘comportamento coletivo (collective behavior)’ significa que o movimento de uma região é influenciado não apenas pelas condições locais nessa região, mas também pelo estado do plasma em regiões distantes.

Equação de Saha (Saha equation)

A equação de Saha (Saha equation) é uma relação entre o estado de ionização, temperatura e pressão de um gás em equilíbrio térmico, concebida pelo astrofísico indiano Meghnad Saha.

\[\frac{n_{i+1}n_e}{n_i} = \frac{2}{\lambda_{\text{th}}^3}\frac{g_{i+1}}{g_i}\exp{\left[-\frac{\epsilon_{i+1}-\epsilon_i}{k_B T}\right]} \label{eqn:saha_eqn}\tag{1}\]

• $n_i$: densidade de íons positivos $i$ (íons positivos que perderam $i$ elétrons)
• $g_i$: degenerescência do estado do íon positivo $i$
• $\epsilon_i$: energia necessária para remover $i$ elétrons de um átomo neutro para criar um íon positivo $i$
  • $\epsilon_{i+1}-\epsilon_i$: energia de ionização de $(i+1)$-ésima ordem
• $n_e$: densidade de elétrons
• $k_B$: constante de Boltzmann
• $\lambda_{\text{th}}$: comprimento de onda térmico de de Broglie (comprimento de onda médio de de Broglie dos elétrons no gás a uma dada temperatura)

\[\lambda_{\text{th}} \equiv \frac{h}{\sqrt{2\pi m_e k_B T}} \quad \text{ (}h\text{: constante de Planck)} \label{eqn:lambda_th}\tag{2}\]

• $m_e$: massa do elétron
• $T$: temperatura do gás

Se apenas um nível de ionização for importante e a produção de íons positivos de carga 2 ou superior puder ser ignorada, podemos simplificar colocando $n_1=n_i=n_e$, $n_0=n_n$, $U_i = \epsilon = \epsilon_1$, $i=0$ da seguinte forma:

\[\begin{align*} \frac{n_i^2}{n_n} &= \frac{2}{\lambda_{th}^3}\frac{g_1}{g_0}\exp{\left[-\frac{\epsilon}{k_B T} \right]} \label{eqn:saha_eqn_approx}\tag{3}\\ &= 2\left(\frac{2\pi m_e k_B T}{h^2}\right)^{3/2}\frac{g_1}{g_0}e^{-U_i/{k_B T}} \\ &= 2\frac{g_1}{g_0}\left(\frac{2\pi m_e k_B}{h^2}\right)^{3/2}T^{3/2}e^{-U_i/{k_B T}}. \label{eqn:saha_eqn_approx_2}\tag{4} \end{align*}\]

Taxa de ionização do ar (nitrogênio) em condições de temperatura e pressão ambiente

Na equação acima, o valor de $2 \cfrac{g_1}{g_0}$ varia para cada componente do gás, mas em muitos casos, a ordem de grandeza deste valor é $1$. Portanto, podemos aproximar grosseiramente da seguinte forma:

\[\frac{n_i^2}{n_n} \approx \left(\frac{2\pi m_e k_B}{h^2}\right)^{3/2} T^{3/2} e^{-U_i/{k_B T}}.\]

No sistema SI, os valores das constantes fundamentais $m_e$, $k_B$, $h$ são respectivamente:

• $m_e \approx 9,11 \times 10^{-31} \mathrm{kg}$
• $k_B \approx 1,38 \times 10^{-23} \mathrm{J/K}$
• $h \approx 6,63 \times 10^{-34} \mathrm{J \cdot s}$

Substituindo estes na equação acima, obtemos:

\[\frac{n_i^2}{n_n} \approx 2,4 \times 10^{21}\ T^{3/2} e^{-U_i/{k_B T}}. \label{eqn:fractional_ionization}\tag{5}\]

A partir disso, calculando o valor aproximado da taxa de ionização $n_i/(n_n + n_i) \approx n_i/n_n$ para o nitrogênio ($U_i \approx 14,5\mathrm{eV} \approx 2,32 \times 10^{-18}\mathrm{J}$) em condições de temperatura e pressão ambiente ($n_n \approx 3 \times 10^{25} \mathrm{m^{-3}}$, $T\approx 300\mathrm{K}$), obtemos:

\[\frac{n_i}{n_n} \approx 10^{-122}\]

o que é uma proporção extremamente baixa. Esta é a razão pela qual, diferentemente do ambiente espacial, quase não encontramos plasma naturalmente na atmosfera próxima à superfície terrestre e ao nível do mar.

Conceito de temperatura na física de plasmas

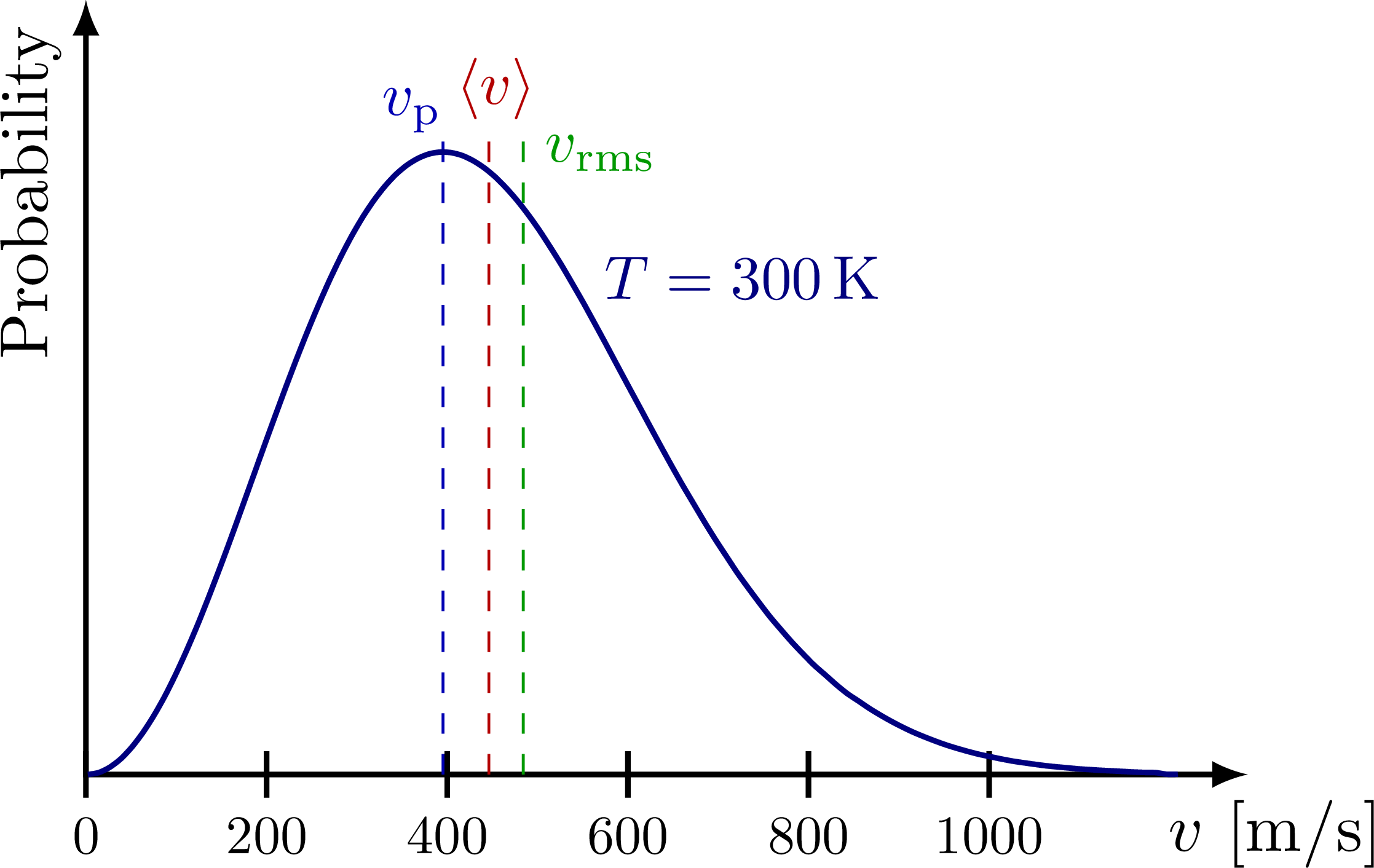
A velocidade das partículas que compõem um gás em equilíbrio térmico geralmente segue a distribuição de Maxwell-Boltzmann:

\[f(v) = \left(\frac{m}{2\pi k_B T} \right)^{3/2} 4\pi v^2 \exp{\left(-\frac{mv^2}{2k_B T} \right)} \label{eqn:maxwell_boltzmann_dist}\tag{6}\]

Fonte da imagem

• Autor: Autor do TikZ.net Izaak Neutelings
• Licença: CC BY-SA 4.0

• Velocidade mais provável (most probable speed): $v_p = \sqrt{\cfrac{2k_B T}{m}}$
• Velocidade média (mean speed): $\langle v \rangle = \sqrt{\cfrac{8k_B T}{\pi m}}$
• Velocidade quadrática média (RMS speed): $v_{rms} = \sqrt{\langle v^2 \rangle} = \sqrt{\cfrac{3k_B T}{m}}$

A energia cinética média por partícula a uma temperatura $T$ é $\cfrac{1}{2}m\langle v^2 \rangle = \cfrac{1}{2}mv_{rms}^2 = \cfrac{3}{2}k_B T$ (baseado em 3 graus de liberdade), determinada apenas pela temperatura. Como a energia cinética média por partícula em gases e plasmas está intimamente relacionada à temperatura, e essas duas quantidades são intercambiáveis, é convencional na física de plasmas expressar a temperatura em unidades de energia $\mathrm{eV}$. Para evitar confusão com as dimensões, a temperatura é expressa como o valor de $kT$ em vez da energia cinética média $\langle E_k \rangle$.

A temperatura $T$ quando $kT=1\mathrm{eV}$ é:

\[\begin{align*} T\mathrm{[K]} &= \frac{1,6 \times 10^{-19}\mathrm{[J]}}{1,38 \times 10^{-23}\mathrm{[J/K]}} \\ &= 11600\mathrm{[K]} \end{align*} \label{eqn:temp_conv_factor}\tag{7}\]

Portanto, na física de plasmas, quando a temperatura é expressa, $1\mathrm{eV}=11600\mathrm{K}$.
Ex: Para um plasma com temperatura de $2\mathrm{eV}$, o valor de $kT$ é $2\mathrm{eV}$, e a energia cinética média por partícula é $\cfrac{3}{2}kT=3\mathrm{eV}$.

Além disso, os plasmas podem ter várias temperaturas simultaneamente. Em plasmas, a frequência de colisões entre íons ou entre elétrons é maior do que a frequência de colisões entre elétrons e íons, e por isso, elétrons e íons podem atingir o equilíbrio térmico em temperaturas diferentes (temperatura dos elétrons $T_e$ e temperatura dos íons $T_i$), formando distribuições de Maxwell-Boltzmann separadas, e em alguns casos, a temperatura dos elétrons e a temperatura dos íons podem ser significativamente diferentes. Além disso, quando um campo magnético externo $\vec{B}$ é aplicado, mesmo para o mesmo tipo de partícula (por exemplo, íons), a intensidade da força de Lorentz recebida pode ser diferente dependendo se o movimento é paralelo ou perpendicular ao campo magnético, resultando em temperaturas diferentes $T_\perp$ e $T_\parallel$.

Relação entre temperatura, pressão e densidade

De acordo com a lei dos gases ideais:

\[PV = \left(\frac{N}{N_A}\right)RT = NkT \label{eqn:ideal_gas_law}\tag{8}\]

A partir disso, temos:

\[\begin{gather*} P = \frac{NkT}{V} = nkT, \\ n = \frac{P}{kT} \end{gather*} \label{eqn:relation_between_T_P_n}\tag{9}\]

Ou seja, a densidade do plasma é inversamente proporcional à temperatura ($kT$) e diretamente proporcional à pressão ($P$).

Classificação de plasmas: Plasma de baixa temperatura vs. Plasma de alta temperatura

Plasma frio de baixa temperatura não térmico	Plasma frio de baixa temperatura térmico	Plasma quente de alta temperatura
$T_i \approx T \approx 300 \mathrm{K}$ $T_i \ll T_e \leqslant 10^5 \mathrm{K}$	$T_i \approx T_e \approx T < 2 \times 10^4 \mathrm{K}$	$T_i \approx T_e > 10^6 \mathrm{K}$
Baixa pressão($\sim 100\mathrm{Pa}$) descarga luminescente e arco	Arcos a $100\mathrm{kPa}$ ($1\mathrm{atm}$)	Plasma cinético, plasma de fusão

Temperatura do plasma

Quando a temperatura dos elétrons é $T_e$, a temperatura dos íons é $T_i$, e a temperatura das partículas neutras é $T_g$:

• Plasma de baixa temperatura: $T_e \mathrm{(>10.000 K)} \gg T_i \approx T_g \mathrm{(\sim 100 K)}$ $\rightarrow$ Plasma não-equilibrado (non-equilibrium plasma)
• Plasma de alta temperatura (térmico): $T_e \approx T_i \approx T_g \mathrm{(>10.000 K)}$ $\rightarrow$ Plasma em equilíbrio (equilibrium plasma)

Densidade do plasma

Quando a densidade de elétrons é $n_e$, a densidade de íons é $n_i$, e a densidade de partículas neutras é $n_g$:

• Plasma de baixa temperatura: $n_g \gg n_i \approx n_e$ $\rightarrow$ Baixa taxa de ionização, maioria das partículas são neutras
• Plasma de alta temperatura (térmico): $n_g \approx n_i \approx n_e $ $\rightarrow$ Alta taxa de ionização

Capacidade térmica do plasma (Quão quente é?)

• Plasma de baixa temperatura: A temperatura dos elétrons é alta, mas a densidade é baixa, e a maioria são partículas neutras a temperaturas relativamente baixas, então a capacidade térmica é pequena e não é quente
• Plasma de alta temperatura (térmico): Elétrons, íons e partículas neutras estão todos a altas temperaturas, então a capacidade térmica é grande e é quente