Solução analítica do oscilador harmônico (The Harmonic Oscillator)

TL;DR

• Qualquer oscilação pode ser aproximada como uma oscilação harmônica simples (simple harmonic oscillation) se a amplitude for suficientemente pequena, o que torna a oscilação harmônica simples significativa na física
• Oscilador harmônico: $V(x) = \cfrac{1}{2}kx^2 = \cfrac{1}{2}m\omega^2 x^2$
• Introdução da variável adimensional $\xi$ e energia $K$ expressa em unidades de $\cfrac{1}{2}\hbar\omega$:
  • $\xi \equiv \sqrt{\cfrac{m\omega}{\hbar}}x$
  • $K \equiv \cfrac{2E}{\hbar\omega}$
  • $ \cfrac{d^2\psi}{d\xi^2} = \left(\xi^2-K \right)\psi $
• Quando $|\xi|^2 \to \infty$, a solução assintótica fisicamente permitida é $\psi(\xi) \to Ae^{-\xi^2/2}$, portanto,

\[\begin{gather*} \psi(\xi) = h(\xi)e^{-\xi^2/2} \quad \text{(onde }\lim_{\xi\to\infty}h(\xi)=A\text{)}, \\ \frac{d^2h}{d\xi^2}-2\xi\frac{dh}{d\xi}+(K-1)h = 0 \end{gather*}\]

• Expressando a solução desta equação na forma de série $ h(\xi) = a_0 + a_1\xi + a_2\xi^2 + \cdots = \sum_{j=0}^{\infty}a_j\xi^j$,

\[a_{j+2} = \frac{(2j+1-K)}{(j+1)(j+2)}a_j\]

• Para que esta solução seja normalizável, a série $\sum a_j$ deve ser finita, ou seja, deve existir um valor ‘máximo’ de $j$, $n\in \mathbb{N}$, tal que $a_j=0$ para $j>n$, portanto
  • $ K = 2n + 1 $
  • $ E_n = \left(n+\cfrac{1}{2} \right)\hbar\omega, \quad n=0,1,2,\dots $
• Geralmente, $h_n(\xi)$ é um polinômio de grau $n$ em $\xi$, e o restante, excluindo o coeficiente inicial ($a_0$ ou $a_1$), é chamado de polinômio de Hermite (Hermite polynomials) $H_n(\xi)$

\[h_n(\xi) = \begin{cases} a_0 H_n(\xi), & n=2k & (k=0,1,2,\dots) \\ a_1 H_n(\xi), & n=2k+1 & (k=0,1,2,\dots) \end{cases}\]

• Estado estacionário normalizado do oscilador harmônico:

\[\psi_n(x) = \left(\frac{m\omega}{\pi\hbar} \right)^{1/4} \frac{1}{\sqrt{2^n n!}}H_n(\xi)e^{-\xi^2/2}\]

• Características do oscilador quântico
  • Funções próprias alternam entre funções pares e ímpares
  • Existe uma probabilidade não nula de encontrar a partícula em regiões classicamente proibidas (além da amplitude clássica para um dado $E$)
  • Para todos os estados estacionários com $n$ ímpar, a probabilidade de encontrar a partícula no centro é zero
  • Quanto maior o $n$, mais o oscilador quântico se assemelha ao oscilador clássico

Pré-requisitos

• Método de separação de variáveis
• Equação de Schrödinger e função de onda
• Teorema de Ehrenfest
• Equação de Schrödinger independente do tempo
• Poço quadrado infinito unidimensional
• Solução algébrica do oscilador harmônico

Configuração do modelo

Para a descrição do oscilador harmônico na mecânica clássica e a importância do problema do oscilador harmônico, consulte o artigo anterior.

Oscilador harmônico na mecânica quântica

O problema do oscilador harmônico quântico consiste em resolver a equação de Schrödinger para o potencial

\[V(x) = \frac{1}{2}m\omega^2 x^2 \label{eqn: potential_omega}\tag{1}\]

A equação de Schrödinger independente do tempo para o oscilador harmônico é

\[-\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2} + \frac{1}{2}m\omega^2x^2\psi = E\psi \label{eqn:t_independent_schrodinger_eqn}\tag{2}\]

Existem duas abordagens completamente diferentes para resolver este problema. Uma é o método analítico usando séries de potências (power series), e a outra é o método algébrico usando operadores de escada (ladder operators). Embora o método algébrico seja mais rápido e simples, também é necessário estudar a solução analítica usando séries de potências. Anteriormente, abordamos o método de solução algébrica, e aqui trataremos do método de solução analítica.

Transformação da equação de Schrödinger

Introduzindo a variável adimensional

\[\xi \equiv \sqrt{\frac{m\omega}{\hbar}}x \label{eqn:xi}\tag{3}\]

podemos reescrever a equação de Schrödinger independente do tempo ($\ref{eqn:t_independent_schrodinger_eqn}$) de forma simplificada como:

\[\frac{d^2\psi}{d\xi^2} = \left(\xi^2-K \right)\psi. \label{eqn:schrodinger_eqn_with_xi}\tag{4}\]

Aqui, $K$ é a energia expressa em unidades de $\cfrac{1}{2}\hbar\omega$.

\[K \equiv \frac{2E}{\hbar\omega}. \label{eqn:K}\tag{5}\]

Agora, precisamos resolver a equação reescrita ($\ref{eqn:schrodinger_eqn_with_xi}$). Primeiro, para $\xi$ muito grande (ou seja, para $x$ muito grande), $\xi^2 \gg K$, então

\[\frac{d^2\psi}{d\xi^2} \approx \xi^2\psi \label{eqn:schrodinger_eqn_approx}\tag{6}\]

e a solução aproximada para isso é

\[\psi(\xi) \approx Ae^{-\xi^2/2} + Be^{\xi^2/2} \label{eqn:psi_approx}\tag{7}\]

No entanto, o termo $B$ diverge quando $|x|\to \infty$ e não pode ser normalizado, então a solução assintótica fisicamente permitida é

\[\psi(\xi) \to Ae^{-\xi^2/2} \label{eqn:psi_asymp}\tag{8}\]

Agora, separando a parte exponencial, escrevemos

\[\psi(\xi) = h(\xi)e^{-\xi^2/2} \quad \text{(onde }\lim_{\xi\to\infty}h(\xi)=A\text{)} \label{eqn:psi_and_h}\tag{9}\]

Usamos o método de aproximação no processo de derivação para encontrar a forma da solução assintótica para descobrir o termo exponencial $e^{-\xi^2/2}$, mas a equação ($\ref{eqn:psi_and_h}$) obtida através disso não é uma equação aproximada, mas sim uma equação exata. Separar a forma assintótica desta maneira é o primeiro passo padrão ao resolver equações diferenciais na forma de séries de potências.

Diferenciando a equação ($\ref{eqn:psi_and_h}$) para obter $\cfrac{d\psi}{d\xi}$ e $\cfrac{d^2\psi}{d\xi^2}$, temos

\[\begin{gather*} \frac{d\psi}{d\xi} = \left(\frac{dh}{d\xi}-\xi h \right)e^{-\xi^2/2}, \\ \frac{d^2\psi}{d\xi^2} = \left(\frac{d^2h}{d\xi^2}-2\xi\frac{dh}{d\xi}+(\xi^2-1)h \right)e^{-\xi^2/2} \end{gather*}\]

portanto, a equação de Schrödinger ($\ref{eqn:schrodinger_eqn_with_xi}$) agora se torna

\[\frac{d^2h}{d\xi^2}-2\xi\frac{dh}{d\xi}+(K-1)h = 0 \label{eqn:schrodinger_eqn_with_h}\tag{10}\]

Expansão em série de potências

Pelo teorema de Taylor, qualquer função que varia suavemente pode ser expressa como uma série de potências, então vamos tentar encontrar a solução da equação ($\ref{eqn:schrodinger_eqn_with_h}$) na forma de uma série de $\xi$:

\[h(\xi) = a_0 + a_1\xi + a_2\xi^2 + \cdots = \sum_{j=0}^{\infty}a_j\xi^j \label{eqn:h_series_exp}\tag{11}\]

Diferenciando cada termo desta série, obtemos as seguintes duas equações:

\[\begin{gather*} \frac{dh}{d\xi} = a_1 + 2a_2\xi + 3a_3\xi^2 + \cdots = \sum_{j=0}^{\infty}ja_j\xi^{j-1}, \\ \frac{d^2 h}{d\xi^2} = 2a_2 + 2\cdot3a_3\xi + 3\cdot4a_4\xi^2 + \cdots = \sum_{j=0}^{\infty} (j+1)(j+2)a_{j+2}\xi^j. \end{gather*}\]

Substituindo essas duas equações de volta na equação de Schrödinger (equação [$\ref{eqn:schrodinger_eqn_with_h}$]), obtemos:

\[\sum_{j=0}^{\infty}[(j+1)(j+2)a_{j+2} - 2ja_j + (K-1)a_j]\xi^j = 0. \label{eqn:schrodinger_eqn_power_series}\tag{12}\]

Pela unicidade da expansão em série de potências, o coeficiente de cada potência de $\xi$ deve ser zero, então

\[(j+1)(j+2)a_{j+2} - 2ja_j + (K-1)a_j = 0\] \[\therefore a_{j+2} = \frac{(2j+1-K)}{(j+1)(j+2)}a_j. \label{eqn:recursion_formula}\tag{13}\]

Esta fórmula de recorrência (recursion formula) é equivalente à equação de Schrödinger. Dados dois valores arbitrários para $a_0$ e $a_1$, podemos determinar os coeficientes de todos os termos da solução $h(\xi)$.

No entanto, nem sempre é possível normalizar a solução obtida desta maneira. Se a série $\sum a_j$ for uma série infinita (se $\lim_{j\to\infty} a_j\neq0$), para $j$ muito grande, a fórmula de recorrência acima se aproxima de

\[a_{j+2} \approx \frac{2}{j}a_j\]

e a solução aproximada para isso é

\[a_j \approx \frac{C}{(j/2)!} \quad \text{(}C\text{ é uma constante arbitrária)}\]

Neste caso, para grandes valores de $\xi$ onde os termos de ordem superior se tornam dominantes,

\[h(\xi) \approx C\sum\frac{1}{(j/2)!}\xi^j \approx C\sum\frac{1}{j!}\xi^{2j} \approx Ce^{\xi^2}\]

e se $h(\xi)$ tomar esta forma $Ce^{\xi^2}$, $\psi(\xi)$ na equação ($\ref{eqn:psi_and_h}$) se torna $Ce^{\xi^2/2}$, divergindo quando $\xi \to \infty$. Isso corresponde à solução não normalizável com $A=0, B\neq0$ na equação ($\ref{eqn:psi_approx}$).

Portanto, a série $\sum a_j$ deve ser finita. Deve existir um valor ‘máximo’ de $j$, $n\in \mathbb{N}$, tal que $a_j=0$ para $j>n$, e para que isso aconteça, deve-se ter $a_{n+2}=0$ para $a_n$ não nulo, então da equação ($\ref{eqn:recursion_formula}$)

\[K = 2n + 1\]

Substituindo isso na equação ($\ref{eqn:K}$), obtemos as energias fisicamente permitidas

\[E_n = \left(n+\frac{1}{2} \right)\hbar\omega, \quad n=0,1,2,\dots \label{eqn:E_n}\tag{14}\]

Assim, obtivemos a condição de quantização de energia da equação (21) da solução algébrica do oscilador harmônico usando um método completamente diferente.

Polinômios de Hermite (Hermite polynomials) $H_n(\xi)$ e estados estacionários $\psi_n(x)$

Polinômios de Hermite $H_n$

Em geral, $h_n(\xi)$ é um polinômio de grau $n$ em $\xi$, e contém apenas termos de grau par se $n$ for par, e apenas termos de grau ímpar se $n$ for ímpar. O restante, excluindo o coeficiente inicial ($a_0$ ou $a_1$), é chamado de polinômio de Hermite (Hermite polynomial) $H_n(\xi)$.

\[h_n(\xi) = \begin{cases} a_0 H_n(\xi), & n=2k & (k=0,1,2,\dots) \\ a_1 H_n(\xi), & n=2k+1 & (k=0,1,2,\dots) \end{cases}\]

Tradicionalmente, os coeficientes são arbitrariamente definidos de modo que o coeficiente do termo de maior grau de $H_n$ seja $2^n$.

Aqui estão os primeiros polinômios de Hermite:

\[\begin{align*} H_0 &= 1 \\ H_1 &= 2\xi \\ H_2 &= 4\xi^2 - 2 \\ H_3 &= 8\xi^3 - 12\xi \\ H_4 &= 16\xi^4 - 48\xi^2 + 12 \\ H_5 &= 32\xi^5 - 160\xi^3 + 120\xi \\ &\qquad\vdots \end{align*}\]

Estados estacionários $\psi_n(x)$

Os estados estacionários normalizados para o oscilador harmônico são:

\[\psi_n(x) = \left(\frac{m\omega}{\pi\hbar} \right)^{1/4} \frac{1}{\sqrt{2^n n!}}H_n(\xi)e^{-\xi^2/2}.\]

Isso coincide com o resultado obtido na solução algébrica do oscilador harmônico (equação [27]).

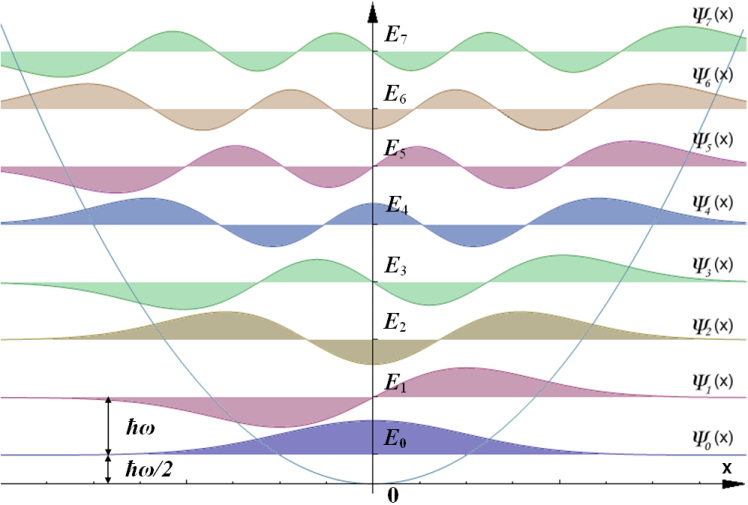
A imagem a seguir mostra os estados estacionários $\psi_n(x)$ e as densidades de probabilidade $|\psi_n(x)|^2$ para os primeiros 8 valores de $n$. Pode-se observar que as funções próprias do oscilador quântico alternam entre funções pares e ímpares.

Fonte da imagem

• Autor: Usuário do Wikimedia AllenMcC
• Licença: CC BY-SA 3.0

Fonte da imagem

• Autor: Usuário do Wikimedia AllenMcC
• Licença: Domínio Público

O oscilador quântico é bastante diferente do oscilador clássico correspondente, não apenas na quantização da energia, mas também na distribuição de probabilidade da posição $x$, que apresenta características peculiares.

• Existe uma probabilidade não nula de encontrar a partícula em regiões classicamente proibidas (além da amplitude clássica para um dado $E$)
• Para todos os estados estacionários com $n$ ímpar, a probabilidade de encontrar a partícula no centro é zero

Quanto maior o $n$, mais o oscilador quântico se assemelha ao oscilador clássico. A imagem abaixo mostra a distribuição de probabilidade clássica da posição $x$ (linha pontilhada) e o estado quântico $|\psi_{30}|^2$ (linha sólida) para $n=30$. Se suavizarmos as partes irregulares, os dois gráficos mostram uma forma aproximadamente coincidente.

Fonte da imagem

• Autor: Usuário do Wikimedia AkanoToE
• Licença: Domínio Público

Visualização Interativa das Distribuições de Probabilidade do Oscilador Quântico

A seguir está uma visualização responsiva baseada em Plotly.js que eu mesmo criei. Você pode ajustar o valor de $n$ usando o controle deslizante para verificar a forma da distribuição de probabilidade clássica e $|\psi_n|^2$ em relação à posição $x$.

• Página de visualização original: https://www.yunseo.kim/physics-visualization/quantum-harmonic-oscillator
• Código fonte: Repositório yunseo-kim/physics-visualization
• Licença: Veja aqui

Além disso, se você puder usar Python em seu próprio computador e tiver um ambiente com as bibliotecas Numpy, Plotly e Dash instaladas, você também pode executar o script Python /src/quantum_oscillator.py no mesmo repositório para ver os resultados.