Harmonic Addition Theorem

TL;DR

Harmonic Addition Theorem

• \[a\sin \theta + b\cos \theta = \sqrt{a^{2}+b^{2}} \sin(\theta+\alpha)\]

\[(\text{where}\ \cos \alpha = \frac{a}{\sqrt{a^{2}+b^{2}}},\ \sin \alpha = \frac{b}{\sqrt{a^{2}+b^{2}}})\]

• \[a\sin \theta + b\cos \theta = \sqrt{a^{2}+b^{2}} \cos(\theta-\beta)\]

\[(\text{where}\ \cos \beta = \frac{b}{\sqrt{a^{2}+b^{2}}},\ \sin \beta = \frac{a}{\sqrt{a^{2}+b^{2}}})\]

Prerequisites

• Trigonometric Addition Formulas

Harmonic Addition Theorem

For a function $f(\theta) = a \cos \theta + b \sin \theta$ in the form of a sum of trigonometric functions, there always exist real numbers $\alpha$ and $\beta$ that satisfy $f(\theta)=\sqrt{a^2+b^2} \sin(\theta+\alpha) = \sqrt{a^2+b^2} \cos(\theta-\beta)$.

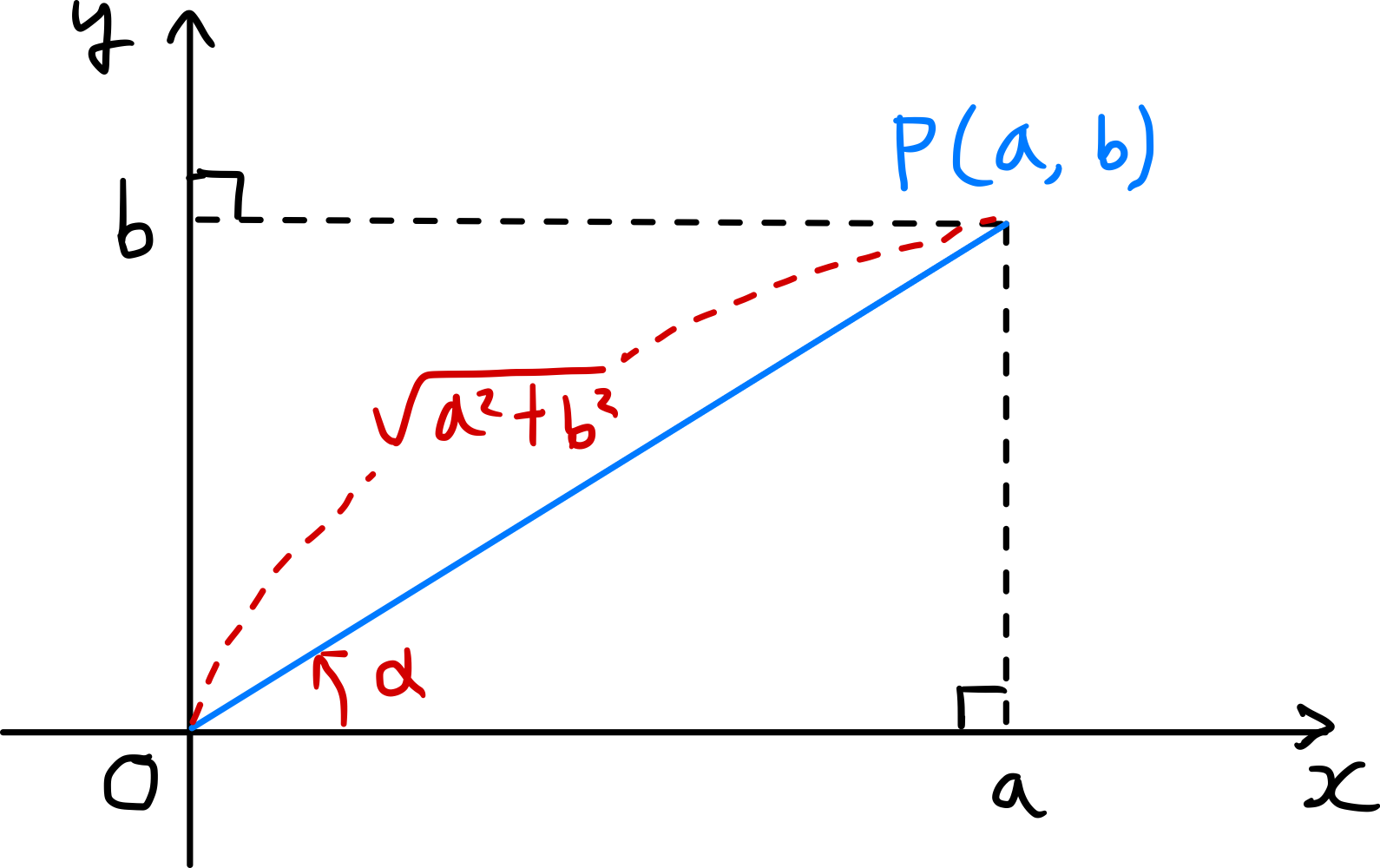
As shown in the figure, if we take a point $P(a,b)$ on the coordinate plane and let $\alpha$ be the angle formed by the line segment $\overline{OP}$ and the positive direction of the x-axis, then

\[\overline{OP} = \sqrt{a^2+b^2}\]

and

\[\cos \alpha = \frac{a}{\sqrt{a^{2} + b^{2}}},\ \sin \alpha = \frac{b}{\sqrt{a^{2} + b^{2}}} \tag{1}\]

At this time,

\[\begin{align*} a \sin \theta + b \cos \theta &= \sqrt{a^{2}+b^{2}} \left(\frac{a}{\sqrt{a^{2}+b^{2}}}\sin \theta + \frac{b}{\sqrt{a^{2}+b^{2}}}\cos \theta \right) \\ &= \sqrt{a^{2}+b^{2}}(\cos \alpha \sin \theta + \sin \alpha \cos \theta) \\ &= \sqrt{a^{2}+b^{2}} \sin(\theta + \alpha). \tag{2} \end{align*}\]

Similarly, if we take a point $P^{\prime}(b,a)$ and let $\beta$ be the angle formed by the line segment $\overline{OP^{\prime}}$ and the positive direction of the x-axis, we get:

\[a \sin \theta + b \cos \theta = \sqrt{a^{2}+b^{2}}\cos(\theta-\beta). \tag{3}\] \[\text{where}\ \cos \beta = \frac{b}{\sqrt{a^{2}+b^{2}}},\ \sin \beta = \frac{a}{\sqrt{a^{2}+b^{2}}}.\]

This transformation of a trigonometric function of the form $a \sin \theta + b \sin \theta$ into the form $r\sin(\theta+\alpha)$ or $r\cos(\theta-\beta)$ is called Harmonic Addition.

Example

Given the function $f(\theta)=-\sqrt{3}\sin \theta + \cos \left(\theta - \frac{\pi}{3} \right)$, find the maximum and minimum values of the function $f(\theta)$ in the interval $[0, 2\pi]$.

1. Transform into $a\sin\theta + b\cos\theta$ form

Using the Trigonometric Addition Formulas, we can transform the given function as follows:

\[\begin{align*} f(\theta) &= -\sqrt{3}\sin \theta + \cos \left(\theta - \frac{\pi}{3} \right) \\ &= -\sqrt{3}\sin \theta + \left( \cos\theta \cos\frac{\pi}{3} + \sin\theta \sin\frac{\pi}{3} \right) \\ &= -\frac{\sqrt{3}}{2}\sin\theta + \frac{1}{2}\cos\theta . \end{align*}\]

2. Transform into $r\sin(\theta+\alpha)$ form

Let $a=-\frac{\sqrt{3}}{2}$, $b=\frac{1}{2}$, then

\[r = \sqrt{a^2+b^2} = \sqrt{\frac{3}{4}+\frac{1}{4}} = 1\]

Also, there exists one real value $\alpha$ where $0 \leq \alpha<2\pi$ and $\cos\alpha = a$, $\sin\alpha = b$. From the trigonometric ratios of special angles, we can determine that $\alpha = \frac{5}{6}\pi$.

Therefore, transforming the given function $f(\theta)$ into $r\sin(\theta+\alpha)$ form gives:

\[f(\theta) = \sin \left(\theta + \frac{5\pi}{6} \right).\]

3. Find the maximum and minimum values in the given interval

The function $f(\theta) = \sin \left(\theta + \frac{5\pi}{6} \right)$ is a periodic function with a period of $2\pi$, and in the given interval, it has a maximum value of $1$ and a minimum value of $-1$.

\[\therefore M=1,\ m=-1\]