Energy Transfer by Collisions

TL;DR

• Total energy and momentum are conserved during collisions
• Ions that have lost all electrons and electrons themselves only possess kinetic energy
• Neutral atoms and partially ionized ions have internal energy, and can undergo excitation, deexcitation, or ionization depending on changes in potential energy
• Classification of collision types based on changes in kinetic energy before and after collision:
  • Elastic collision: Total kinetic energy remains constant before and after collision
  • Inelastic collision: Kinetic energy is lost during the collision process
    • Excitation
    • Ionization
  • Superelastic collision: Kinetic energy increases during the collision process
    • Deexcitation
• Energy transfer rate by elastic collision:
  • Energy transfer rate by individual collision: $\zeta_L = \cfrac{4m_1m_2}{(m_1+m_2)^2}\cos^2\theta_2$
  • Average energy transfer rate per collision: $\overline{\zeta_L} = \cfrac{4m_1m_2}{(m_1+m_2)^2}\overline{\cos^2\theta_2} = \cfrac{2m_1m_2}{(m_1+m_2)^2}$
    • When $m_1 \approx m_2$: $\overline{\zeta_L} \approx \cfrac{1}{2}$, effective energy transfer occurs, reaching thermal equilibrium quickly
    • When $m_1 \ll m_2$ or $m_1 \gg m_2$: $\overline{\zeta_L} \approx 10^{-5}\sim 10^{-4}$, energy transfer efficiency is very low, making it difficult to reach thermal equilibrium. This is why in weakly ionized plasmas, $T_e \gg T_i \approx T_n$, with electron temperature significantly different from ion and neutral atom temperatures.
• Energy transfer rate by inelastic collision:
  • Maximum internal energy conversion rate by single collision: $\zeta_L = \cfrac{\Delta U_\text{max}}{\cfrac{1}{2}m_1v_1^2} = \cfrac{m_2}{m_1+m_2}\cos^2\theta_2$
  • Average maximum internal energy conversion rate: $\overline{\zeta_L} = \cfrac{m_2}{m_1+m_2}\overline{\cos^2\theta_2} = \cfrac{m_2}{2(m_1+m_2)}$
    • When $m_1 \approx m_2$: $\overline{\zeta_L} \approx \cfrac{1}{4}$
    • When $m_1 \gg m_2$: $\overline{\zeta_L} \approx 10^{-5}\sim 10^{-4}$
    • When $m_1 \ll m_2$: $\overline{\zeta_L} = \cfrac{1}{2}$, most efficiently increasing the internal energy of the collision target (ion or neutral atom) to create an excited state. This is why electron-induced ionization (plasma generation), excitation (emission), and molecular dissociation (radical generation) occur readily.

Prerequisites

• Subatomic Particles and Constituents of an Atom

Particle Collisions in Plasma

• Total energy and momentum are conserved during collisions
• Ions that have lost all electrons and electrons themselves only possess kinetic energy
• Neutral atoms and partially ionized ions have internal energy, and can undergo excitation, deexcitation, or ionization depending on changes in potential energy
• Classification of collision types based on changes in kinetic energy before and after collision:
  • Elastic collision: Total kinetic energy remains constant before and after collision
  • Inelastic collision: Kinetic energy is lost during the collision process
    • Excitation
    • Ionization
  • Superelastic collision: Kinetic energy increases during the collision process
    • Deexcitation

Energy Transfer by Elastic Collision

Energy Transfer Rate by Individual Collision

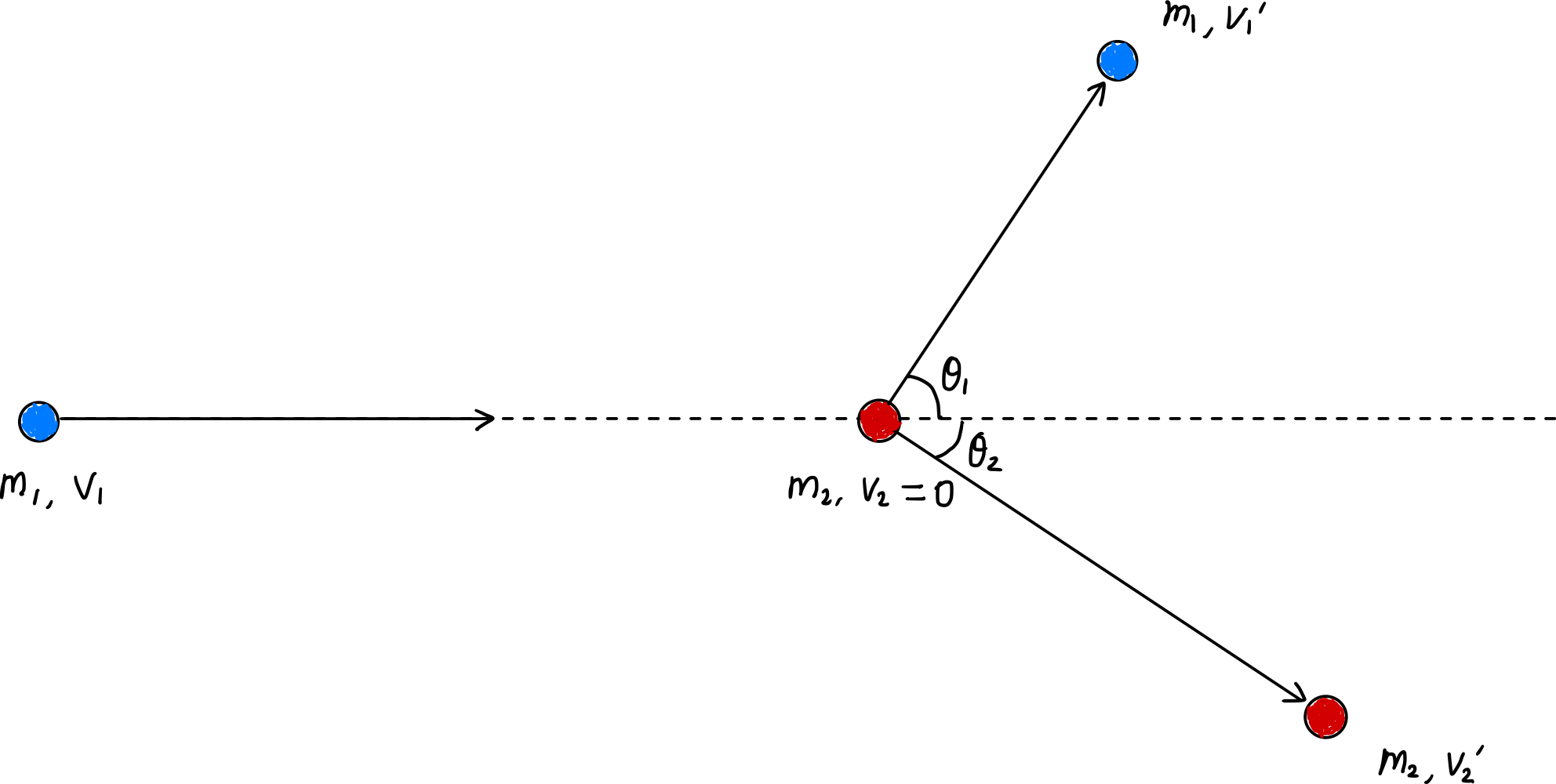
In elastic collisions, momentum and kinetic energy are conserved before and after the collision.

Writing momentum conservation equations for the x-axis and y-axis respectively:

\[\begin{gather*} m_1v_1 = m_1v_1^{\prime}\cos\theta_1 + m_2v_2^{\prime}\cos\theta_2, \label{eqn:momentum_conservation_x}\tag{1} \\ m_1v_1^{\prime}\sin\theta_1 = m_2v_2^{\prime}\sin\theta_2 \label{eqn:momentum_conservation_y}\tag{2} \end{gather*}\]

Also, due to energy conservation:

\[\frac{1}{2}m_1v_1^2 = \frac{1}{2}m_1{v_1^{\prime}}^2 + \frac{1}{2}m_2{v_2^{\prime}}^2\] \[v_1^2 = {v_1^{\prime}}^2 + \frac{m_2}{m_1}{v_2^{\prime}}^2 \label{eqn:energy_conservation}\tag{3}\]

From equation ($\ref{eqn:momentum_conservation_x}$):

\[m_1 v_1^{\prime} \cos \theta_1 = m_1v_1 - m_2v_2^{\prime} \cos \theta_2 \label{eqn:momentum_conservation_x_2}\tag{4}\]

Squaring both sides of equations ($\ref{eqn:momentum_conservation_y}$) and ($\ref{eqn:momentum_conservation_x_2}$) and adding them:

\[\begin{align*} (m_1v_1^{\prime})^2 &= (m_2 v_2^\prime \sin \theta_2)^2 + (m_1 v_1 - m_2 v_2^\prime \cos \theta_2)^2 \\ &= m_1^2 v_1^2 - 2 m_1 m_2 v_1 v_2^\prime \cos \theta_2 + m_2^2 {v_2^\prime}^2 \tag{5} \end{align*}\]

Now, dividing both sides by $m_1^2$:

\[{v_1^{\prime}}^2 = v_1^2 - 2 \frac{m_2}{m_1} v_1 v_2^\prime \cos \theta_2 + \left(\frac{m_2}{m_1}\right)^2 {v_2^\prime}^2 \label{eqn:momentum_conservation}\tag{6}\]

Substituting equation ($\ref{eqn:energy_conservation}$) here, we can simplify as follows:

\[\begin{gather*} \left( \frac{m_2}{m_1} \right) {v_2^\prime}^2 = 2 \left( \frac{m_2}{m_1} \right) v_1 v_2^\prime \cos \theta_2 - \left( \frac{m_2}{m_1} \right)^2 {v_2^\prime}^2 \\ 2v_1 \cos \theta_2 = \left(\frac{m_1 + m_2}{m_1} \right) v_2^\prime \\ v_2^{\prime} = \frac{2m_1v_1\cos\theta_2}{m_1 + m_2}. \label{eqn:v_2_prime}\tag{7} \end{gather*}\]

From this, we obtain the energy transfer rate $\zeta_L$ as follows:

\[\begin{align*} \therefore \zeta_L &= \frac{\cfrac{1}{2}m_2{v_2^\prime}^2}{\cfrac{1}{2}m_1v_1^2} = \frac{m_2}{m_1v_1^2} {\left(\frac{2m_1v_1\cos\theta_2}{m_1 + m_2} \right)}^2 \\ &= \frac{4m_1m_2}{(m_1+m_2)^2}\cos^2\theta_2. \quad \blacksquare \label{eqn:elastic_E_transfer_rate}\tag{8} \end{align*}\]

Average Energy Transfer Rate per Collision

For angles from $0$ to $2\pi$, $\sin^2{\theta_2}+\cos^2{\theta_2}=1$ and $\overline{\sin^2{\theta_2}}=\overline{\cos^2{\theta_2}}$, so:

\[\begin{align*} \overline{\cos^2{\theta_2}} &= \overline{(1-\sin^2{\theta_2})} = 1 - \overline{\sin^2{\theta_2}} \\ &= 1 - \overline{\cos^2{\theta_2}} \end{align*}\] \[\begin{gather*} 2 \cdot \overline{\cos^2{\theta_2}} = 1 \\ \overline{\cos^2{\theta_2}} = \frac{1}{2}. \end{gather*}\]

Substituting this into equation ($\ref{eqn:elastic_E_transfer_rate}$) we derived earlier:

\[\overline{\zeta_L} = \frac{4m_1m_2}{(m_1+m_2)^2}\overline{\cos^2\theta_2} = \frac{2m_1m_2}{(m_1+m_2)^2}. \quad \blacksquare \label{eqn:elastic_E_mean_transfer_rate}\tag{9}\]

When $m_1 \approx m_2$

This applies to electron-electron, ion-ion, neutral atom-neutral atom, and ion-neutral atom collisions. In such cases:

\[\overline{\zeta_L} = \frac{2m_1m_2}{(m_1+m_2)^2} \approx \frac{1}{2} \label{eqn:elastic_similar_m}\tag{10}\]

Effective energy transfer occurs, leading to rapid thermal equilibrium.

When $m_1 \ll m_2$ or $m_1 \gg m_2$

This applies to electron-ion, electron-neutral atom, ion-electron, and neutral atom-electron collisions. In such cases:

\[\overline{\zeta_L} = \frac{2m_1m_2}{(m_1+m_2)^2} \approx \frac{2m_1}{m_2}\text{ (based on }m_1 \ll m_2 \text{)} \approx 10^{-5}\sim 10^{-4} \label{eqn:elastic_different_m}\tag{11}\]

The energy transfer efficiency is very low, making it difficult to reach thermal equilibrium. This is why in weakly ionized plasmas, $T_e \gg T_i \approx T_n$, with electron temperature significantly different from ion and neutral atom temperatures.

Energy Transfer by Inelastic Collision

Maximum Internal Energy Conversion Rate by Single Collision

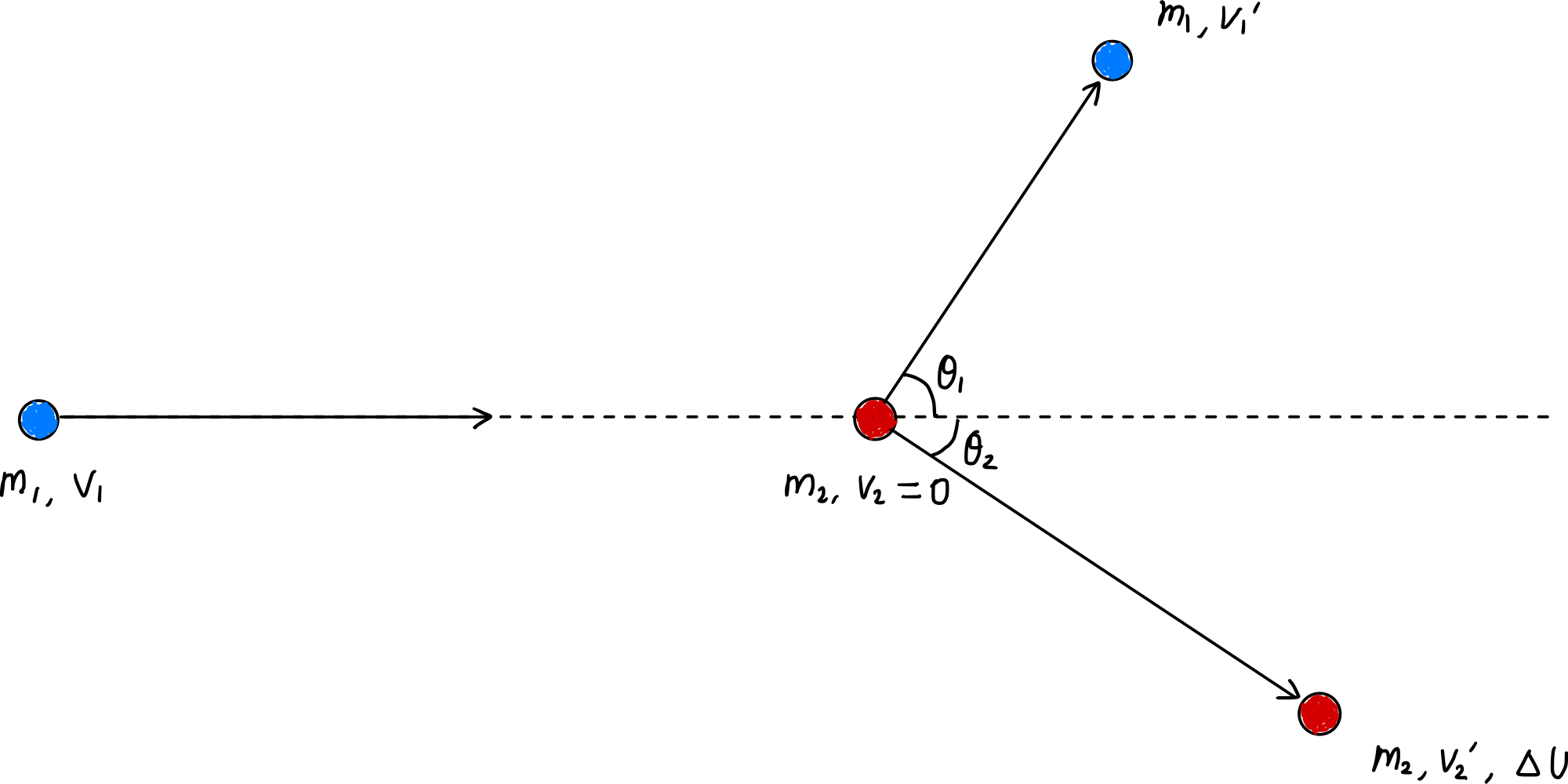
Momentum conservation (equation [$\ref{eqn:momentum_conservation}$]) still applies in this case, but kinetic energy is not conserved due to inelastic collision. In this case, the kinetic energy lost by inelastic collision is converted to internal energy $\Delta U$, so:

\[\Delta U = \frac{1}{2} m_1 v_1^2 - \left( \frac{1}{2} m_1 {v_1^{\prime}}^2 + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right) \label{eqn:delta_U}\tag{12}\]

Now, substituting equation ($\ref{eqn:momentum_conservation}$) here and simplifying, we get:

\(\begin{align*} \Delta U &= \frac{1}{2} m_1 v_1^2 - \left[ \frac{1}{2} m_1 \left( v_1^2 - 2 \frac{m_2}{m_1} v_1 v_2^{\prime} \cos \theta_2 + \left( \frac{m_2}{m_1} v_2^{\prime} \right)^2 \right) + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right] \\ &= \frac{1}{2} m_1 v_1^2 - \left[ \frac{1}{2} m_1 v_1^2 - m_2 v_1 v_2^{\prime} \cos \theta_2 + \frac{1}{2} \frac{m_2^2}{m_1} {v_2^{\prime}}^2 + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right] \\ &= m_2 v_1 v_2^{\prime} \cos \theta_2 - \frac{1}{2}m_2{v_2^{\prime}}^2\left(\frac{m_1 + m_2}{m_1}\right) \label{eqn:delta_U_2}\tag{13} \end{align*}\).

Differentiating $\Delta U$ with respect to $v_2^\prime$, finding the extremum where the derivative is 0, and calculating the maximum value at that point:

\[\cfrac{d \Delta U}{d v_2^{\prime}} = m_2 v_1 \cos \theta_2 - m_2 v_2^{\prime} \left( \frac{m_1 + m_2}{m_1} \right) = 0 \tag{14}\] \[\begin{gather*} v_2^{\prime} \left( \frac{m_1 + m_2}{m_1} \right) = v_1 \cos \theta_2 \\ v_2^\prime = \frac{m_1v_1\cos\theta_2}{m_1+m_2}. \end{gather*}\] \[\therefore v_2^{\prime} = \frac{m_1v_1\cos\theta_2}{m_1+m_2} \text{when } \Delta U_\text{max} = \frac{1}{2}\frac{m_1m_2 v_1^2 \cos^2\theta_2}{m_1 + m_2}. \label{eqn:delta_U_max}\tag{15}\]

From this, the maximum conversion rate $\zeta_L$ from kinetic energy to internal energy possible by a single inelastic collision is:

\[\zeta_L = \frac{\Delta U_\text{max}}{\cfrac{1}{2}m_1v_1^2} = \frac{m_2}{m_1+m_2}\cos^2\theta_2. \quad \blacksquare \label{eqn:inelastic_E_transfer_rate}\tag{16}\]

Average Maximum Internal Energy Conversion Rate

Similarly, substituting $\overline{\cos^2{\theta_2}} = \cfrac{1}{2}$ into equation ($\ref{eqn:inelastic_E_transfer_rate}$), we get:

\[\overline{\zeta_L} = \frac{m_2}{m_1+m_2}\overline{\cos^2\theta_2} = \frac{m_2}{2(m_1+m_2)}. \label{eqn:inelastic_E_mean_transfer_rate}\tag{17}\]

When $m_1 \approx m_2$

This applies to ion-ion, ion-neutral atom, and neutral atom-neutral atom collisions.

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} = \frac{1}{4}. \label{eqn:inelastic_similar_m}\tag{18}\]

When $m_1 \gg m_2$

This applies to ion-electron and neutral atom-electron collisions.

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} \approx \frac{m_2}{2m_1} \approx 10^{-5}\sim 10^{-4}. \label{eqn:inelastic_ion_electron}\tag{19}\]

When $m_1 \ll m_2$

This applies to electron-ion and electron-neutral atom collisions. While the first two cases were not significantly different from elastic collisions, this third case shows an important difference. In this case:

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} \approx \frac{m_2}{2m_2} = \frac{1}{2} \label{eqn:inelastic_electron_ion}\tag{20}\]

This is the most efficient way to increase the internal energy of the collision target (ion or neutral atom) to create an excited state. This is why, as we will discuss later, electron-induced ionization (plasma generation), excitation (emission), and molecular dissociation (radical generation) occur readily.