Continuous and Characteristic X Rays

TL;DR

• bremsstrahlung (breaking radiation): Continuous spectrum X-rays emitted when charged particles like electrons are accelerated by electrical forces while passing near atomic nuclei
• Minimum wavelength: $\lambda_\text{min} = \cfrac{hc}{E_\text{max}} = \cfrac{12400 \text{[Å}\cdot\text{eV]}}{V\text{[eV]}}$
• characteristic X-ray: Discontinuous spectrum X-rays emitted when an electron from an outer shell transitions to fill a vacancy in an inner shell created by an incident electron ionizing the atom, with energy equal to the difference between the two energy levels

Prerequisites

• Subatomic Particles and Constituents of an Atom

Discovery of X-rays

Röntgen discovered that X-rays are produced when electron beams are irradiated onto a target. Since it was not known at the time that X-rays were electromagnetic waves, they were named X-rays to indicate their unknown nature, and are also called Röntgen radiation after their discoverer.

The image above shows a simplified structure of a typical X-ray tube. Inside the X-ray tube, a cathode made of tungsten filament and an anode with a fixed target are sealed in vacuum. When tens of kV of high voltage is applied between the electrodes, electrons are emitted from the cathode and irradiated onto the target at the anode, producing X-rays. However, the energy conversion efficiency to X-rays is typically less than 1%, with over 99% of the energy being converted to heat, necessitating additional cooling equipment.

bremsstrahlung (braking radiation)

When charged particles like electrons pass near atomic nuclei, they are rapidly deflected and decelerated by electrical forces between the particle and nucleus, releasing energy in the form of X-rays. Since this energy conversion is not quantized, the emitted X-rays show a continuous spectrum, and this is called bremsstrahlung or braking radiation.

However, the energy of photons emitted through bremsstrahlung cannot exceed the kinetic energy of the incident electrons. Therefore, there exists a minimum wavelength for the emitted X-rays, which can be simply calculated using the following equation:

\[\lambda_\text{min} = \frac{hc}{E}. \tag{1}\]

Since Planck’s constant $h$ and speed of light $c$ are constants, this minimum wavelength is determined solely by the energy of the incident electrons. The wavelength $\lambda$ corresponding to energy of $1\text{eV}$ is approximately $1.24 \mu\text{m}=12400\text{Å}$. Therefore, the minimum wavelength $\lambda_\text{min}$ when voltage $V$ is applied to the X-ray tube is:

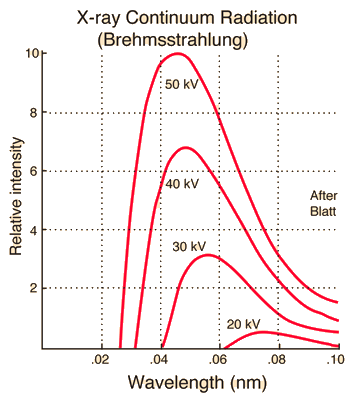
\[\lambda_\text{min} \text{[Å]} = \frac{12400 \text{[Å}\cdot\text{eV]}}{V\text{[eV]}}. \label{eqn:lambda_min}\tag{2}\]

The following graph shows continuous X-ray spectra at different voltages while maintaining constant tube current. As voltage increases, the minimum wavelength $\lambda_{\text{min}}$ decreases and the overall X-ray intensity increases.

characteristic X-ray

If the voltage applied to the X-ray tube is sufficiently high, incident electrons can collide with electrons in inner shells of target atoms, ionizing them. In this case, electrons from outer shells quickly fill the vacant positions in inner shells while releasing energy, producing X-ray photons with energy equal to the difference between the two energy levels. The spectrum of X-rays emitted through this process is discontinuous and is determined by the unique energy levels of the target atom, independent of the energy or intensity of the incident electron beam. These are called characteristic X-rays.

Siegbahn notation

Image source

• Author: English Wikipedia user HenrikMidtiby
• License: CC BY-SA 3.0

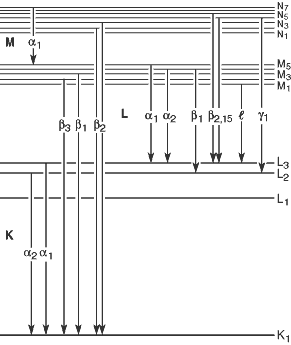
According to Siegbahn notation, X-rays emitted when electrons from L shell, M shell, … fill vacancies in K shell are designated as $K_\alpha$, $K_\beta$, … as shown in the image above. However, after the emergence of modern atomic models following Siegbahn notation, it was discovered that for multi-electron atoms, energy levels within each shell (energy levels with the same principal quantum number) differ according to other quantum numbers, leading to further subdivisions such as $K_{\alpha_1}$, $K_{\alpha_2}$, … for each $K_\alpha$, $K_\beta$, …

This traditional notation is still widely used in spectroscopy. However, due to its unsystematic nature and potential for confusion, the International Union of Pure and Applied Chemistry (IUPAC) recommends using a different notation system.

IUPAC notation

The standard notation for atomic orbitals and characteristic X-rays recommended by IUPAC is as follows. First, names are assigned to each atomic orbital according to the following table:

$n$ (principal quantum number)	$l$(azimuthal quantum number)	$s$(spin quantum number)	$j$(total angular momentum quantum number)	Atomic orbital	X-ray notation
$1$	$0$	$\pm1/2$	$1/2$	$1s_{1/2}$	$K_{(1)}$
$2$	$0$	$\pm1/2$	$1/2$	$2s_{1/2}$	$L_1$
$2$	$1$	$-1/2$	$1/2$	$2p_{1/2}$	$L_2$
$2$	$1$	$+1/2$	$3/2$	$2p_{3/2}$	$L_3$
$3$	$0$	$\pm1/2$	$1/2$	$3s_{1/2}$	$M_1$
$3$	$1$	$-1/2$	$1/2$	$3p_{1/2}$	$M_2$
$3$	$1$	$+1/2$	$3/2$	$3p_{3/2}$	$M_3$
$3$	$2$	$-1/2$	$3/2$	$3d_{3/2}$	$M_4$
$3$	$2$	$+1/2$	$5/2$	$3d_{5/2}$	$M_5$
$4$	$0$	$\pm1/2$	$1/2$	$4s_{1/2}$	$N_1$
$4$	$1$	$-1/2$	$1/2$	$4p_{1/2}$	$N_2$
$4$	$1$	$+1/2$	$3/2$	$4p_{3/2}$	$N_3$
$4$	$2$	$-1/2$	$3/2$	$4d_{3/2}$	$N_4$
$4$	$2$	$+1/2$	$5/2$	$4d_{5/2}$	$N_5$
$4$	$3$	$-1/2$	$5/2$	$4f_{5/2}$	$N_6$
$4$	$3$	$+1/2$	$7/2$	$4f_{7/2}$	$N_7$

Total angular momentum quantum number $j=|l+s|$.

Characteristic X-rays emitted when an electron transitions from a higher energy level to a lower energy level are designated according to the following rule:

\[\text{(X-ray notation of final energy level)-(X-ray notation of initial energy level)}\]

For example, characteristic X-rays emitted when an electron transitions from $2p_{1/2}$ orbital to $1s_{1/2}$ is called $\text{K-L}_2$.

X-ray Spectrum

The above shows the X-ray spectrum emitted when electron beams accelerated at 60kV are irradiated onto a rhodium (Rh) target. A smooth and continuous curve due to bremsstrahlung appears, and according to equation ($\ref{eqn:lambda_min}$), X-rays are emitted only for wavelengths above approximately $0.207\text{Å} = 20.7\text{pm}$. The sharp peaks appearing throughout the graph are due to the characteristic K-shell X-rays of rhodium atoms. As mentioned earlier, since each target atom has its own characteristic X-ray spectrum, the constituent elements of a target can be determined by examining the wavelengths at which spikes are observed in the X-ray spectrum when electron beams are irradiated onto the target.

Lower energy X-rays such as $L_\alpha, L_\beta, \dots$ are also emitted in addition to $K_\alpha, K_\beta, \dots$. However, these have much lower energies and are typically absorbed by the X-ray tube housing before reaching the detector.