삼각함수의 합성(Harmonic Addition Theorem)

TL;DR

삼각함수의 합성 (Harmonic Addition Theorem)

• \[a\sin \theta + b\cos \theta = \sqrt{a^{2}+b^{2}} \sin(\theta+\alpha)\]

\[(단,\ \cos \alpha = \frac{a}{\sqrt{a^{2}+b^{2}}},\ \sin \alpha = \frac{b}{\sqrt{a^{2}+b^{2}}})\]

• \[a\sin \theta + b\cos \theta = \sqrt{a^{2}+b^{2}} \cos(\theta-\beta)\]

\[(단,\ \cos \beta = \frac{b}{\sqrt{a^{2}+b^{2}}},\ \sin \beta = \frac{a}{\sqrt{a^{2}+b^{2}}})\]

Prerequisites

• 삼각함수의 덧셈정리

삼각함수의 합성 (Harmonic Addition Theorem)

$f(\theta) = a \cos \theta + b \sin \theta$와 같이 삼각함수의 합의 형태로 이뤄진 함수 $f(\theta)$에 대해, $f(\theta)=\sqrt{a^2+b^2} \sin(\theta+\alpha) = \sqrt{a^2+b^2} \cos(\theta-\beta)$를 만족하는 실수 $\alpha$, $\beta$가 항상 존재한다.

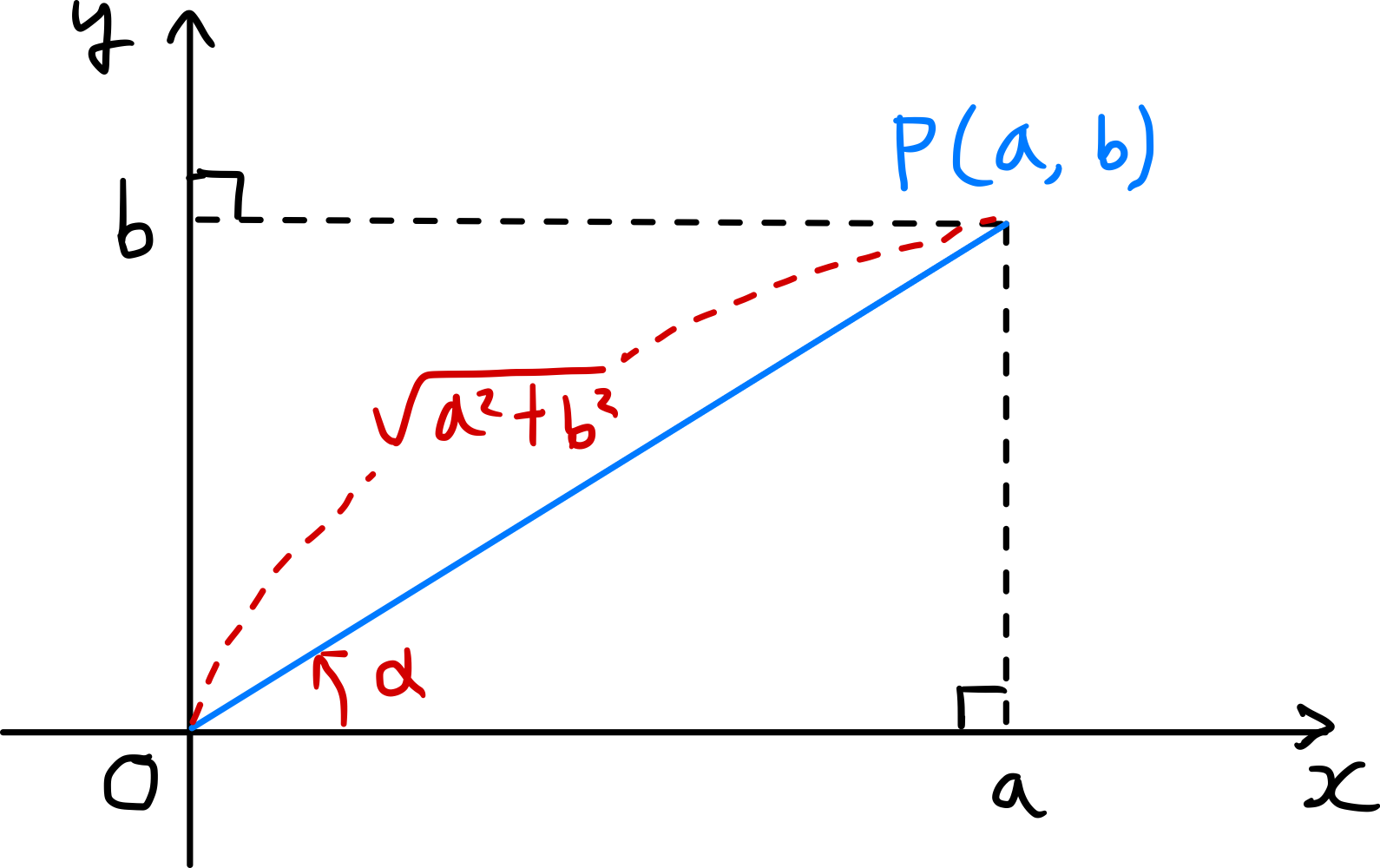
그림과 같이 좌표평면 위에 점 $P(a,b)$를 잡고 선분 $\overline{OP}$와 $x$축의 양의 방향이 이루는 각의 크기를 $\alpha$라 하면

\[\overline{OP} = \sqrt{a^2+b^2}\]

이고

\[\cos \alpha = \frac{a}{\sqrt{a^{2} + b^{2}}},\ \sin \alpha = \frac{b}{\sqrt{a^{2} + b^{2}}} \tag{1}\]

이다. 이때,

\[\begin{align*} a \sin \theta + b \cos \theta &= \sqrt{a^{2}+b^{2}} \left(\frac{a}{\sqrt{a^{2}+b^{2}}}\sin \theta + \frac{b}{\sqrt{a^{2}+b^{2}}}\cos \theta \right) \\ &= \sqrt{a^{2}+b^{2}}(\cos \alpha \sin \theta + \sin \alpha \cos \theta) \\ &= \sqrt{a^{2}+b^{2}} \sin(\theta + \alpha). \tag{2} \end{align*}\]

같은 방법으로 점 $P^{\prime}(b,a)$를 잡고 선분 $\overline{OP^{\prime}}$과 $x$축의 양의 방향이 이루는 각의 크기를 $\beta$라고 하면 다음을 얻는다.

\[a \sin \theta + b \cos \theta = \sqrt{a^{2}+b^{2}}\cos(\theta-\beta). \tag{3}\] \[단,\ \cos \beta = \frac{b}{\sqrt{a^{2}+b^{2}}},\ \sin \beta = \frac{a}{\sqrt{a^{2}+b^{2}}}.\]

이와 같이 $a \sin \theta + b \sin \theta$ 꼴의 삼각함수를 $r\sin(\theta+\alpha)$ 또는 $r\cos(\theta-\beta)$ 꼴로 변형하는 것을 삼각함수의 합성(Harmonic Addition)이라고 한다.

예제

함수 $f(\theta)=-\sqrt{3}\sin \theta + \cos \left(\theta - \frac{\pi}{3} \right)$라고 할 때, 구간 $[0, 2\pi]$에서 함수 $f(\theta)$의 최댓값과 최솟값을 구해라.

1. $a\sin\theta + b\cos\theta$ 꼴로 변형

삼각함수의 덧셈정리를 이용하여 주어진 함수식을 변형하면

\[\begin{align*} f(\theta) &= -\sqrt{3}\sin \theta + \cos \left(\theta - \frac{\pi}{3} \right) \\ &= -\sqrt{3}\sin \theta + \left( \cos\theta \cos\frac{\pi}{3} + \sin\theta \sin\frac{\pi}{3} \right) \\ &= -\frac{\sqrt{3}}{2}\sin\theta + \frac{1}{2}\cos\theta . \end{align*}\]

2. $r\sin(\theta+\alpha)$ 꼴로 변형

$a=-\frac{\sqrt{3}}{2}$, $b=\frac{1}{2}$로 놓으면,

\[r = \sqrt{a^2+b^2} = \sqrt{\frac{3}{4}+\frac{1}{4}} = 1\]

이다.

또한, $0 \leq \alpha<2\pi$이고 $\cos\alpha = a$, $\sin\alpha = b$인 실수 $\alpha$ 값은 1개 존재한다. 특수각에 대한 삼각비의 값으로부터, $\alpha = \frac{5}{6}\pi$임을 알 수 있다.

따라서, 주어진 함수 $f(\theta)$를 $r\sin(\theta+\alpha)$ 꼴로 변형하면 다음과 같다.

\[f(\theta) = \sin \left(\theta + \frac{5\pi}{6} \right).\]

3. 주어진 구간에서 최댓값과 최솟값 구하기

함수 $f(\theta) = \sin \left(\theta + \frac{5\pi}{6} \right)$는 $2\pi$를 주기로 하는 주기함수이며, 주어진 구간에서 최댓값 $1$, 최솟값 $-1$을 가진다.

\[\therefore M=1,\ m=-1\]