플라즈마의 정의와 온도의 개념, 그리고 사하 방정식(Saha equation)

TL;DR

• 플라즈마(plasma): 집단적인 움직임(collective behavior)을 보이는 하전입자 및 중성입자로 구성된 준중성(quasineutral) 기체
• 플라즈마의 ‘집단적 움직임(collective behavior)’:
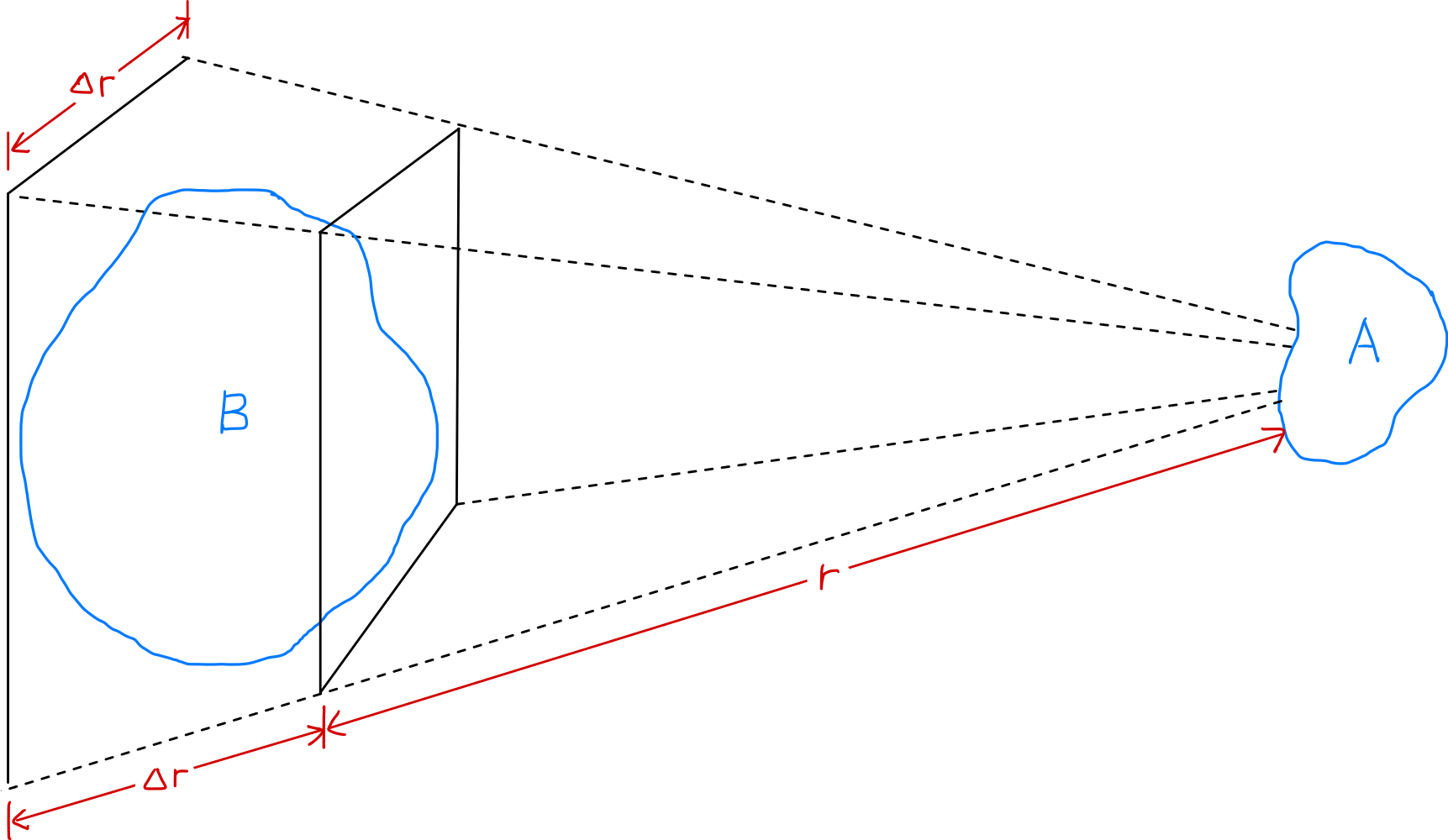
  • 플라즈마 내 두 영역 $A$와 $B$ 사이의 전기력은 거리가 증가함에 따라 $1/r^2$로 감소
  • 그러나 주어진 입체각($\Delta r/r$)이 일정할 때 $A$에 영향을 줄 수 있는 플라즈마 영역 $B$의 부피는 $r^3$으로 증가
  • 따라서 플라즈마를 구성하는 부분들은 먼 거리에서도 서로에게 유의미한 힘을 가할 수 있음
• 사하 방정식(Saha equation): 열평형 상태에 놓인 기체의 이온화 상태와 온도 및 압력 간의 관계식

\[\frac{n_{i+1}n_e}{n_i} = \frac{2}{\lambda_{\text{th}}^3}\frac{g_{i+1}}{g_i}\exp{\left[-\frac{\epsilon_{i+1}-\epsilon_i}{k_B T}\right]}\]

• 플라즈마 물리에서의 온도 개념:
  • 기체와 플라즈마에서 입자당 평균 운동에너지는 온도와 밀접한 관련이 있으며, 이 둘은 서로 교환 가능한 물리량임
  • 플라즈마 물리에서는 온도를 에너지의 단위인 $\mathrm{eV}$를 사용하여 $kT$의 값으로 나타내는 것이 관례
    • $1\mathrm{eV}=11600\mathrm{K}$
  • 플라즈마는 동시에 서로 다른 여러 온도를 가질 수 있으며, 특히 전자 온도($T_e$)와 이온 온도($T_i$)는 경우에 따라서는 크게 다를 수 있음
• 저온 플라즈마 vs. 고온 플라즈마:
  • 플라즈마 온도:
    • 저온 플라즈마: $T_e \text{(>10,000℃)} \gg T_i \approx T_g \text{(}\sim\text{100℃)}$ $\rightarrow$ 비평형 플라즈마(non-equilibrium plasma)
    • 고온(열) 플라즈마: $T_e \approx T_i \approx T_g \text{(>10,000℃)}$ $\rightarrow$ 평형 플라즈마(equilibrium plasma)
  • 플라즈마 밀도:
    • 저온 플라즈마: $n_g \gg n_i \approx n_e$ $\rightarrow$ 이온화 비율이 작고 대부분 중성 입자로 존재함
    • 고온(열) 플라즈마: $n_g \approx n_i \approx n_e $ $\rightarrow$ 이온화 비율이 큼
  • 플라즈마의 열용량:
    • 저온 플라즈마: 전자 온도는 높지만 밀도가 낮고, 대부분은 비교적 저온의 중성 입자이므로 열용량이 작아 뜨겁지 않음
    • 고온(열) 플라즈마: 전자, 이온, 중성 입자 모두 온도가 높으므로 열용량이 커 뜨거움

Prerequisites

• 아원자 입자와 원자의 구성 요소
• 맥스웰-볼츠만 분포(통계역학)
• 질량과 에너지, 입자와 파동
• 대칭성과 보존 법칙(양자역학), 겹침(degeneracy)

플라즈마의 정의

보통 비전공자를 대상으로 플라즈마를 설명하는 글에서는 플라즈마를 다음과 같이 정의한다.

구성 원자들이 전자와 양이온으로 분리되어 이온화될 때까지 기체를 가열하여 초고온 상태로 만듦으로써 얻는, 고체, 액체, 기체에 이은 물질의 제4의 상태

결코 틀린 말은 아니며, 한국핵융합에너지연구원(Korea Institute of Fusion Energy) 홈페이지에서도 이와 같이 소개하고 있다. 플라즈마에 대해 검색했을 때 쉽게 접할 수 있는 대중적인 정의이기도 하다.

다만, 위의 표현은 분명 맞는 말이긴 하지만 엄밀한 정의라고는 할 수 없다. 우리 주변의 상온 상압 환경에서의 기체도 극도로 작은 비율이기는 하지만 일부 이온화되어 있는데, 그렇다고 해서 이것을 플라즈마라고 하지는 않는다. 염화나트륨과 같은 이온결합 물질을 물에 용해시키면 전하를 띈 이온들로 분리되지만, 이러한 용액 또한 플라즈마는 아니다.
즉, 플라즈마가 물질의 이온화된 상태인 것은 맞지만, 이온화되었다고 해서 모두 플라즈마라 할 수는 없다.

보다 엄밀하게, 플라즈마는 다음과 같이 정의할 수 있다.

플라즈마는 집단적인 움직임을 보이는 하전입자 및 중성입자로 구성된 준중성 기체이다.
A plasma is a quasineutral gas of charged and neutral particles which exhibits collective behavior.

by Fransis F. Chen

‘준중성(quasineutrality)’이 무엇을 의미하는지는 추후 디바이 차폐(Debye shielding)를 다루면서 알아볼 것이다. 여기서는 플라즈마의 ‘집단적인 움직임(collective behavior)’이 어떤 의미인지 알아보자.

플라즈마의 집단적 움직임

중성 입자로 구성된 비이온화 기체의 경우, 각 기체 분자는 전기적 중성이므로 작용하는 알짜 전자기력은 $0$이며 중력의 영향 또한 무시할 수 있다. 분자는 다른 분자와 충돌하기 전까지는 방해받지 않고 움직이며, 분자 간의 충돌이 입자의 운동을 결정한다. 설령 일부 입자가 이온화되어 전하를 띈다 하더라도, 전체 기체 중 이온화된 입자의 비율이 매우 낮기 때문에 이러한 하전 입자의 전기적 영향력은 거리에 따라 $1/r^2$로 감쇠되어 먼 거리까지 미치지 못한다.

그러나 하전 입자를 다수 포함하는 플라즈마에서는 상황이 완전히 달라진다. 하전 입자들의 이동에 의해 양전하 또는 음전하의 국소적인 집중이 발생할 수 있으며 이로 인해 전기장이 발생한다. 또한 전하의 이동은 전류를 만들고, 전류는 자기장을 만든다. 이러한 전기장과 자기장은 입자 간의 충돌 없이도 멀리 떨어진 다른 입자들에게까지 영향을 미칠 수 있다.

약간의 전하를 띄는 두 플라즈마 영역 $A$와 $B$ 사이에 작용하는 전기력의 세기가 거리 $r$에 따라 어떻게 달라질지 살펴보자. $A$와 $B$ 사이의 쿨롱 법칙에 따른 전기력(Coulomb force)은 거리가 증가함에 따라 $1/r^2$로 감소한다. 그러나 주어진 입체각($\Delta r/r$)이 일정할 때, $A$에 영향을 줄 수 있는 플라즈마 영역 $B$의 부피는 $r^3$으로 증가한다. 따라서 플라즈마를 구성하는 부분들은 먼 거리에서도 서로에게 유의미한 힘을 가할 수 있다. 이처럼 먼 거리까지 작용하는 전기력은 플라즈마가 매우 다양한 운동 양상을 보일 수 있게 하며, 플라즈마 물리(plasma physics)라는 하나의 독립된 학문 분야가 존재하는 이유이기도 하다. ‘집단적 움직임(collective behavior)’이란 이렇게 어느 한 영역의 운동이 해당 영역에서의 국소적인 조건뿐만 아니라 멀리 떨어진 다른 영역의 플라즈마 상태에도 영향을 받음을 의미한다.

사하 방정식 (Saha equation)

사하 방정식(Saha equation)은 열평형 상태에 놓인 기체의 이온화 상태와 온도 및 압력 간의 관계식으로, 인도의 천체물리학자 메그나드 사하(Meghnad Saha)가 고안하였다.

\[\frac{n_{i+1}n_e}{n_i} = \frac{2}{\lambda_{\text{th}}^3}\frac{g_{i+1}}{g_i}\exp{\left[-\frac{\epsilon_{i+1}-\epsilon_i}{k_B T}\right]} \label{eqn:saha_eqn}\tag{1}\]

• $n_i$: $i$가 양이온($i$개의 전자를 잃은 양이온)의 밀도
• $g_i$: $i$가 양이온의 상태 겹침(degeneracy)
• $\epsilon_i$: 중성 원자에서 $i$개의 전자를 떼어내어 $i$가 양이온을 만드는 데 필요한 에너지
  • $\epsilon_{i+1}-\epsilon_i$: $(i+1)$차 이온화 에너지
• $n_e$: 전자 밀도
• $k_B$: 볼츠만 상수
• $\lambda_{\text{th}}$: 열적 드브로이 파장(주어진 온도에서 기체 내 전자의 평균 드브로이 파장)

\[\lambda_{\text{th}} \equiv \frac{h}{\sqrt{2\pi m_e k_B T}} \quad \text{ (}h\text{: 플랑크 상수)} \label{eqn:lambda_th}\tag{2}\]

• $m_e$: 전자 질량
• $T$: 기체의 온도

만약 한 단계의 이온화만이 중요하며, 2가 이상의 양이온의 생성은 무시할 수 있는 경우라면 $n_1=n_i=n_e$, $n_0=n_n$, $U_i = \epsilon = \epsilon_1$, $i=0$으로 놓고 다음과 같이 단순화할 수 있다.

\[\begin{align*} \frac{n_i^2}{n_n} &= \frac{2}{\lambda_{th}^3}\frac{g_1}{g_0}\exp{\left[-\frac{\epsilon}{k_B T} \right]} \label{eqn:saha_eqn_approx}\tag{3}\\ &= 2\left(\frac{2\pi m_e k_B T}{h^2}\right)^{3/2}\frac{g_1}{g_0}e^{-U_i/{k_B T}} \\ &= 2\frac{g_1}{g_0}\left(\frac{2\pi m_e k_B}{h^2}\right)^{3/2}T^{3/2}e^{-U_i/{k_B T}}. \label{eqn:saha_eqn_approx_2}\tag{4} \end{align*}\]

상온 상압 환경에서 공기(질소)의 이온화 비율

위 식에서 $2 \cfrac{g_1}{g_0}$의 값은 기체의 성분마다 달라지지만, 많은 경우 이 값의 크기 자릿수(order of magnitude)는 $1$이다. 따라서 대략적으로 다음과 같이 근사할 수 있다.

\[\frac{n_i^2}{n_n} \approx \left(\frac{2\pi m_e k_B}{h^2}\right)^{3/2} T^{3/2} e^{-U_i/{k_B T}}.\]

SI 단위계에서 기본 상수 $m_e$, $k_B$, $h$의 값은 각각

• $m_e \approx 9.11 \times 10^{-31} \mathrm{kg}$
• $k_B \approx 1.38 \times 10^{-23} \mathrm{J/K}$
• $h \approx 6.63 \times 10^{-34} \mathrm{J \cdot s}$

이며, 이를 위 식에 대입하면 다음을 얻는다.

\[\frac{n_i^2}{n_n} \approx 2.4 \times 10^{21}\ T^{3/2} e^{-U_i/{k_B T}}. \label{eqn:fractional_ionization}\tag{5}\]

이로부터, 상온 상압 환경($n_n \approx 3 \times 10^{25} \mathrm{m^{-3}}$, $T\approx 300\mathrm{K}$)의 질소($U_i \approx 14.5\mathrm{eV} \approx 2.32 \times 10^{-18}\mathrm{J}$)에 대하여 이온화 비율 $n_i/(n_n + n_i) \approx n_i/n_n$의 근사값을 계산하면

\[\frac{n_i}{n_n} \approx 10^{-122}\]

으로 극도로 낮은 비율임을 알 수 있다. 이것이 우주 환경에서와 달리 지표면과 해수면 근처의 대기 환경에서 자연적으로는 플라즈마를 거의 접할 수 없는 이유이다.

플라즈마 물리에서의 온도 개념

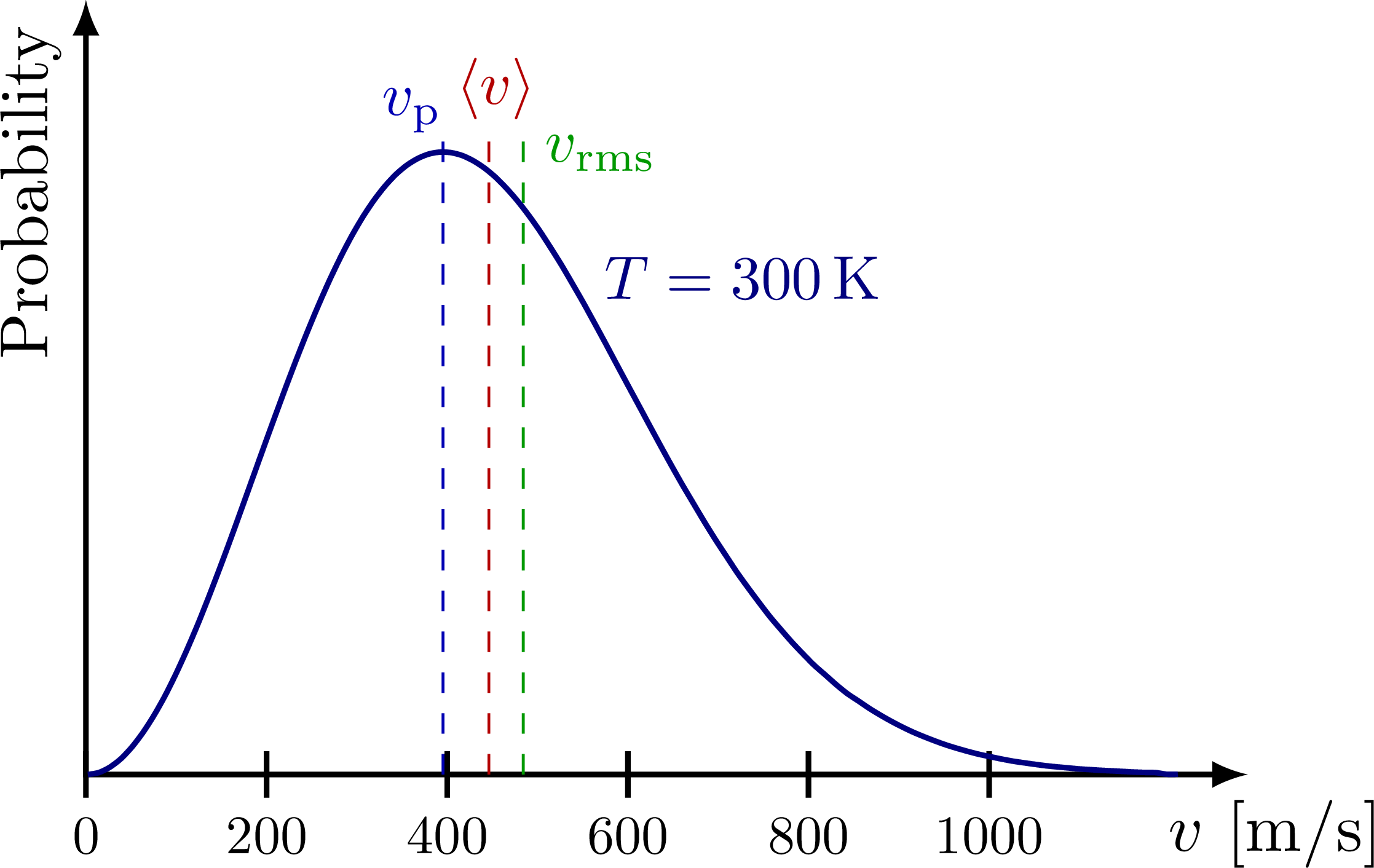
열평형 상태의 기체를 구성하는 입자들의 속력은 대체로 다음과 같은 맥스웰-볼츠만 분포(Maxwell–Boltzmann distribution)를 따른다.

\[f(v) = \left(\frac{m}{2\pi k_B T} \right)^{3/2} 4\pi v^2 \exp{\left(-\frac{mv^2}{2k_B T} \right)} \label{eqn:maxwell_boltzmann_dist}\tag{6}\]

이미지 출처

• 저작자: TikZ.net author Izaak Neutelings
• 라이선스: CC BY-SA 4.0

• 최빈 속력(most probable speed): $v_p = \sqrt{\cfrac{2k_B T}{m}}$
• 평균 속력(mean speed): $\langle v \rangle = \sqrt{\cfrac{8k_B T}{\pi m}}$
• 제곱평균제곱근 속력(RMS speed): $v_{rms} = \sqrt{\langle v^2 \rangle} = \sqrt{\cfrac{3k_B T}{m}}$

온도 $T$에서 입자 하나당 갖는 평균 운동에너지는 $\cfrac{1}{2}m\langle v^2 \rangle = \cfrac{1}{2}mv_{rms}^2 = \cfrac{3}{2}k_B T$(자유도 $3$ 기준)로 온도에 의해서만 결정된다. 이처럼 기체와 플라즈마에서 입자당 평균 운동에너지는 온도와 밀접한 관련이 있으며, 이 둘은 서로 교환 가능한 물리량이므로 플라즈마 물리에서는 온도를 에너지의 단위인 $\mathrm{eV}$로 나타내는 것이 관례이다. 차원 수의 혼동을 피하기 위해 평균 운동에너지 $\langle E_k \rangle$ 대신 $kT$의 값으로 온도를 나타낸다.

$kT=1\mathrm{eV}$일 때의 온도 $T$는

\[\begin{align*} T\mathrm{[K]} &= \frac{1.6 \times 10^{-19}\mathrm{[J]}}{1.38 \times 10^{-23}\mathrm{[J/K]}} \\ &= 11600\mathrm{[K]} \end{align*} \label{eqn:temp_conv_factor}\tag{7}\]

이므로, 플라즈마 물리에서 온도를 나타낼 경우 $1\mathrm{eV}=11600\mathrm{K}$을 의미한다.
ex) 온도가 $2\mathrm{eV}$인 플라즈마의 $kT$ 값은 $2\mathrm{eV}$이며, 입자당 평균 운동에너지는 $\cfrac{3}{2}kT=3\mathrm{eV}$이다.

또한 플라즈마는 동시에 여러 온도를 가질 수 있다. 플라즈마에서는 이온끼리의 충돌 또는 전자끼리의 충돌 빈도가 전자와 이온 사이의 충돌 빈도보다 크며, 이 때문에 전자와 이온은 각각 서로 다른 온도(전자 온도 $T_e$와 이온 온도 $T_i$)에서 열평형에 도달하여 별도의 맥스웰-볼츠만 분포를 이룰 수 있고 경우에 따라서는 전자 온도와 이온 온도가 크게 다를 수 있다. 심지어는, 외부에서 자기장 $\vec{B}$가 가해질 경우, 같은 종류의 입자(e.g. 이온)라도 운동 방향이 자기장에 평행한지 수직인지에 따라 받는 로런츠 힘(Lorentz force)의 세기가 다르므로 서로 다른 온도 $T_\perp$와 $T_\parallel$을 가질 수 있다.

온도, 압력과 밀도 사이의 관계

이상기체 법칙에 따르면

\[PV = \left(\frac{N}{N_A}\right)RT = NkT \label{eqn:ideal_gas_law}\tag{8}\]

이며, 이로부터

\[\begin{gather*} P = \frac{NkT}{V} = nkT, \\ n = \frac{P}{kT} \end{gather*} \label{eqn:relation_between_T_P_n}\tag{9}\]

이다. 즉, 플라즈마의 밀도는 온도($kT$)에 반비례하고 압력($P$)에는 비례한다.

플라즈마의 분류: 저온 플라즈마 vs. 고온 플라즈마

Low-temperature non-thermal cold plasma	Low-temperature thermal cold plasma	High-temperature hot plasma
$T_i \approx T \approx 300 \mathrm{K}$ $T_i \ll T_e \leqslant 10^5 \mathrm{K}$	$T_i \approx T_e \approx T < 2 \times 10^4 \mathrm{K}$	$T_i \approx T_e > 10^6 \mathrm{K}$
Low pressure($\sim 100\mathrm{Pa}$) glow and arc	Arcs at $100\mathrm{kPa}$ ($1\mathrm{atm}$)	Kinetic plasma, fusion plasma

플라즈마 온도

전자 온도를 $T_e$, 이온 온도를 $T_i$, 중성 입자 온도를 $T_g$라고 할 때,

• 저온 플라즈마: $T_e \mathrm{(>10,000 K)} \gg T_i \approx T_g \mathrm{(\sim 100 K)}$ $\rightarrow$ 비평형 플라즈마(non-equilibrium plasma)
• 고온(열) 플라즈마: $T_e \approx T_i \approx T_g \mathrm{(>10,000 K)}$ $\rightarrow$ 평형 플라즈마(equilibrium plasma)

이다.

플라즈마 밀도

전자 밀도를 $n_e$, 이온 밀도를 $n_i$, 중성 입자 밀도를 $n_g$라고 할 때,

• 저온 플라즈마: $n_g \gg n_i \approx n_e$ $\rightarrow$ 이온화 비율이 작고 대부분 중성 입자로 존재함
• 고온(열) 플라즈마: $n_g \approx n_i \approx n_e $ $\rightarrow$ 이온화 비율이 큼

이다.

플라즈마의 열용량 (얼마나 뜨거운가?)

• 저온 플라즈마: 전자 온도는 높지만 밀도가 낮고, 대부분은 비교적 저온의 중성 입자이므로 열용량이 작아 뜨겁지 않음
• 고온(열) 플라즈마: 전자, 이온, 중성 입자 모두 온도가 높으므로 열용량이 커 뜨거움