조화진동자(The Harmonic Oscillator)의 해석적 풀이

TL;DR

• 진폭이 충분히 작다면 어떠한 진동도 단순조화진동(simple harmonic oscillation)으로 근사할 수 있으며, 이 덕에 단순조화진동은 물리학에서 중요한 의미 가짐
• 조화진동자: $V(x) = \cfrac{1}{2}kx^2 = \cfrac{1}{2}m\omega^2 x^2$
• 무차원 변수 $\xi$와 $\cfrac{1}{2}\hbar\omega$ 단위로 나타낸 에너지 $K$ 도입:
  • $\xi \equiv \sqrt{\cfrac{m\omega}{\hbar}}x$
  • $K \equiv \cfrac{2E}{\hbar\omega}$
  • $ \cfrac{d^2\psi}{d\xi^2} = \left(\xi^2-K \right)\psi $
• $|\xi|^2 \to \infty$일 때 물리적으로 허용된 점근해는 $\psi(\xi) \to Ae^{-\xi^2/2}$이므로,

\[\begin{gather*} \psi(\xi) = h(\xi)e^{-\xi^2/2} \quad \text{(단, }\lim_{\xi\to\infty}h(\xi)=A\text{)}, \\ \frac{d^2h}{d\xi^2}-2\xi\frac{dh}{d\xi}+(K-1)h = 0 \end{gather*}\]

• 위 방정식의 해를 급수 형태 $ h(\xi) = a_0 + a_1\xi + a_2\xi^2 + \cdots = \sum_{j=0}^{\infty}a_j\xi^j$로 표현하면,

\[a_{j+2} = \frac{(2j+1-K)}{(j+1)(j+2)}a_j\]

• 이 해가 규격화되기 위해서는 급수 $\sum a_j$는 유한해야 하며, 즉 어떤 ‘가장 큰’ $j$값 $n\in \mathbb{N}$이 존재하여 $j>n$일 때 $a_j=0$이어야 하므로
  • $ K = 2n + 1 $
  • $ E_n = \left(n+\cfrac{1}{2} \right)\hbar\omega, \quad n=0,1,2,\dots $
• 일반적으로 $h_n(\xi)$는 $\xi$의 $n$차 다항식이며, 여기서 앞의 계수($a_0$ 또는 $a_1$)을 제외한 나머지를 에르미트 다항식(Hermite polynomials) $H_n(\xi)$라고 함

\[h_n(\xi) = \begin{cases} a_0 H_n(\xi), & n=2k & (k=0,1,2,\dots) \\ a_1 H_n(\xi), & n=2k+1 & (k=0,1,2,\dots) \end{cases}\]

• 조화진동자의 규격화된 정상상태:

\[\psi_n(x) = \left(\frac{m\omega}{\pi\hbar} \right)^{1/4} \frac{1}{\sqrt{2^n n!}}H_n(\xi)e^{-\xi^2/2}\]

• 양자진동자의 특징
  • 고유함수로 짝함수와 홀함수가 번갈아 나타남
  • 고전역학적으로는 존재할 수 없는 영역(주어진 $E$에 대한 고전적인 진폭보다 큰 $x$)에서도 발견될 확률이 $0$이 아니며, 낮은 확률이지만 입자가 존재할 수 있음
  • $n$이 홀수인 모든 정상상태에 대해 중심에서 입자를 발견할 확률은 $0$
  • $n$이 클수록 고전적 진동자와 유사해짐

Prerequisites

• 변수분리법
• 슈뢰딩거 방정식과 파동함수
• 에렌페스트 정리
• 시간에 무관한 슈뢰딩거 방정식
• 1차원 무한 사각 우물
• 조화진동자의 대수적 풀이

모델 설정

고전역학에서의 조화진동자 기술 방식과, 조화진동자 문제가 갖는 중요성에 대해서는 앞선 글을 참고하라.

양자역학에서의 조화진동자

양자역학적 조화진동자 문제는 퍼텐셜

\[V(x) = \frac{1}{2}m\omega^2 x^2 \label{eqn: potential_omega}\tag{1}\]

에 대한 슈뢰딩거 방정식을 푸는 것이다. 조화진동자에 대한 시간에 무관한 슈뢰딩거 방정식은

\[-\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2} + \frac{1}{2}m\omega^2x^2\psi = E\psi \label{eqn:t_independent_schrodinger_eqn}\tag{2}\]

이다.

이 문제를 푸는 데에는 완전히 다른 두 가지 접근 방식이 있다. 하나는 거듭제곱급수(power series)를 이용한 해석적인 방법(analytic method)이고, 다른 하나는 사다리연산자(ladder operators)를 이용한 대수적인 방법(algebraic method)이다. 대수적인 방법이 더 빠르고 간단하지만, 거듭제곱급수를 이용한 해석적인 풀이 또한 공부할 필요가 있다. 앞서 대수적인 풀이 방법을 다룬 바 있으며, 여기서는 해석적인 풀이 방법을 다룬다.

슈뢰딩거 방정식의 변형

무차원의 변수

\[\xi \equiv \sqrt{\frac{m\omega}{\hbar}}x \label{eqn:xi}\tag{3}\]

를 도입하면 시간에 무관한 슈뢰딩거 방정식 ($\ref{eqn:t_independent_schrodinger_eqn}$)을 다음과 같이 간단히 쓸 수 있다.

\[\frac{d^2\psi}{d\xi^2} = \left(\xi^2-K \right)\psi. \label{eqn:schrodinger_eqn_with_xi}\tag{4}\]

여기서 $K$는 $\cfrac{1}{2}\hbar\omega$ 단위로 나타낸 에너지이다.

\[K \equiv \frac{2E}{\hbar\omega}. \label{eqn:K}\tag{5}\]

이제 이렇게 다시 쓴 방정식 ($\ref{eqn:schrodinger_eqn_with_xi}$)를 풀면 된다. 우선 매우 큰 $\xi$에 대해서(즉 매우 큰 $x$에 대해서) $\xi^2 \gg K$이므로,

\[\frac{d^2\psi}{d\xi^2} \approx \xi^2\psi \label{eqn:schrodinger_eqn_approx}\tag{6}\]

가 되며 이에 대한 근사적인 해는

\[\psi(\xi) \approx Ae^{-\xi^2/2} + Be^{\xi^2/2} \label{eqn:psi_approx}\tag{7}\]

이다. 그런데 여기서 $B$ 항은 $|x|\to \infty$일 때 발산하여 규격화할 수 없으므로, 물리적으로 허용되는 점근해는

\[\psi(\xi) \to Ae^{-\xi^2/2} \label{eqn:psi_asymp}\tag{8}\]

이다. 이제 여기서 지수 부분을 분리하여

\[\psi(\xi) = h(\xi)e^{-\xi^2/2} \quad \text{(단, }\lim_{\xi\to\infty}h(\xi)=A\text{)} \label{eqn:psi_and_h}\tag{9}\]

로 쓰자.

지수항 $e^{-\xi^2/2}$을 알아내기 위하여 유도 과정에서 근사법을 이용해 점근해의 형태를 찾았을 뿐, 이를 통해 얻어낸 식 ($\ref{eqn:psi_and_h}$)는 근사적인 식이 아니라 정확한 식이다. 이와 같이 점근 형태를 분리하는 것은 미분방정식을 거듭제곱급수 형태로 풀 때 사용하는 표준적인 첫 단계이다.

식 ($\ref{eqn:psi_and_h}$)를 미분하여 $\cfrac{d\psi}{d\xi}$와 $\cfrac{d^2\psi}{d\xi^2}$을 구하면

\[\begin{gather*} \frac{d\psi}{d\xi} = \left(\frac{dh}{d\xi}-\xi h \right)e^{-\xi^2/2}, \\ \frac{d^2\psi}{d\xi^2} = \left(\frac{d^2h}{d\xi^2}-2\xi\frac{dh}{d\xi}+(\xi^2-1)h \right)e^{-\xi^2/2} \end{gather*}\]

이므로 슈뢰딩거 방정식 ($\ref{eqn:schrodinger_eqn_with_xi}$)는 이제

\[\frac{d^2h}{d\xi^2}-2\xi\frac{dh}{d\xi}+(K-1)h = 0 \label{eqn:schrodinger_eqn_with_h}\tag{10}\]

가 된다.

거듭제곱급수 전개

테일러 정리(Taylor’s theorem)에 의하면 임의의 부드럽게 변하는 함수는 거듭제곱급수로 표현할 수 있으므로, 식 ($\ref{eqn:schrodinger_eqn_with_h}$)의 해를 $\xi$의 급수 형태인

\[h(\xi) = a_0 + a_1\xi + a_2\xi^2 + \cdots = \sum_{j=0}^{\infty}a_j\xi^j \label{eqn:h_series_exp}\tag{11}\]

형태로 구해 보자. 이 급수의 각 항을 미분하면 다음 두 식을 얻는다.

\[\begin{gather*} \frac{dh}{d\xi} = a_1 + 2a_2\xi + 3a_3\xi^2 + \cdots = \sum_{j=0}^{\infty}ja_j\xi^{j-1}, \\ \frac{d^2 h}{d\xi^2} = 2a_2 + 2\cdot3a_3\xi + 3\cdot4a_4\xi^2 + \cdots = \sum_{j=0}^{\infty} (j+1)(j+2)a_{j+2}\xi^j. \end{gather*}\]

이 두 식을 다시 슈뢰딩거 방정식(식 [$\ref{eqn:schrodinger_eqn_with_h}$])에 대입하면 다음을 얻는다.

\[\sum_{j=0}^{\infty}[(j+1)(j+2)a_{j+2} - 2ja_j + (K-1)a_j]\xi^j = 0. \label{eqn:schrodinger_eqn_power_series}\tag{12}\]

거듭제곱급수 전개의 유일성에 의해 $\xi$의 각 차수에 대한 계수는 $0$이 되어야 하므로

\[(j+1)(j+2)a_{j+2} - 2ja_j + (K-1)a_j = 0\] \[\therefore a_{j+2} = \frac{(2j+1-K)}{(j+1)(j+2)}a_j. \label{eqn:recursion_formula}\tag{13}\]

이 되풀이 공식(recursion formula)은 슈뢰딩거 방정식과 동등하다. 두 개의 임의의 상수 $a_0$와 $a_1$이 주어지면 해 $h(\xi)$의 모든 항의 계수를 구할 수 있다.

그러나 이렇게 얻은 해를 항상 규격화할 수 있는 것은 아니다. 만약 급수 $\sum a_j$가 무한급수일 경우($\lim_{j\to\infty} a_j\neq0$일 경우) 매우 큰 $j$에 대해 위의 되풀이 공식은 근사적으로

\[a_{j+2} \approx \frac{2}{j}a_j\]

가 되며, 이에 대한 근사적인 해는

\[a_j \approx \frac{C}{(j/2)!} \quad \text{(}C\text{는 임의의 상수)}\]

이다. 이 경우 고차항이 지배적이게 되는 큰 $\xi$값에 대하여

\[h(\xi) \approx C\sum\frac{1}{(j/2)!}\xi^j \approx C\sum\frac{1}{j!}\xi^{2j} \approx Ce^{\xi^2}\]

의 형태가 되며, 이렇게 $h(\xi)$가 $Ce^{\xi^2}$꼴이 되면 식 ($\ref{eqn:psi_and_h}$)의 $\psi(\xi)$는 $Ce^{\xi^2/2}$ 꼴이 되어 $\xi \to \infty$일 때 발산한다. 이는 식 ($\ref{eqn:psi_approx}$)에서 $A=0, B\neq0$인 규격화할 수 없는 해에 해당한다.

따라서 급수 $\sum a_j$는 유한해야 한다. 어떤 ‘가장 큰’ $j$값 $n\in \mathbb{N}$이 존재하여 $j>n$일 때 $a_j=0$이어야 하며, 이렇게 되기 위해서는 $0$이 아닌 $a_n$에 대하여 $a_{n+2}=0$이어야 하므로 식 ($\ref{eqn:recursion_formula}$)으로부터

\[K = 2n + 1\]

이어야 한다. 이를 식 ($\ref{eqn:K}$)에 대입하면 물리적으로 허용된 에너지

\[E_n = \left(n+\frac{1}{2} \right)\hbar\omega, \quad n=0,1,2,\dots \label{eqn:E_n}\tag{14}\]

를 얻는다. 이로써 조화진동자의 대수적 풀이의 식 (21)에서의 에너지의 양자화 조건을 전혀 다른 방법을 이용하여 동일하게 얻었다.

에르미트 다항식 (Hermite polynomials) $H_n(\xi)$와 정상상태 $\psi_n(x)$

에르미트 다항식 $H_n$

일반적으로 $h_n(\xi)$는 $\xi$의 $n$차 다항식이고, $n$이 짝수이면 짝수 차수만, $n$이 홀수이면 홀수 차수만 포함한다. 여기서 앞의 계수($a_0$ 또는 $a_1$)을 제외한 나머지를 에르미트 다항식(Hermite polynomials) $H_n(\xi)$라고 한다.

\[h_n(\xi) = \begin{cases} a_0 H_n(\xi), & n=2k & (k=0,1,2,\dots) \\ a_1 H_n(\xi), & n=2k+1 & (k=0,1,2,\dots) \end{cases}\]

전통적으로 $H_n$의 최고차항의 계수가 $2^n$이 되도록 임의로 계수를 정한다.

다음은 에르미트 다항식의 처음 몇 개를 나타낸 것이다.

\[\begin{align*} H_0 &= 1 \\ H_1 &= 2\xi \\ H_2 &= 4\xi^2 - 2 \\ H_3 &= 8\xi^3 - 12\xi \\ H_4 &= 16\xi^4 - 48\xi^2 + 12 \\ H_5 &= 32\xi^5 - 160\xi^3 + 120\xi \\ &\qquad\vdots \end{align*}\]

정상상태 $\psi_n(x)$

조화진동자에 대한 규격화된 정상상태는 다음과 같다.

\[\psi_n(x) = \left(\frac{m\omega}{\pi\hbar} \right)^{1/4} \frac{1}{\sqrt{2^n n!}}H_n(\xi)e^{-\xi^2/2}.\]

이는 조화진동자의 대수적 풀이에서 구한 결과(식 [27])와 일치한다.

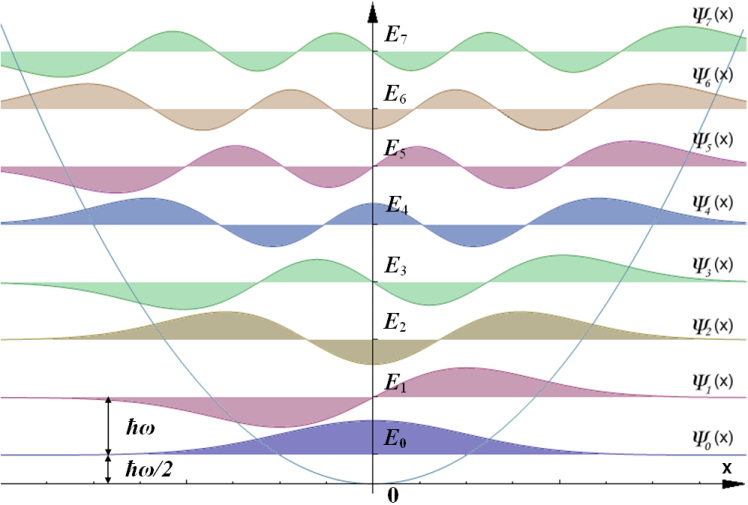
다음 이미지는 첫 8개의 $n$값에 대한 정상상태 $\psi_n(x)$와 확률밀도 $|\psi_n(x)|^2$을 나타낸 것이다. 양자진동자의 고유함수로 짝함수와 홀함수가 번갈아 나타남을 볼 수 있다.

이미지 출처

• 저작자: 위키미디어 유저 AllenMcC
• 라이선스: CC BY-SA 3.0

이미지 출처

• 저작자: 위키미디어 유저 AllenMcC
• 라이선스: Public Domain

양자진동자는 대응하는 고전적 진동자와 상당히 다르며, 에너지가 양자화된 것뿐만 아니라 위치 $x$의 확률분포 또한 기묘한 특성들을 보인다.

• 고전역학적으로는 존재할 수 없는 영역(주어진 $E$에 대한 고전적인 진폭보다 큰 $x$)에서도 발견될 확률이 $0$이 아니며, 낮은 확률이지만 입자가 존재할 수 있음
• $n$이 홀수인 모든 정상상태에 대해 중심에서 입자를 발견할 확률은 $0$

$n$이 클수록 양자진동자는 고전적 진동자와 유사한 양상을 띄게 된다. 아래 이미지는 위치 $x$의 고전적인 확률분포(점선)와 $n=30$일 때의 양자상태 $|\psi_{30}|^2$(실선)을 나타낸 것이다. 울퉁불퉁한 부분들을 부드럽게 이으면 두 그래프는 대략 일치하는 형태를 보인다.

이미지 출처

• 저작자: 위키미디어 유저 AkanoToE
• 라이선스: Public Domain

Interactive Visualization of Quantum Oscillator Probability Distributions

다음은 내가 직접 작성한 Plotly.js 기반의 반응형 시각화이다. 슬라이더로 $n$값을 조절해 가며 위치 $x$에 대한 고전적인 확률분포 및 $|\psi_n|^2$의 개형을 확인할 수 있다.

• 원본 시각화 페이지: https://www.yunseo.kim/physics-visualization/quantum-harmonic-oscillator
• 소스코드: yunseo-kim/physics-visualization 리포지터리
• 라이선스: See here

또한, 만약 본인 컴퓨터에서 Python을 사용할 수 있고 Numpy, Plotly, Dash 라이브러리가 설치된 환경이라면 동일한 리포지터리 내 /src/quantum_oscillator.py Python 스크립트를 실행하여 결과를 볼 수도 있다.