自由粒子（The Free Particle）

TL;DR

• 自由粒子: $V(x)=0$、境界条件なし（任意のエネルギー）
• 変数分離した解 $\Psi_k(x,t) = Ae^{i\left(kx-\frac{\hbar k^2}{2m}t \right)}$は二乗積分すると無限大に発散するため規格化できず、これは以下を示唆する
  • 自由粒子は定常状態として存在できない
  • 自由粒子はエネルギーを正確な一つの値として定義できない（エネルギー不確実性が存在）
• それにもかかわらず、時間依存シュレーディンガー方程式の一般解は変数分離した解の線形結合であるため、変数分離した解は依然として数学的に重要な意味を持つ。ただし、この場合制限条件がないため、一般解は離散変数$n$に対する和（$\sum$）ではなく連続変数$k$に対する積分（$\int$）の形となる。
• シュレーディンガー方程式の一般解:

\[\begin{gather*} \Psi(x,t) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{i(kx-\frac{\hbar k^2}{2m}t)}dk, \\ \text{ここで }\phi(k) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\Psi(x,0)e^{-ikx}dx \end{gather*}\]

• 位置不確実性と運動量不確実性の関係:
  • 位置不確実性が小さくなると運動量不確実性は大きくなり、逆に運動量不確実性が小さくなると位置不確実性が大きくなる
  • つまり、量子力学的に自由粒子の位置と運動量を同時に正確に知ることは不可能である
• 波動関数$\Psi(x,t)$の位相速度と群速度:
  • 位相速度: $v_\text{phase} = \cfrac{\omega}{k} = \cfrac{\hbar k}{2m}$
  • 群速度: $v_\text{group} = \cfrac{d\omega}{dk} = \cfrac{\hbar k}{m}$
• 群速度の物理的意味および古典力学との比較:
  • 物理的に群速度は該当粒子の運動速度を意味する
  • $\phi(k)$がある値$k_0$近傍で非常に鋭い形であると仮定した場合（運動量不確実性が十分小さい場合）、

\[v_\text{group} = v_\text{classical} = \sqrt{\cfrac{2E}{m}}\]

Prerequisites

• オイラーの公式
• フーリエ変換（Fourier transform）& プランシュレルの定理（Plancherel’s theorem）
• シュレーディンガー方程式と波動関数
• 時間に依存しないシュレーディンガー方程式
• 1次元無限井戸

モデル設定

最も単純な場合である自由粒子（$V(x)=0$）を考察しよう。古典的にはこれは単なる等速度運動に過ぎないが、量子力学ではこの問題はより興味深い。
自由粒子に対する時間に依存しないシュレーディンガー方程式は

\[-\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2}=E\psi \tag{1}\]

つまり

\[\frac{d^2\psi}{dx^2} = -k^2\psi \text{、ここで }k\equiv \frac{\sqrt{2mE}}{\hbar} \label{eqn:t_independent_schrodinger_eqn}\tag{2}\]

である。ここまではポテンシャルが$0$である無限井戸内部と同じである。ただし今回は一般解を次の指数関数形で書こう。

\[\psi(x) = Ae^{ikx} + Be^{-ikx}. \tag{3}\]

$Ae^{ikx} + Be^{-ikx}$と$C\cos{kx}+D\sin{kx}$は同じ$x$の関数を表す等価な方法である。オイラーの公式$e^{ix}=\cos{x}+i\sin{x}$により

\[\begin{align*} Ae^{ikx}+Be^{-ikx} &= A[\cos{kx}+i\sin{kx}] + B[\cos{(-kx)}+i\sin{(-kx)}] \\ &= A(\cos{kx}+i\sin{kx}) + B(\cos{kx}-i\sin{kx}) \\ &= (A+B)\cos{kx} + i(A-B)\sin{kx}. \end{align*}\]

つまり、$C=A+B$、$D=i(A-B)$とおくと

\[Ae^{ikx} + Be^{-ikx} = C\cos{kx}+D\sin{kx}. \blacksquare\]

逆に$A$と$B$を$C$と$D$で表すと$A=\cfrac{C-iD}{2}$、$B=\cfrac{C+iD}{2}$である。

量子力学で$V=0$の場合、指数関数は移動する波動を表し、自由粒子を扱う際に最も便利である。一方、正弦・余弦関数は定在波を表すのに適しており、無限井戸の場合に自然に現れる。

無限井戸とは異なり、今回は$k$と$E$を制限する境界条件がない。つまり自由粒子は任意の正のエネルギーを持つことができる。

変数分離した解と位相速度

$\psi(x)$に時間依存性$e^{-iEt/\hbar}$を付けると

\[\Psi(x,t) = Ae^{ik\left(x-\frac{\hbar k}{2m}t \right)} + Be^{-ik\left(x+\frac{\hbar k}{2m}t \right)} \label{eqn:Psi_seperated_solution}\tag{4}\]

を得る。

このような特別な形$(x\pm vt)$に依存する$x$と$t$に関する任意の関数は、形が変わらずに速度$v$で$\mp x$方向に移動する波動を表す。したがって式($\ref{eqn:Psi_seperated_solution}$)の第一項は右に移動する波動を表し、第二項は同じ波長と進行速度を持ち振幅のみが異なる波動が左に移動することを表す。これらは$k$の符号のみが異なるため

\[\Psi_k(x,t) = Ae^{i\left(kx-\frac{\hbar k^2}{2m}t \right)} \tag{5}\]

と書くことができ、この時$k$の符号による波動の進行方向は次のようになる。

\[k \equiv \pm\frac{\sqrt{2mE}}{\hbar},\quad \begin{cases} k>0 \Rightarrow & \text{右に移動}, \\ k<0 \Rightarrow & \text{左に移動}. \end{cases} \tag{6}\]

自由粒子の「定常状態」は明らかに進行波であり*、その波長は$\lambda = 2\pi/|k|$でド・ブロイの公式（de Broglie formula）により

\[p = \frac{2\pi\hbar}{\lambda} = \hbar k \label{eqn:de_broglie_formula}\tag{7}\]

の運動量を持つ。

*「定常状態」なのに進行波だというのは物理的には当然矛盾である。理由はすぐに分かる。

また、この波動の速度は次のようになる。

\[v_{\text{phase}} = \left|\frac{\omega}{k}\right| = \frac{\hbar|k|}{2m} = \sqrt{\frac{E}{2m}}. \label{eqn:phase_velocity}\tag{8}\]

（ここで$\omega$は$t$の前の係数$\cfrac{\hbar k^2}{2m}$である。）

しかし、この波動関数は二乗積分すると無限大に発散するため規格化できない。

\[\int_{-\infty}^{\infty}\Psi_k^*\Psi_k dx = |A|^2\int_{-\infty}^{\infty}dx = \infty. \tag{9}\]

つまり、自由粒子の場合、変数分離した解は物理的に可能な状態ではない。 自由粒子は定常状態として存在できず、ある特定のエネルギー値を持つこともできない。実際、直感的に考えても両端に境界条件が全くないのに定在波が形成される方がおかしい。

時間依存シュレーディンガー方程式の一般解$\Psi(x,t)$を求める

それにもかかわらず、この変数分離した解は依然として重要な意味を持つ。物理的解釈とは別に、時間依存シュレーディンガー方程式の一般解は変数分離した解の線形結合であるという数学的意味を持つからである。ただし、この場合制限条件がないため、一般解は離散変数$n$に対する和（$\sum$）ではなく連続変数$k$に対する積分（$\int$）の形を持つ。

\[\Psi(x,t) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{i(kx-\frac{\hbar k^2}{2m}t)}dk. \label{eqn:Psi_general_solution}\tag{10}\]

ここで$\cfrac{1}{\sqrt{2\pi}}\phi(k)dk$が「時間に依存しないシュレーディンガー方程式」投稿の式(21)での$c_n$と同じ役割を果たす。

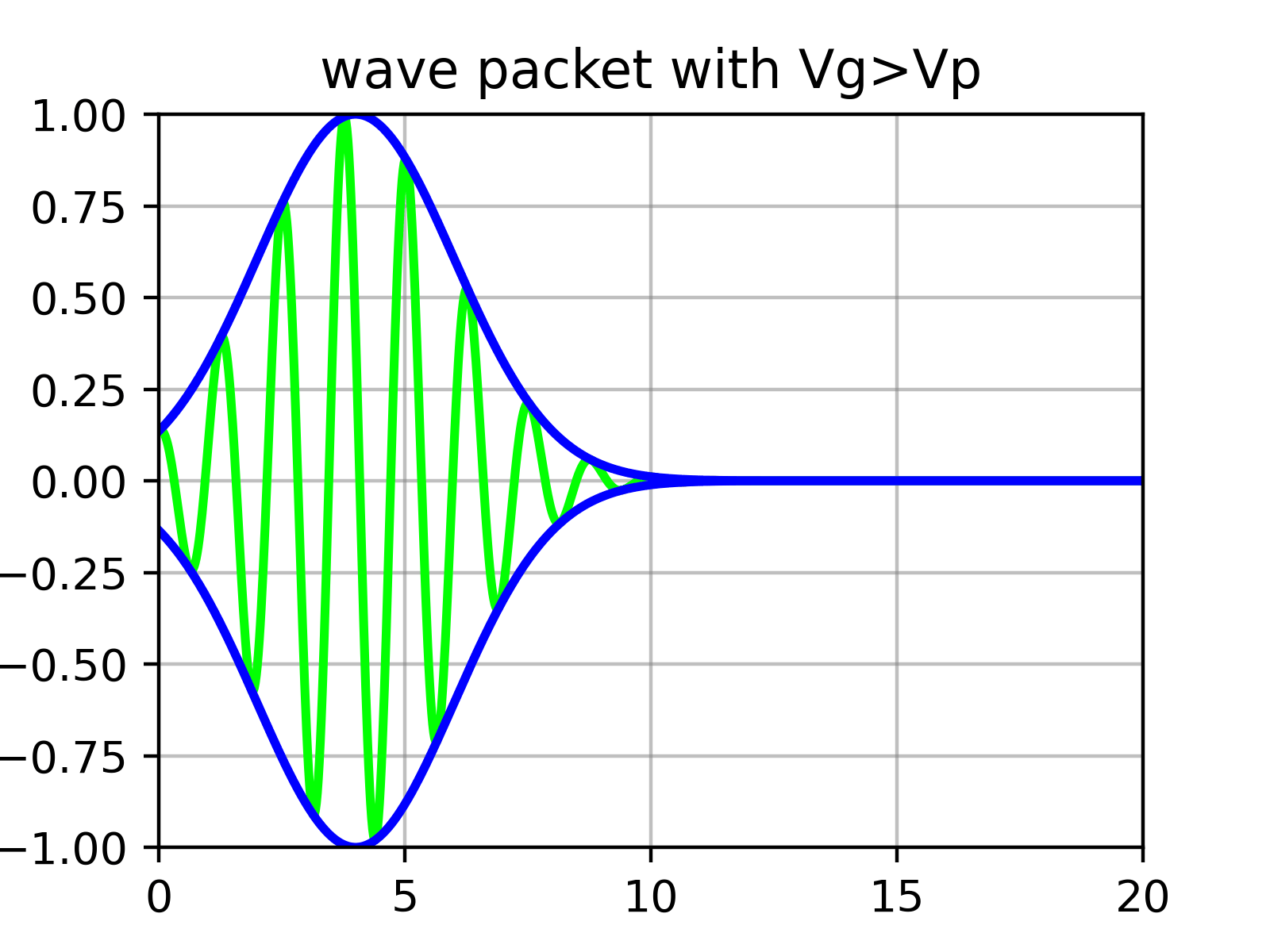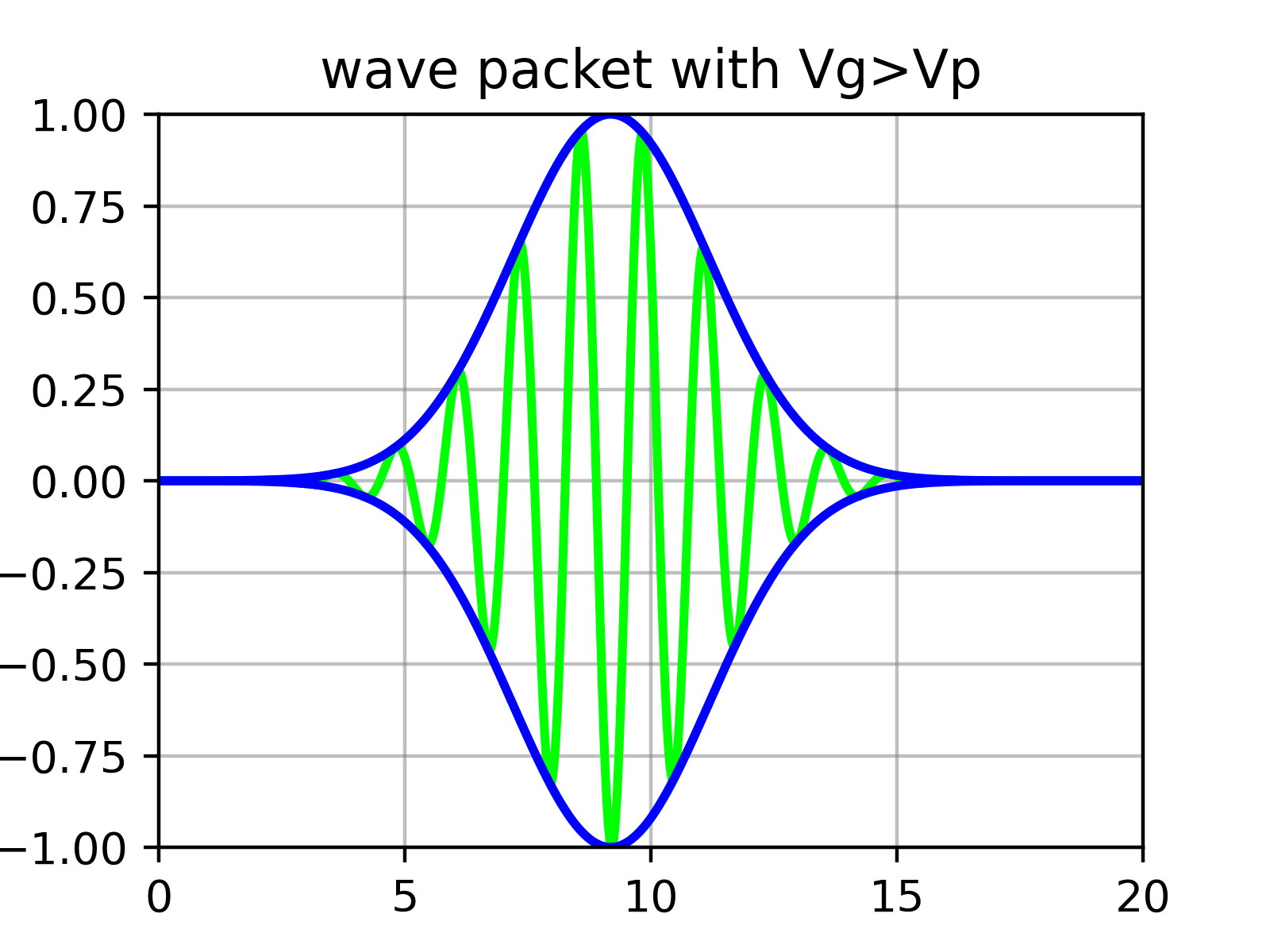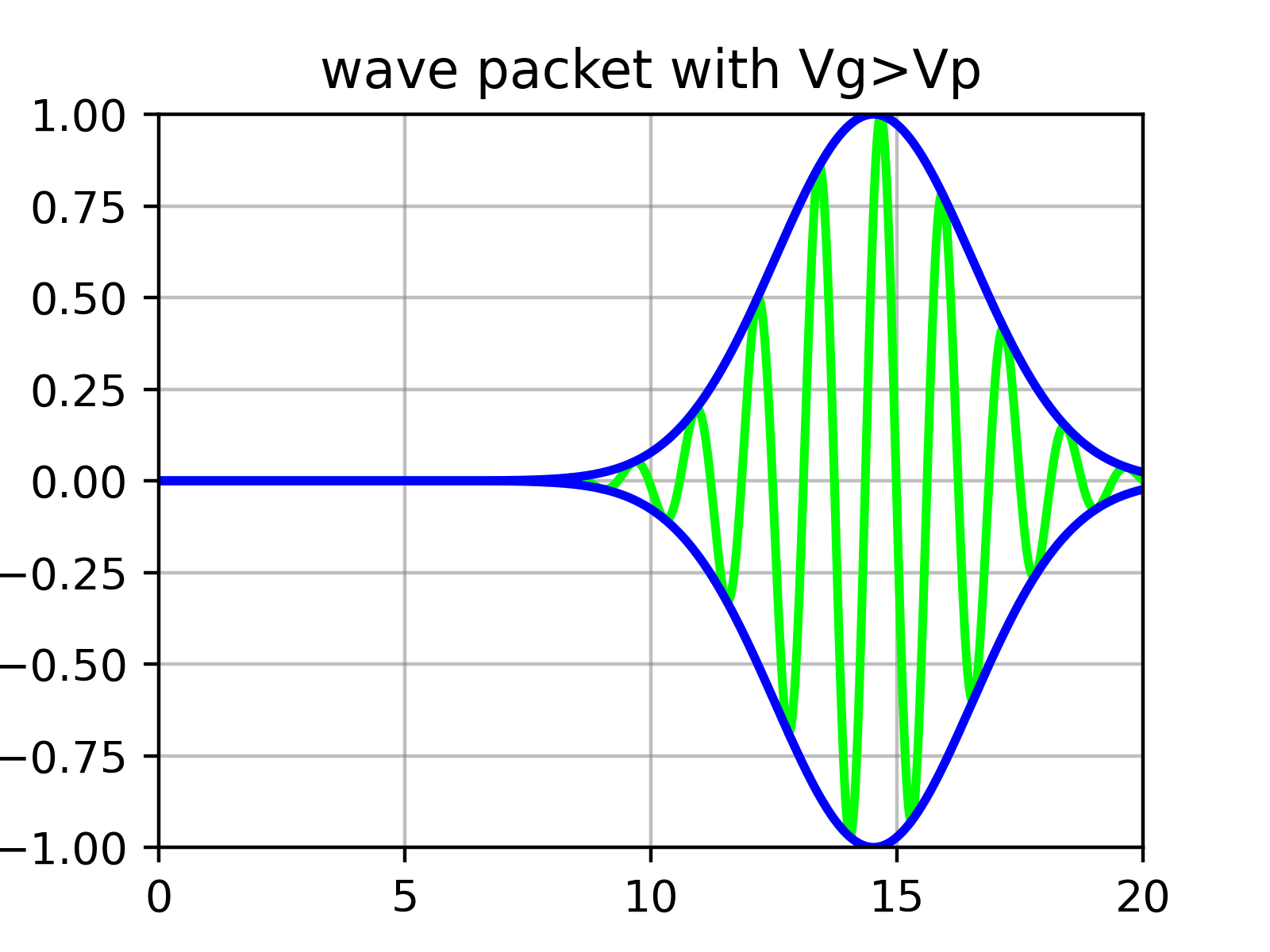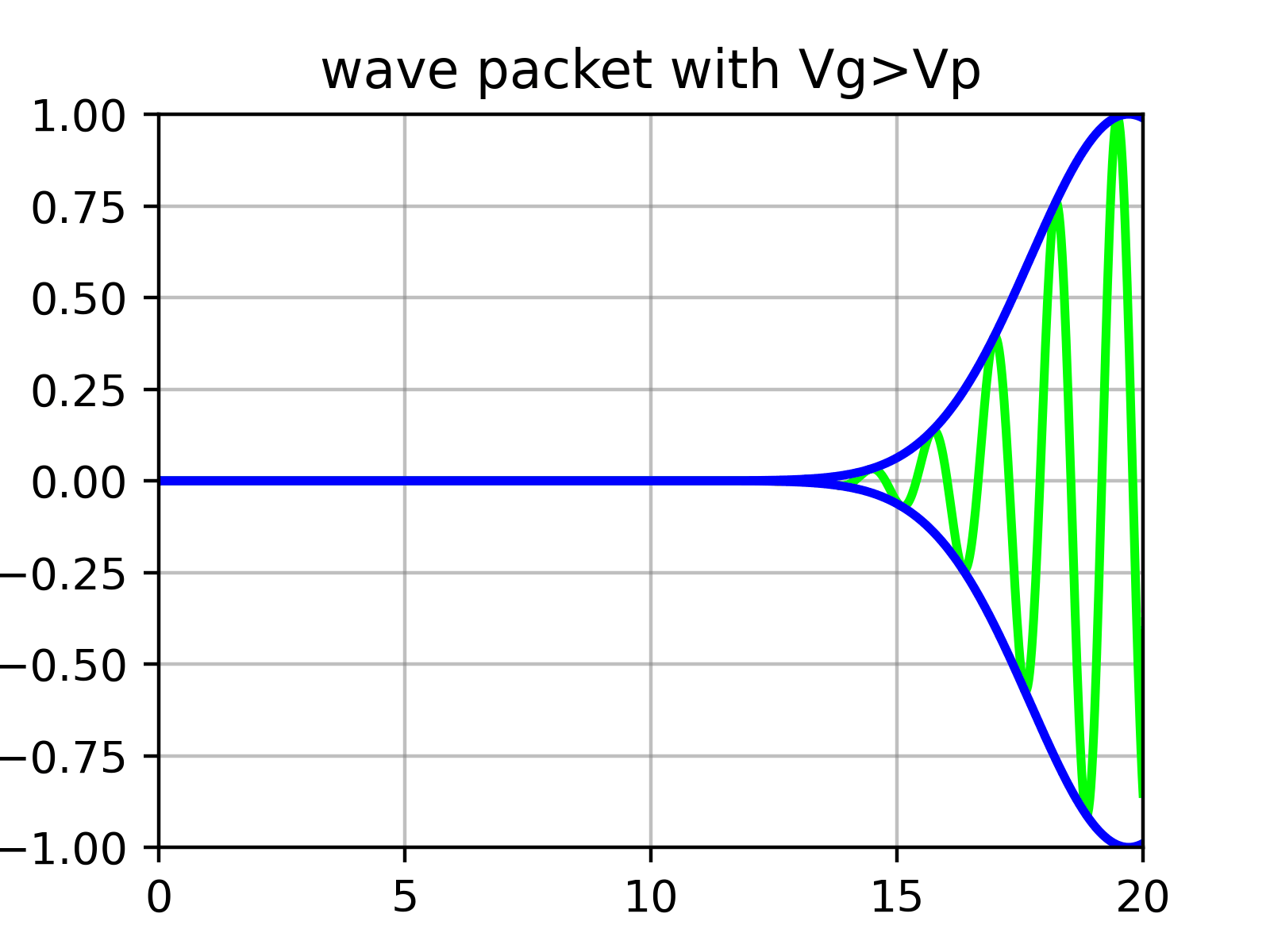
この波動関数は適切な$\phi(k)$に対して規格化できるが、必ず$k$の範囲が必要であり、したがってエネルギーと速度の範囲を持つ。これを波束（wave packet）と呼ぶ。

正弦関数は空間的に無限に広がっているため規格化できない。しかし、このような波動を複数重ね合わせると干渉により局在化され、規格化できる。

プランシュレルの定理（Plancherel theorem）を用いた$\phi(k)$の導出

今、$\Psi(x,t)$の形（式[$\ref{eqn:Psi_general_solution}$]）が分かっているので、初期波動関数

\[\Psi(x,0) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{ikx}dk \label{eqn:Psi_at_t_0}\tag{11}\]

を満たす$\phi(k)$を決定すればよい。これはフーリエ解析（Fourier analysis）の典型的な問題で、プランシュレルの定理（Plancherel’s theorem）で答えを得ることができる。

\[f(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} F(k)e^{ikx}dk \Longleftrightarrow F(k)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(x)e^{-ikx}dx. \label{eqn:plancherel_theorem}\tag{12}\]

$F(k)$を$f(x)$のフーリエ変換（Fourier transform）と呼び、$f(x)$は$F(k)$の逆フーリエ変換（inverse Fourier transform）と呼ぶ。両者の違いは指数の符号のみであることが式($\ref{eqn:plancherel_theorem}$)から容易に確認できる。もちろん積分が存在する関数のみが許可されるという制限条件が存在する。

$f(x)$が存在するための必要十分条件は$\int_{-\infty}^{\infty}|f(x)|^2dx$が有限でなければならないことである。この場合$\int_{-\infty}^{\infty}|F(k)|^2dk$も有限であり、

\[\int_{-\infty}^{\infty}|f(x)|^2 dx = \int_{-\infty}^{\infty}|F(k)|^2 dk\]

である。人によっては式($\ref{eqn:plancherel_theorem}$)ではなく上式をプランシュレルの定理（Plancherel’s theorem）と呼ぶこともある（ウィキペディアでもこのように記述している）。

今の場合、$\Psi(x,0)$が規格化されなければならないという物理的条件により必ず積分が存在する。したがって自由粒子に対する量子力学的解は式($\ref{eqn:Psi_general_solution}$)であり、ここで

\[\phi(k) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\Psi(x,0)e^{-ikx}dx \label{eqn:phi}\tag{13}\]

である。

ただし、実際には式($\ref{eqn:Psi_general_solution}$)の積分を解析的に解ける場合はほとんどない。通常はコンピュータで数値解析を用いて値を求める。

波束の群速度計算および物理的解釈

本質的に波束は$\phi$によって振幅が決定される数多くの正弦関数の重ね合わせである。つまり、波束を構成する「包絡線（envelope）」の中に「さざ波（ripples）」がある。

画像ライセンスおよび原作出典表示

• 画像生成ソースコード（gnuplot）: yunseo-kim/physics-visualizations
• ライセンス: Mozilla Public License 2.0
• 原作者: Ph.D. Youjun Hu
• 原ライセンス表示: MIT License

物理的に粒子の速度に対応するのは、先ほど式($\ref{eqn:phase_velocity}$)で求めた個別のさざ波の速度（位相速度、phase velocity）ではなく、外側の包絡線の速度（群速度、group velocity）である。

位置不確実性と運動量不確実性の関係

式($\ref{eqn:Psi_at_t_0}$)の被積分項$\int\phi(k)e^{ikx}dk$と、式($\ref{eqn:phi}$)の被積分項$\int\Psi(x,0)e^{-ikx}dx$部分のみを取り出して位置不確実性と運動量不確実性の関係を見てみよう。

位置不確実性が小さい場合

位置空間で$\Psi$がある値$x_0$周辺の非常に狭い領域$[x_0-\delta, x_0+\delta]$に分布し、その外の領域では0に近い形の場合（位置不確実性が小さい場合）、$e^{-ikx} \approx e^{-ikx_0}$として$x$に対してほぼ定数であるため

\[\begin{align*} \int_{-\infty}^{\infty} \Psi(x,0)e^{-ikx}dx &\approx \int_{x_0-\delta}^{x_0+\delta} \Psi(x,0)e^{-ikx_0}dx \\ &= e^{-ikx_0}\int_{x_0-\delta}^{x_0+\delta} \Psi(x,0)dx \\ &= e^{-ipx_0/\hbar}\int_{x_0-\delta}^{x_0+\delta} \Psi(x,0)dx \quad (\because \text{式 }\ref{eqn:de_broglie_formula}) \end{align*}\tag{14}\]

である。定積分項は$p$に対して定数であるため、前の$e^{-ipx_0/\hbar}$項により$\phi$は運動量空間で$p$に対する正弦波形を持つようになり、つまり広い運動量区間に分布する（運動量不確実性が大きい）。

運動量不確実性が小さい場合

同様に運動量空間で$\phi$がある値$p_0$周辺の非常に狭い領域$[p_0-\delta, p_0+\delta]$に分布し、その外の領域では0に近い形の場合（運動量不確実性が小さい場合）、式($\ref{eqn:de_broglie_formula}$)により$e^{ikx}=e^{ipx/\hbar} \approx e^{ip_0x/\hbar}$として$p$に対してほぼ定数であり、$dk=\frac{1}{\hbar}dp$であるため

\[\begin{align*} \int_{-\infty}^{\infty} \phi(k)e^{ikx}dk &= \frac{1}{\hbar}\int_{p_0-\delta}^{p_0+\delta} \phi(p)e^{ip_0x/\hbar}dp \\ &= \frac{1}{\hbar}e^{ip_0x/\hbar}\int_{p_0-\delta}^{p_0+\delta} \phi(p)dp \end{align*}\tag{15}\]

である。前の$e^{ip_0x/\hbar}$項により$\Psi$は位置空間で$x$に対する正弦波形を持つようになり、つまり広い位置区間に分布する（位置不確実性が大きい）。

結論

位置不確実性が小さくなると運動量不確実性は大きくなり、逆に運動量不確実性が小さくなると位置不確実性が大きくなる。したがって量子力学的に自由粒子の位置と運動量を同時に正確に知ることは不可能である。

画像出典

• 作者: 英語版ウィキペディアユーザー Maschen
• ライセンス: public domain

実際、不確定性原理（uncertainty principle）により、これは自由粒子だけでなくすべての場合に適用される。不確定性原理は今後別の投稿で扱う予定である。

波束の群速度

式($\ref{eqn:Psi_general_solution}$)の一般解を式($\ref{eqn:phase_velocity}$)と同様に$\omega \equiv \cfrac{\hbar k^2}{2m}$として書き直すと

\[\Psi(x,t) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{i(kx-\omega t)}dk \tag{16}\]

である。

$\omega = \cfrac{\hbar k^2}{2m}$のように$\omega$を$k$に対する関数として表した式を分散関係（dispersion relation）と呼ぶ。後述する内容は分散関係に関係なくすべての波束に対して一般的に適用される。

今、$\phi(k)$が適切な値$k_0$近傍で非常に鋭い形であると仮定しよう。（$k$に対して広く分布しても構わないが、このような波束の形は非常に速く崩れて他の形に変わる。異なる$k$に対する成分はそれぞれ異なる速度で動くため、よく定義された速度を持つ全体の「群」という意味を失う。つまり、運動量の不確実性が大きくなる。）
積分される関数は$k_0$近傍を除いて無視できるため、この点近傍で関数$\omega(k)$をテイラー展開でき、一次項まで書くと

\[\omega(k) \approx \omega_0 + \omega_0^\prime(k-k_0)\]

を得る。今、$s=k-k_0$で置換して$k_0$を中心に積分すると

\[\begin{align*} \Psi(x,t) &= \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\phi(k_0+s)e^{i[(k_0+s)x-(\omega_0+\omega_0^\prime s)t]}ds \\ &= \frac{1}{\sqrt{2\pi}}e^{i(k_0x-\omega_0t)}\int_{-\infty}^{\infty}\phi(k_0+s)e^{is(x-\omega_0^\prime t)}ds. \end{align*}\tag{17}\]

前にある項$e^{i(k_0x-\omega_0t)}$は速度$\omega_0/k_0$で動く正弦波動（「さざ波」）を意味し、この正弦波動の振幅を決定する積分項（「包絡線」）は$e^{is(x-\omega_0^\prime t)}$部分により速度$\omega_0^\prime$で動く。したがって$k=k_0$での位相速度は

\[v_\text{phase} = \frac{\omega_0}{k_0} = \frac{\omega}{k} = \frac{\hbar k}{2m} \tag{18}\]

として式($\ref{eqn:phase_velocity}$)での値と同じであることを再確認でき、群速度は

\[v_\text{group} = \omega_0^\prime = \frac{d\omega}{dk} = \frac{\hbar k}{m} \label{eqn:group_velocity}\tag{19}\]

として位相速度の2倍になる。

古典力学との比較

巨視的スケールで古典力学が成立することを知っているので、量子力学を通じて得た結果は量子論的不確定性が十分小さい場合、古典力学での計算結果に近似できなければならない。今扱っている自由粒子の場合、先ほど仮定したように$\phi(k)$が適切な値$k_0$近傍で非常に鋭い形の場合（つまり、運動量不確実性が十分小さい場合）、量子力学で粒子の速度に対応する群速度$v_\text{group}$が同じ$k$とそれに伴うエネルギー値$E$に対して古典力学で求めた粒子の速度$v_\text{classical}$と等しくなければならない。

先ほど求めた群速度（式[$\ref{eqn:group_velocity}$]）に式($\ref{eqn:t_independent_schrodinger_eqn}$)の$k\equiv \cfrac{\sqrt{2mE}}{\hbar}$を代入すると

\[v_\text{quantum} = \sqrt{\frac{2E}{m}} \tag{20}\]

であり、古典力学で運動エネルギー$E$を持つ自由粒子の速度は同様に

\[v_\text{classical} = \sqrt{\frac{2E}{m}} \tag{21}\]

である。したがって$v_\text{quantum}=v_\text{classical}$であるため、量子力学を適用して得た結果が物理的に妥当な解であることを確認できる。