衝突によるエネルギー伝達

TL;DR

• 衝突時の全エネルギーと運動量は保存される
• すべての電子を失い原子核のみ残ったイオンと電子は運動エネルギーのみを持つ
• 中性原子および一部の電子のみを失ったイオンは内部エネルギーを持ち、ポテンシャルエネルギーの変化に応じて励起(excitation)、脱励起(deexcitation)、またはイオン化(ionization)が起こり得る
• 衝突前後の運動エネルギーの変化による衝突タイプの分類：
  • 弾性衝突(elastic collision)：衝突前後の運動エネルギーの総量が一定
  • 非弾性衝突(inelastic collision)：衝突過程で運動エネルギーが損失する
    • 励起(excitation)
    • イオン化(ionization)
  • 超弾性衝突(superelastic collision)：衝突過程で運動エネルギーが増加する
    • 脱励起(deexcitation)
• 弾性衝突によるエネルギー伝達率：
  • 個別衝突によるエネルギー伝達率：$\zeta_L = \cfrac{4m_1m_2}{(m_1+m_2)^2}\cos^2\theta_2$
  • 衝突当たりの平均エネルギー伝達率：$\overline{\zeta_L} = \cfrac{4m_1m_2}{(m_1+m_2)^2}\overline{\cos^2\theta_2} = \cfrac{2m_1m_2}{(m_1+m_2)^2}$
    • $m_1 \approx m_2$の場合：$\overline{\zeta_L} \approx \cfrac{1}{2}$で、効果的なエネルギー伝達が起こり、速く熱平衡に達する
    • $m_1 \ll m_2$または$m_1 \gg m_2$の場合：$\overline{\zeta_L} \approx 10^{-5}\sim 10^{-4}$で、エネルギー伝達効率が非常に低く、熱平衡に達しにくい。これは弱くイオン化されたプラズマで$T_e \gg T_i \approx T_n$となり、電子温度とイオン温度および中性原子温度が大きく異なる理由である。
• 非弾性衝突によるエネルギー伝達率：
  • 単一衝突による最大内部エネルギー変換率：$\zeta_L = \cfrac{\Delta U_\text{max}}{\cfrac{1}{2}m_1v_1^2} = \cfrac{m_2}{m_1+m_2}\cos^2\theta_2$
  • 平均最大内部エネルギー変換率：$\overline{\zeta_L} = \cfrac{m_2}{m_1+m_2}\overline{\cos^2\theta_2} = \cfrac{m_2}{2(m_1+m_2)}$
    • $m_1 \approx m_2$の場合：$\overline{\zeta_L} \approx \cfrac{1}{4}$
    • $m_1 \gg m_2$の場合：$\overline{\zeta_L} \approx 10^{-5}\sim 10^{-4}$
    • $m_1 \ll m_2$の場合：$\overline{\zeta_L} = \cfrac{1}{2}$で、最も効率的に衝突対象（イオンまたは中性原子）の内部エネルギーを上昇させ、励起状態にできる。これは電子によるイオン化（プラズマ生成）、励起（発光）、分子の解離(dissociation)（ラジカル生成）などがよく起こる理由である。

Prerequisites

• 原子以下の粒子と原子の構成要素

プラズマにおける粒子間衝突

• 衝突時の全エネルギーと運動量は保存される
• すべての電子を失い原子核のみ残ったイオンと電子は運動エネルギーのみを持つ
• 中性原子および一部の電子のみを失ったイオンは内部エネルギーを持ち、ポテンシャルエネルギーの変化に応じて励起(excitation)、脱励起(deexcitation)、またはイオン化(ionization)が起こり得る
• 衝突前後の運動エネルギーの変化による衝突タイプの分類：
  • 弾性衝突(elastic collision)：衝突前後の運動エネルギーの総量が一定
  • 非弾性衝突(inelastic collision)：衝突過程で運動エネルギーが損失する
    • 励起(excitation)
    • イオン化(ionization)
  • 超弾性衝突(superelastic collision)：衝突過程で運動エネルギーが増加する
    • 脱励起(deexcitation)

弾性衝突によるエネルギー伝達

個別衝突によるエネルギー伝達率

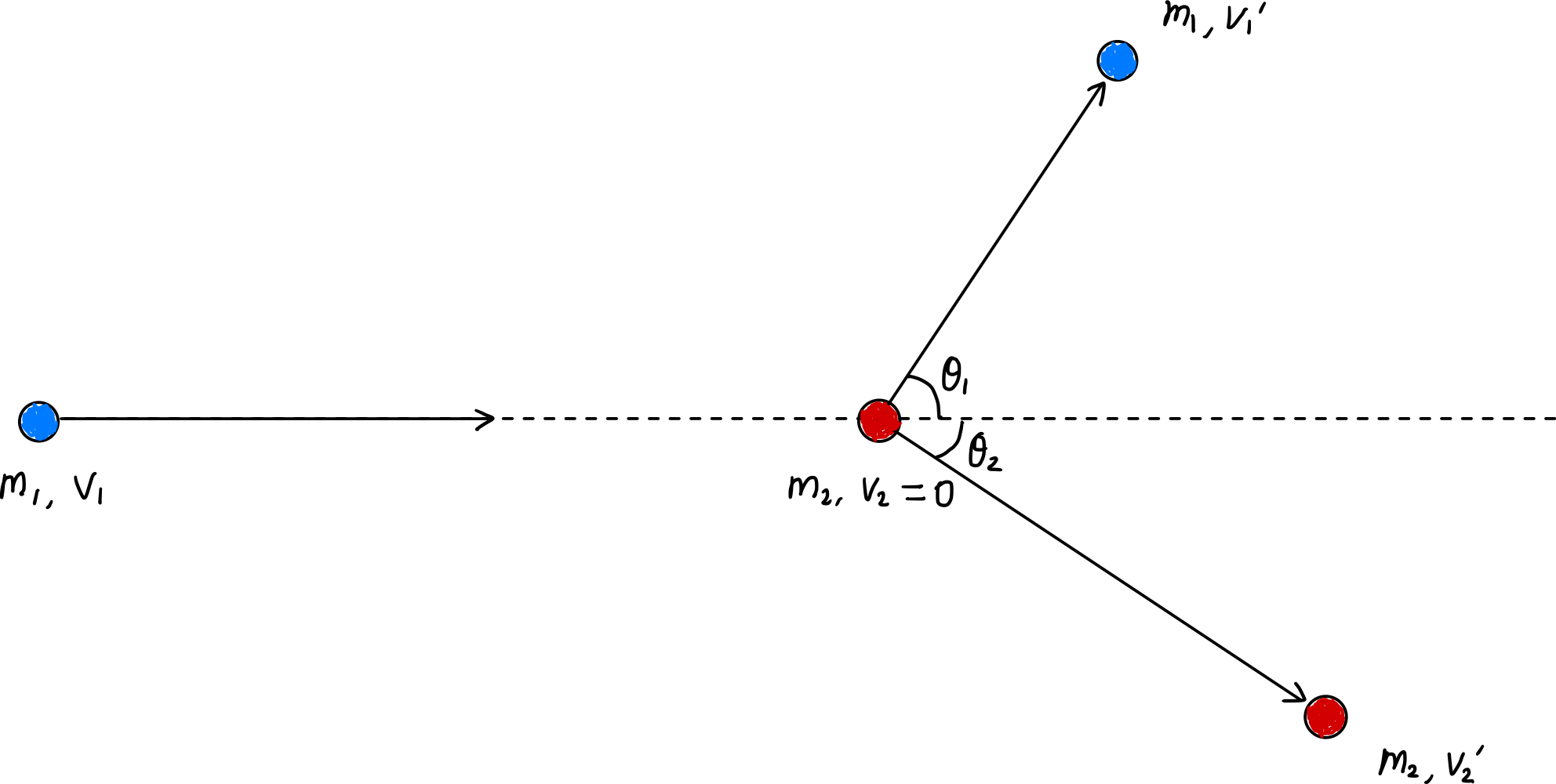
弾性衝突では衝突前後の運動量と運動エネルギーが保存される。

$x$軸と$y$軸についてそれぞれ運動量保存式を立てると

\[\begin{gather*} m_1v_1 = m_1v_1^{\prime}\cos\theta_1 + m_2v_2^{\prime}\cos\theta_2, \label{eqn:momentum_conservation_x}\tag{1} \\ m_1v_1^{\prime}\sin\theta_1 = m_2v_2^{\prime}\sin\theta_2 \label{eqn:momentum_conservation_y}\tag{2} \end{gather*}\]

であり、またエネルギー保存により

\[\frac{1}{2}m_1v_1^2 = \frac{1}{2}m_1{v_1^{\prime}}^2 + \frac{1}{2}m_2{v_2^{\prime}}^2\] \[v_1^2 = {v_1^{\prime}}^2 + \frac{m_2}{m_1}{v_2^{\prime}}^2 \label{eqn:energy_conservation}\tag{3}\]

である。

式（$\ref{eqn:momentum_conservation_x}$）から

\[m_1 v_1^{\prime} \cos \theta_1 = m_1v_1 - m_2v_2^{\prime} \cos \theta_2 \label{eqn:momentum_conservation_x_2}\tag{4}\]

であり、式（$\ref{eqn:momentum_conservation_y}$）と（$\ref{eqn:momentum_conservation_x_2}$）の両辺を二乗して足すと

\[\begin{align*} (m_1v_1^{\prime})^2 &= (m_2 v_2^\prime \sin \theta_2)^2 + (m_1 v_1 - m_2 v_2^\prime \cos \theta_2)^2 \\ &= m_1^2 v_1^2 - 2 m_1 m_2 v_1 v_2^\prime \cos \theta_2 + m_2^2 {v_2^\prime}^2 \tag{5} \end{align*}\]

となる。ここで両辺を$m_1^2$で割ると

\[{v_1^{\prime}}^2 = v_1^2 - 2 \frac{m_2}{m_1} v_1 v_2^\prime \cos \theta_2 + \left(\frac{m_2}{m_1}\right)^2 {v_2^\prime}^2 \label{eqn:momentum_conservation}\tag{6}\]

となる。 ここに式（$\ref{eqn:energy_conservation}$）を代入すると次のように整理できる。

\[\begin{gather*} \left( \frac{m_2}{m_1} \right) {v_2^\prime}^2 = 2 \left( \frac{m_2}{m_1} \right) v_1 v_2^\prime \cos \theta_2 - \left( \frac{m_2}{m_1} \right)^2 {v_2^\prime}^2 \\ 2v_1 \cos \theta_2 = \left(\frac{m_1 + m_2}{m_1} \right) v_2^\prime \\ v_2^{\prime} = \frac{2m_1v_1\cos\theta_2}{m_1 + m_2}. \label{eqn:v_2_prime}\tag{7} \end{gather*}\]

これからエネルギー伝達率$\zeta_L$を次のように得る。

\[\begin{align*} \therefore \zeta_L &= \frac{\cfrac{1}{2}m_2{v_2^\prime}^2}{\cfrac{1}{2}m_1v_1^2} = \frac{m_2}{m_1v_1^2} {\left(\frac{2m_1v_1\cos\theta_2}{m_1 + m_2} \right)}^2 \\ &= \frac{4m_1m_2}{(m_1+m_2)^2}\cos^2\theta_2. \quad \blacksquare \label{eqn:elastic_E_transfer_rate}\tag{8} \end{align*}\]

衝突当たりの平均エネルギー伝達率

$0$から$2\pi$までの角度について$\sin^2{\theta_2}+\cos^2{\theta_2}=1$であり$\overline{\sin^2{\theta_2}}=\overline{\cos^2{\theta_2}}$なので、

\[\begin{align*} \overline{\cos^2{\theta_2}} &= \overline{(1-\sin^2{\theta_2})} = 1 - \overline{\sin^2{\theta_2}} \\ &= 1 - \overline{\cos^2{\theta_2}} \end{align*}\] \[\begin{gather*} 2 \cdot \overline{\cos^2{\theta_2}} = 1 \\ \overline{\cos^2{\theta_2}} = \frac{1}{2}. \end{gather*}\]

これを先ほど求めた式（$\ref{eqn:elastic_E_transfer_rate}$）に代入すると

\[\overline{\zeta_L} = \frac{4m_1m_2}{(m_1+m_2)^2}\overline{\cos^2\theta_2} = \frac{2m_1m_2}{(m_1+m_2)^2}. \quad \blacksquare \label{eqn:elastic_E_mean_transfer_rate}\tag{9}\]

$m_1 \approx m_2$の場合

電子-電子、イオン-イオン、中性原子-中性原子、イオン-中性原子衝突がこれに該当する。このような場合

\[\overline{\zeta_L} = \frac{2m_1m_2}{(m_1+m_2)^2} \approx \frac{1}{2} \label{eqn:elastic_similar_m}\tag{10}\]

となり、効果的なエネルギー伝達が起こり、速く熱平衡に達する。

$m_1 \ll m_2$または$m_1 \gg m_2$の場合

電子-イオン、電子-中性原子、イオン-電子、中性原子-電子衝突がこれに該当する。このような場合は

\[\overline{\zeta_L} = \frac{2m_1m_2}{(m_1+m_2)^2} \approx \frac{2m_1}{m_2}\text{ (}m_1 \ll m_2 \text{の場合を基準)} \approx 10^{-5}\sim 10^{-4} \label{eqn:elastic_different_m}\tag{11}\]

となり、エネルギー伝達効率が非常に低く、熱平衡に達しにくい。これは弱くイオン化されたプラズマで$T_e \gg T_i \approx T_n$となり、電子温度とイオン温度および中性原子温度が大きく異なる理由である。

非弾性衝突によるエネルギー伝達

単一衝突による最大内部エネルギー変換率

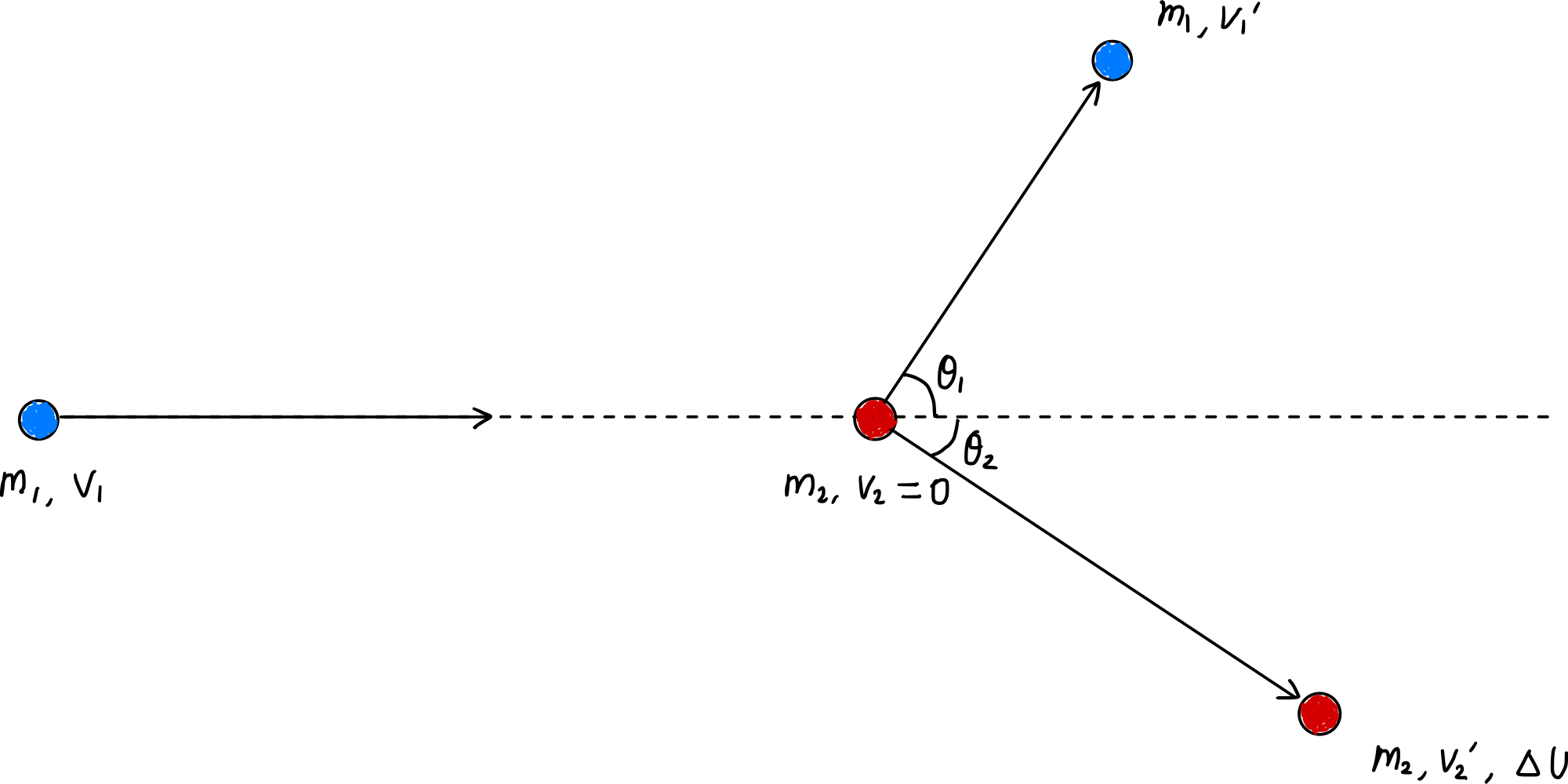
運動量保存（式[$\ref{eqn:momentum_conservation}$]）はこの場合も同様に成り立つが、非弾性衝突なので運動エネルギーは保存されない。このとき非弾性衝突により失われた運動エネルギーは$\Delta U$の内部エネルギーに変換されるので

\[\Delta U = \frac{1}{2} m_1 v_1^2 - \left( \frac{1}{2} m_1 {v_1^{\prime}}^2 + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right) \label{eqn:delta_U}\tag{12}\]

となる。ここに式（$\ref{eqn:momentum_conservation}$）を代入して整理すると次を得る。

\(\begin{align*} \Delta U &= \frac{1}{2} m_1 v_1^2 - \left[ \frac{1}{2} m_1 \left( v_1^2 - 2 \frac{m_2}{m_1} v_1 v_2^{\prime} \cos \theta_2 + \left( \frac{m_2}{m_1} v_2^{\prime} \right)^2 \right) + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right] \\ &= \frac{1}{2} m_1 v_1^2 - \left[ \frac{1}{2} m_1 v_1^2 - m_2 v_1 v_2^{\prime} \cos \theta_2 + \frac{1}{2} \frac{m_2^2}{m_1} {v_2^{\prime}}^2 + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right] \\ &= m_2 v_1 v_2^{\prime} \cos \theta_2 - \frac{1}{2}m_2{v_2^{\prime}}^2\left(\frac{m_1 + m_2}{m_1}\right) \label{eqn:delta_U_2}\tag{13} \end{align*}\).

$\Delta U$を$v_2^\prime$について微分し、その導関数の値が$0$となる極値とその点での最大値を求めると

\[\cfrac{d \Delta U}{d v_2^{\prime}} = m_2 v_1 \cos \theta_2 - m_2 v_2^{\prime} \left( \frac{m_1 + m_2}{m_1} \right) = 0 \tag{14}\] \[\begin{gather*} v_2^{\prime} \left( \frac{m_1 + m_2}{m_1} \right) = v_1 \cos \theta_2 \\ v_2^\prime = \frac{m_1v_1\cos\theta_2}{m_1+m_2}. \end{gather*}\] \[\therefore v_2^{\prime} = \frac{m_1v_1\cos\theta_2}{m_1+m_2} \text{のとき } \Delta U_\text{max} = \frac{1}{2}\frac{m_1m_2 v_1^2 \cos^2\theta_2}{m_1 + m_2}. \label{eqn:delta_U_max}\tag{15}\]

これより、単一非弾性衝突により可能な運動エネルギーから内部エネルギーへの最大変換率$\zeta_L$は次のようになる。

\[\zeta_L = \frac{\Delta U_\text{max}}{\cfrac{1}{2}m_1v_1^2} = \frac{m_2}{m_1+m_2}\cos^2\theta_2. \quad \blacksquare \label{eqn:inelastic_E_transfer_rate}\tag{16}\]

平均最大内部エネルギー変換率

同様に、式（$\ref{eqn:inelastic_E_transfer_rate}$）に$\overline{\cos^2{\theta_2}} = \cfrac{1}{2}$を代入すると次を得る。

\[\overline{\zeta_L} = \frac{m_2}{m_1+m_2}\overline{\cos^2\theta_2} = \frac{m_2}{2(m_1+m_2)}. \label{eqn:inelastic_E_mean_transfer_rate}\tag{17}\]

$m_1 \approx m_2$の場合

イオン-イオン、イオン-中性原子、中性原子-中性原子衝突がこれに該当する。

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} = \frac{1}{4}. \label{eqn:inelastic_similar_m}\tag{18}\]

$m_1 \gg m_2$の場合

イオン-電子、中性原子-電子衝突がこれに該当する。

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} \approx \frac{m_2}{2m_1} \approx 10^{-5}\sim 10^{-4}. \label{eqn:inelastic_ion_electron}\tag{19}\]

$m_1 \ll m_2$の場合

電子-イオン、電子-中性原子衝突がこれに該当する。前の2つの場合は弾性衝突の場合と大きく異なる傾向は見られなかったが、この3番目の場合は重要な違いを示す。この場合

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} \approx \frac{m_2}{2m_2} = \frac{1}{2} \label{eqn:inelastic_electron_ion}\tag{20}\]

となり、最も効率的に衝突対象（イオンまたは中性原子）の内部エネルギーを上昇させ、励起状態にできる。これは後で扱うが、電子によるイオン化（プラズマ生成）、励起（発光）、分子の解離(dissociation)（ラジカル生成）などがよく起こる理由である。