プラズマの定義と温度の概念、そしてサハ方程式(Saha equation)

プラズマの定義における「集団的振る舞い」の意味を考察し、サハ方程式(Saha equation)について学びます。また、プラズマ物理学における温度の概念を明確にします。

Posted Nov 11, 2024 Updated Dec 26, 2024

By Yunseo Kim

views 21 min read

プラズマの定義と温度の概念、そしてサハ方程式(Saha equation)

TL;DR

プラズマ(plasma): 集団的振る舞い(collective behavior)を示す荷電粒子および中性粒子で構成される準中性(quasineutral)気体
プラズマの「集団的振る舞い(collective behavior)」:
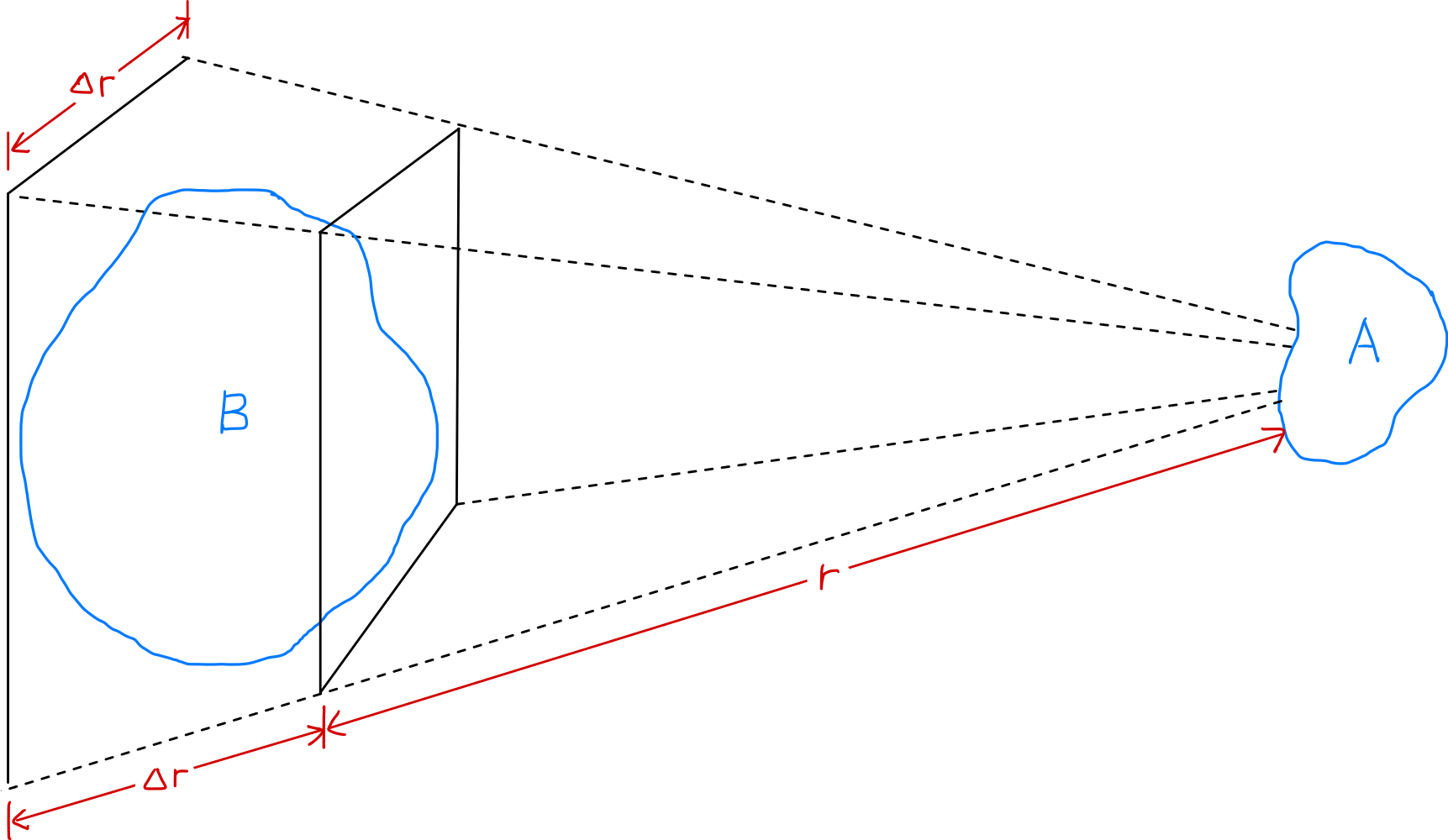
プラズマ内の2つの領域$A$と$B$間の電気力は距離が増加するにつれて$1/r^2$で減少
しかし、与えられた立体角($\Delta r/r$)が一定の場合、$A$に影響を与えうるプラズマ領域$B$の体積は$r^3$で増加
したがって、プラズマを構成する部分は遠距離でも互いに有意な力を及ぼし合うことができる
サハ方程式(Saha equation): 熱平衡状態にある気体のイオン化状態と温度および圧力の関係式
\[\frac{n_{i+1}n_e}{n_i} = \frac{2}{\lambda_{\text{th}}^3}\frac{g_{i+1}}{g_i}\exp{\left[-\frac{\epsilon_{i+1}-\epsilon_i}{k_B T}\right]}\]
プラズマ物理学における温度の概念:
気体とプラズマにおいて粒子あたりの平均運動エネルギーは温度と密接に関連しており、これらは互いに交換可能な物理量である
プラズマ物理学では温度をエネルギーの単位である$\mathrm{eV}$を使用して$kT$の値で表すのが慣例
$1\mathrm{eV}=11600\mathrm{K}$
プラズマは同時に異なる複数の温度を持つことができ、特に電子温度($T_e$)とイオン温度($T_i$)は場合によっては大きく異なる可能性がある
低温プラズマ vs. 高温プラズマ:
プラズマ温度:
低温プラズマ: $T_e \text{(>10,000℃)} \gg T_i \approx T_g \text{(}\sim\text{100℃)}$ $\rightarrow$ 非平衡プラズマ(non-equilibrium plasma)
高温(熱)プラズマ: $T_e \approx T_i \approx T_g \text{(>10,000℃)}$ $\rightarrow$ 平衡プラズマ(equilibrium plasma)
プラズマ密度:
低温プラズマ: $n_g \gg n_i \approx n_e$ $\rightarrow$ イオン化率が小さく、ほとんどが中性粒子として存在
高温(熱)プラズマ: $n_g \approx n_i \approx n_e $ $\rightarrow$ イオン化率が大きい
プラズマの熱容量:
低温プラズマ: 電子温度は高いが密度が低く、ほとんどが比較的低温の中性粒子であるため熱容量が小さく、熱くない
高温(熱)プラズマ: 電子、イオン、中性粒子すべての温度が高いため熱容量が大きく、熱い

Prerequisites

原子以下の粒子と原子の構成要素
マックスウェル-ボルツマン分布(統計力学)
質量とエネルギー、粒子と波動
対称性と保存則(量子力学)、縮退(degeneracy)

プラズマの定義

通常、非専門家向けのプラズマの説明では、プラズマを次のように定義しています。

構成原子が電子と陽イオンに分離してイオン化されるまで気体を加熱して超高温状態にすることで得られる、固体、液体、気体に続く物質の第4の状態

決して間違いではなく、韓国核融合エネルギー研究院(Korea Institute of Fusion Energy)のウェブサイトでもこのように紹介されています。プラズマについて検索すると簡単に見つかる一般的な定義でもあります。

ただし、上記の表現は確かに正しいものの、厳密な定義とは言えません。私たちの周りの常温常圧環境の気体も、極めて小さな割合ではありますが一部がイオン化していますが、だからといってこれをプラズマとは呼びません。塩化ナトリウムのようなイオン結合物質を水に溶かすと電荷を帯びたイオンに分離しますが、このような溶液もプラズマではありません。
つまり、プラズマが物質のイオン化された状態であることは正しいですが、イオン化されたからといってすべてがプラズマというわけではありません。

より厳密に、プラズマは次のように定義できます。

プラズマは集団的振る舞いを示す荷電粒子および中性粒子で構成される準中性気体である。
A plasma is a quasineutral gas of charged and neutral particles which exhibits collective behavior.
by Fransis F. Chen

「準中性(quasineutrality)」が何を意味するかは、後ほどデバイ遮蔽(Debye shielding)を扱う際に見ていきます。ここでは、プラズマの「集団的振る舞い(collective behavior)」がどのような意味を持つのかを見ていきましょう。

プラズマの集団的振る舞い

中性粒子で構成される非イオン化気体の場合、各気体分子は電気的に中性であるため、作用する正味の電磁力は$0$であり、重力の影響も無視できます。分子は他の分子と衝突するまでは妨げられることなく動き、分子間の衝突が粒子の運動を決定します。たとえ一部の粒子がイオン化して電荷を帯びたとしても、全体の気体中でイオン化された粒子の割合が非常に低いため、これらの荷電粒子の電気的影響力は距離に応じて$1/r^2$で減衰し、遠くまで及びません。

しかし、荷電粒子を多数含むプラズマでは状況が全く異なります。荷電粒子の移動によって正電荷または負電荷の局所的な集中が発生する可能性があり、これにより電場が生じます。また、電荷の移動は電流を作り、電流は磁場を作ります。このような電場と磁場は、粒子間の衝突がなくても遠く離れた他の粒子にまで影響を及ぼすことができます。

わずかに電荷を帯びた2つのプラズマ領域$A$と$B$の間に作用する電気力の強さが距離$r$に応じてどのように変化するかを見てみましょう。$A$と$B$の間のクーロンの法則に従う電気力(Coulomb force)は距離が増加するにつれて$1/r^2$で減少します。しかし、与えられた立体角($\Delta r/r$)が一定の場合、$A$に影響を与えうるプラズマ領域$B$の体積は$r^3$で増加します。したがって、プラズマを構成する部分は遠距離でも互いに有意な力を及ぼし合うことができます。このように遠距離まで作用する電気力は、プラズマが非常に多様な運動パターンを示すことを可能にし、プラズマ物理学(plasma physics)という独立した学問分野が存在する理由でもあります。「集団的振る舞い(collective behavior)」とは、このようにある領域の運動がその領域での局所的な条件だけでなく、遠く離れた他の領域のプラズマ状態にも影響を受けることを意味します。

サハ方程式 (Saha equation)

サハ方程式(Saha equation)は熱平衡状態にある気体のイオン化状態と温度および圧力の関係式で、インドの天体物理学者メグナド・サハ(Meghnad Saha)が考案しました。

\[\frac{n_{i+1}n_e}{n_i} = \frac{2}{\lambda_{\text{th}}^3}\frac{g_{i+1}}{g_i}\exp{\left[-\frac{\epsilon_{i+1}-\epsilon_i}{k_B T}\right]} \label{eqn:saha_eqn}\tag{1}\]

$n_i$: $i$価陽イオン($i$個の電子を失った陽イオン)の密度
$g_i$: $i$価陽イオンの状態縮退度(degeneracy)
$\epsilon_i$: 中性原子から$i$個の電子を取り除いて$i$価陽イオンを作るのに必要なエネルギー
- $\epsilon_{i+1}-\epsilon_i$: $(i+1)$次イオン化エネルギー
$n_e$: 電子密度
$k_B$: ボルツマン定数
$\lambda_{\text{th}}$: 熱的ド・ブロイ波長(与えられた温度での気体中の電子の平均ド・ブロイ波長)

\[\lambda_{\text{th}} \equiv \frac{h}{\sqrt{2\pi m_e k_B T}} \quad \text{ (}h\text{: プランク定数)} \label{eqn:lambda_th}\tag{2}\]

$m_e$: 電子質量
$T$: 気体の温度

もし1段階のイオン化のみが重要で、2価以上の陽イオンの生成が無視できる場合であれば、$n_1=n_i=n_e$、$n_0=n_n$、$U_i = \epsilon = \epsilon_1$、$i=0$とおいて次のように単純化できます。

\[\begin{align*} \frac{n_i^2}{n_n} &= \frac{2}{\lambda_{th}^3}\frac{g_1}{g_0}\exp{\left[-\frac{\epsilon}{k_B T} \right]} \label{eqn:saha_eqn_approx}\tag{3}\\ &= 2\left(\frac{2\pi m_e k_B T}{h^2}\right)^{3/2}\frac{g_1}{g_0}e^{-U_i/{k_B T}} \\ &= 2\frac{g_1}{g_0}\left(\frac{2\pi m_e k_B}{h^2}\right)^{3/2}T^{3/2}e^{-U_i/{k_B T}}. \label{eqn:saha_eqn_approx_2}\tag{4} \end{align*}\]

常温常圧環境での空気(窒素)のイオン化率

上式で$2 \cfrac{g_1}{g_0}$の値は気体の成分ごとに異なりますが、多くの場合、この値のオーダー(order of magnitude)は$1$です。したがって、おおよそ次のように近似できます。

\[\frac{n_i^2}{n_n} \approx \left(\frac{2\pi m_e k_B}{h^2}\right)^{3/2} T^{3/2} e^{-U_i/{k_B T}}.\]

SI単位系での基本定数$m_e$、$k_B$、$h$の値はそれぞれ

$m_e \approx 9.11 \times 10^{-31} \mathrm{kg}$
$k_B \approx 1.38 \times 10^{-23} \mathrm{J/K}$
$h \approx 6.63 \times 10^{-34} \mathrm{J \cdot s}$

であり、これを上式に代入すると次を得ます。

\[\frac{n_i^2}{n_n} \approx 2.4 \times 10^{21}\ T^{3/2} e^{-U_i/{k_B T}}. \label{eqn:fractional_ionization}\tag{5}\]

これより、常温常圧環境($n_n \approx 3 \times 10^{25} \mathrm{m^{-3}}$、$T\approx 300\mathrm{K}$)の窒素($U_i \approx 14.5\mathrm{eV} \approx 2.32 \times 10^{-18}\mathrm{J}$)についてイオン化率$n_i/(n_n + n_i) \approx n_i/n_n$の近似値を計算すると

\[\frac{n_i}{n_n} \approx 10^{-122}\]

と極めて低い割合であることがわかります。これが宇宙環境とは異なり、地表面や海面付近の大気環境では自然にはプラズマにほとんど遭遇できない理由です。

プラズマ物理学における温度の概念

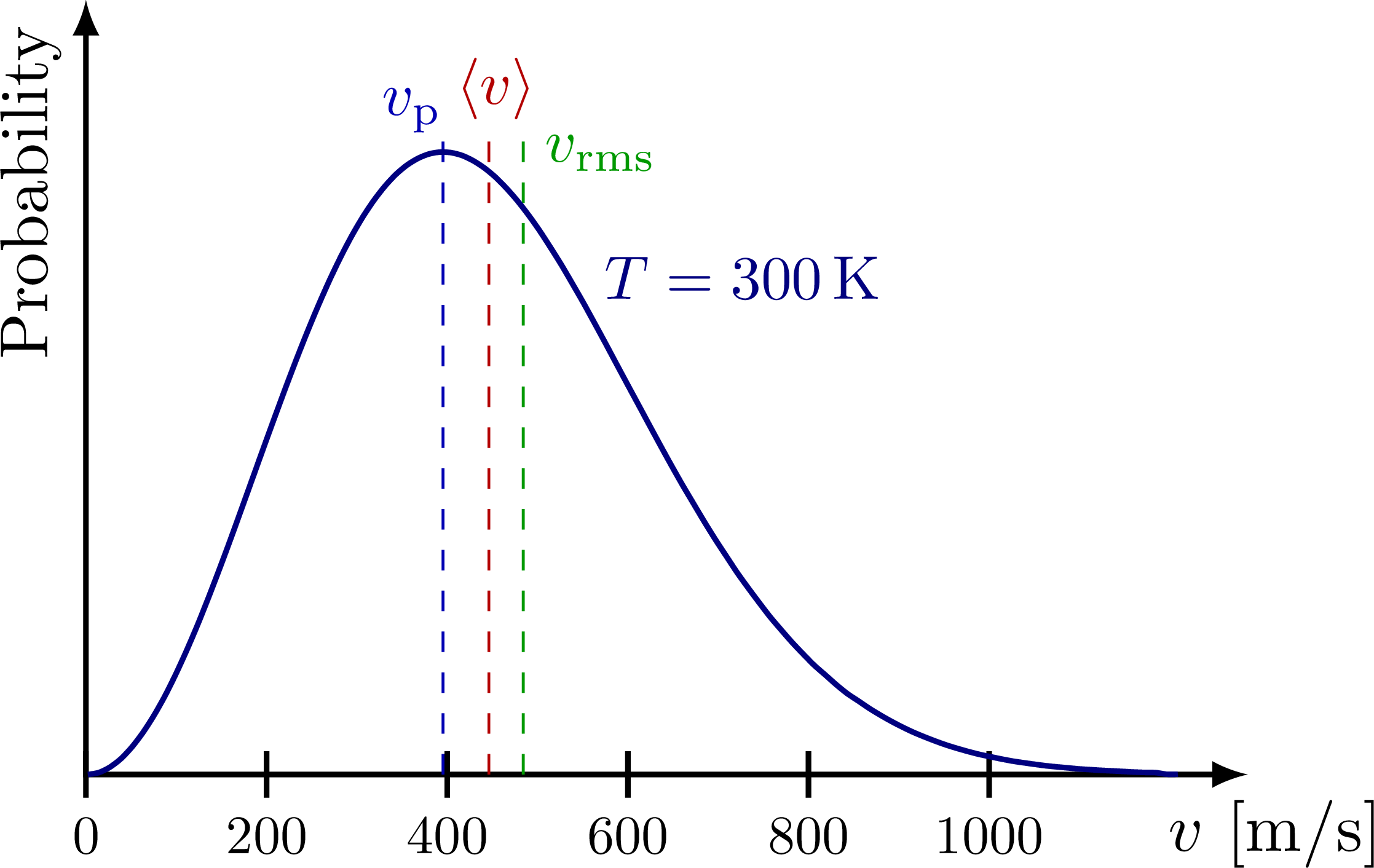
熱平衡状態の気体を構成する粒子の速度は、概ね次のようなマックスウェル-ボルツマン分布(Maxwell–Boltzmann distribution)に従います。

\[f(v) = \left(\frac{m}{2\pi k_B T} \right)^{3/2} 4\pi v^2 \exp{\left(-\frac{mv^2}{2k_B T} \right)} \label{eqn:maxwell_boltzmann_dist}\tag{6}\]

画像出典
作者: TikZ.net author Izaak Neutelings
ライセンス: CC BY-SA 4.0

最頻速度(most probable speed): $v_p = \sqrt{\cfrac{2k_B T}{m}}$
平均速度(mean speed): $\langle v \rangle = \sqrt{\cfrac{8k_B T}{\pi m}}$
二乗平均平方根速度(RMS speed): $v_{rms} = \sqrt{\langle v^2 \rangle} = \sqrt{\cfrac{3k_B T}{m}}$

温度$T$での粒子1個あたりの平均運動エネルギーは$\cfrac{1}{2}m\langle v^2 \rangle = \cfrac{1}{2}mv_{rms}^2 = \cfrac{3}{2}k_B T$(自由度$3$基準)で温度のみによって決定されます。このように気体とプラズマにおいて粒子あたりの平均運動エネルギーは温度と密接に関連しており、これらは互いに交換可能な物理量であるため、プラズマ物理学では温度をエネルギーの単位である$\mathrm{eV}$で表すのが慣例です。次元数の混乱を避けるため、平均運動エネルギー$\langle E_k \rangle$の代わりに$kT$の値で温度を表します。

$kT=1\mathrm{eV}$のときの温度$T$は

\[\begin{align*} T\mathrm{[K]} &= \frac{1.6 \times 10^{-19}\mathrm{[J]}}{1.38 \times 10^{-23}\mathrm{[J/K]}} \\ &= 11600\mathrm{[K]} \end{align*} \label{eqn:temp_conv_factor}\tag{7}\]

であるため、プラズマ物理学で温度を表す場合、$1\mathrm{eV}=11600\mathrm{K}$を意味します。
例) 温度が$2\mathrm{eV}$のプラズマの$kT$値は$2\mathrm{eV}$であり、粒子あたりの平均運動エネルギーは$\cfrac{3}{2}kT=3\mathrm{eV}$です。

またプラズマは同時に複数の温度を持つことができます。プラズマではイオン同士の衝突または電子同士の衝突の頻度が電子とイオンの間の衝突頻度よりも大きく、このため電子とイオンはそれぞれ異なる温度(電子温度$T_e$とイオン温度$T_i$)で熱平衡に達して別々のマックスウェル-ボルツマン分布を形成することができ、場合によっては電子温度とイオン温度が大きく異なる可能性があります。さらに、外部から磁場$\vec{B}$が加えられる場合、同じ種類の粒子(例えばイオン)でも運動の方向が磁場に平行か垂直かによって受けるローレンツ力(Lorentz force)の大きさが異なるため、互いに異なる温度$T_\perp$と$T_\parallel$を持つことができます。

温度、圧力と密度の関係

理想気体の法則によると

\[PV = \left(\frac{N}{N_A}\right)RT = NkT \label{eqn:ideal_gas_law}\tag{8}\]

であり、これより

\[\begin{gather*} P = \frac{NkT}{V} = nkT, \\ n = \frac{P}{kT} \end{gather*} \label{eqn:relation_between_T_P_n}\tag{9}\]

となります。つまり、プラズマの密度は温度($kT$)に反比例し、圧力($P$)に比例します。

プラズマの分類: 低温プラズマ vs. 高温プラズマ

Low-temperature non-thermal cold plasma	Low-temperature thermal cold plasma	High-temperature hot plasma
$T_i \approx T \approx 300 \mathrm{K}$ $T_i \ll T_e \leqslant 10^5 \mathrm{K}$	$T_i \approx T_e \approx T < 2 \times 10^4 \mathrm{K}$	$T_i \approx T_e > 10^6 \mathrm{K}$
Low pressure($\sim 100\mathrm{Pa}$) glow and arc	Arcs at $100\mathrm{kPa}$ ($1\mathrm{atm}$)	Kinetic plasma, fusion plasma

プラズマ温度

電子温度を$T_e$、イオン温度を$T_i$、中性粒子温度を$T_g$とすると、

低温プラズマ: $T_e \mathrm{(>10,000 K)} \gg T_i \approx T_g \mathrm{(\sim 100 K)}$ $\rightarrow$ 非平衡プラズマ(non-equilibrium plasma)
高温(熱)プラズマ: $T_e \approx T_i \approx T_g \mathrm{(>10,000 K)}$ $\rightarrow$ 平衡プラズマ(equilibrium plasma)

となります。

プラズマ密度

電子密度を$n_e$、イオン密度を$n_i$、中性粒子密度を$n_g$とすると、

低温プラズマ: $n_g \gg n_i \approx n_e$ $\rightarrow$ イオン化率が小さく、ほとんどが中性粒子として存在
高温(熱)プラズマ: $n_g \approx n_i \approx n_e $ $\rightarrow$ イオン化率が大きい