連続X線と特性X線(Continuous and Characteristic X Rays)

TL;DR

• bremsstrahlung(制動放射、breaking radiation): 電子などの荷電粒子が原子核付近を通過する際、電気的引力により加速されながら放出する連続スペクトルのX線
• 最小波長: $\lambda_\text{min} = \cfrac{hc}{E_\text{max}} = \cfrac{12400 \text{[Å}\cdot\text{eV]}}{V\text{[eV]}}$
• 特性X線(characteristic X-ray): 入射電子が内側の電子殻の電子と衝突して原子をイオン化させた際、外側電子殻にあった他の電子が内側の空位に遷移する際に放出される、二つのエネルギー準位間の差に相当するエネルギーを持つ不連続なスペクトルのX線

Prerequisites

• 原子以下の粒子と原子の構成要素

X線の発見

レントゲン(Röntgen)は電子ビームを標的に照射した際にX線が発生することを発見した。発見当時はX線が電磁波であることが分からなかったため、正体不明という意味でX線(X-ray)と名付けられ、また発見者の名前にちなんでレントゲン線(Röntgen radiation)とも呼ばれる。

上の画像は典型的なX線管(X-ray tube)の構造を簡単に示したものである。X線管内部にはタングステンフィラメントで構成された陰極と標的が固定された陽極が真空状態で密封されている。陽極間に数十kVの高電圧をかけると陰極から電子が放出され陽極の標的に照射され、これによりX線が放出される。ただしこの時X線へのエネルギー変換効率は通常1%以下と非常に低く、残りの99%以上のエネルギーは熱に変換されるため、冷却のための別途の装置が追加で必要となる。

bremsstrahlung (制動放射、braking radiation)

電子などの荷電粒子が原子核付近を通過する際、その粒子と原子核の間に働く電気的引力により急激に進行経路が曲がり、また減速しながらX線の形でエネルギーを放出する。このプロセスでのエネルギー変換は量子化されていないため、放出されるX線は連続スペクトルを示し、これをbremsstrahlungまたは制動放射(braking radiation)という。

ただし、bremsstrahlungにより放出されるX線の光子が持つエネルギーは当然入射した電子の運動エネルギーを超えることはできない。したがって放出されるX線の最小波長が存在し、これは次の式で簡単に求めることができる。

\[\lambda_\text{min} = \frac{hc}{E}. \tag{1}\]

プランク定数$h$と光速$c$は定数であるため、この最小波長は入射する電子のエネルギーによってのみ決定される。$1\text{eV}$のエネルギーに対応する波長$\lambda$は約$1.24 \mu\text{m}=12400\text{Å}$である。したがってX線管に$V$ボルトの電圧をかけた時の最小波長$\lambda_\text{min}$は次のようになる。実質的にはこの公式が多く使用される。

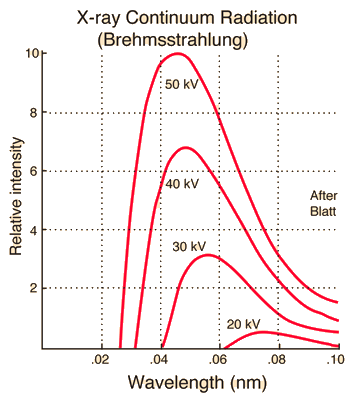
\[\lambda_\text{min} \text{[Å]} = \frac{12400 \text{[Å}\cdot\text{eV]}}{V\text{[eV]}}. \label{eqn:lambda_min}\tag{2}\]

次のグラフはX線管に流れる電流量を一定に保ちながら電圧を変えた時の連続X線スペクトルを示したものである。電圧が高くなるほど最小波長$\lambda_{\text{min}}$が短くなり、全体的なX線の強度が増加することが確認できる。

特性X線 (characteristic X-ray)

もしX線管にかける電圧が十分に大きければ、入射電子が標的原子の内側電子殻にある電子と衝突して該当原子をイオン化させることができる。この場合、外側電子殻の電子が急速にエネルギーを放出しながらその内側電子殻の空位を埋めるが、その過程で二つのエネルギー準位の差に等しいエネルギーを持つX線光子が発生する。このプロセスで放出されるX線のスペクトルは不連続であり、標的原子の固有のエネルギー準位により決定され、入射する電子ビームのエネルギーや強度とは無関係である。これを特性X線(characteristic X-ray)という。

Siegbahn notation

画像出典

• 作者: 英語版ウィキペディアユーザー HenrikMidtiby
• ライセンス: CC BY-SA 3.0

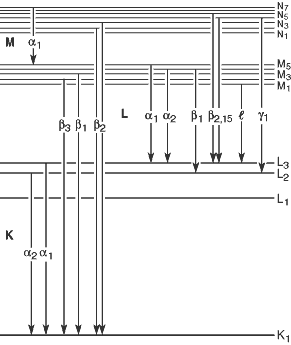
Siegbahn表記法によると、K殻の空位をL殻、M殻、…の電子が埋める時に放出されるX線を上の画像のように$K_\alpha$、$K_\beta$、…と呼ぶ。ただしSiegbahn表記法の後に現代原子モデルが登場し、多電子原子の場合、ボーア原子モデルの各殻（同じ主量子数を持つエネルギー準位）内でも他の量子数によってエネルギー準位が異なることが分かったことにより、各$K_\alpha$、$K_\beta$、…についても再び$K_{\alpha_1}$、$K_{\alpha_2}$、…のような細分類を設けることになった。

このような伝統的な表記法は現在でも分光学分野で広く使用されている。しかし名称が体系的でなく、しばしば混乱を引き起こすという問題点があるため、国際純正・応用化学連合(IUPAC)では以下のような異なる表記法を使用することを推奨している。

IUPAC notation

IUPACが推奨する原子軌道および特性X線の標準表記法は次の通りである。 まず、それぞれの原子軌道に以下の表のように名前を割り当てる。

$n$(主量子数)	$l$(方位量子数)	$s$(スピン量子数)	$j$(角運動量量子数)	原子軌道	X線表記
$1$	$0$	$\pm1/2$	$1/2$	$1s_{1/2}$	$K_{(1)}$
$2$	$0$	$\pm1/2$	$1/2$	$2s_{1/2}$	$L_1$
$2$	$1$	$-1/2$	$1/2$	$2p_{1/2}$	$L_2$
$2$	$1$	$+1/2$	$3/2$	$2p_{3/2}$	$L_3$
$3$	$0$	$\pm1/2$	$1/2$	$3s_{1/2}$	$M_1$
$3$	$1$	$-1/2$	$1/2$	$3p_{1/2}$	$M_2$
$3$	$1$	$+1/2$	$3/2$	$3p_{3/2}$	$M_3$
$3$	$2$	$-1/2$	$3/2$	$3d_{3/2}$	$M_4$
$3$	$2$	$+1/2$	$5/2$	$3d_{5/2}$	$M_5$
$4$	$0$	$\pm1/2$	$1/2$	$4s_{1/2}$	$N_1$
$4$	$1$	$-1/2$	$1/2$	$4p_{1/2}$	$N_2$
$4$	$1$	$+1/2$	$3/2$	$4p_{3/2}$	$N_3$
$4$	$2$	$-1/2$	$3/2$	$4d_{3/2}$	$N_4$
$4$	$2$	$+1/2$	$5/2$	$4d_{5/2}$	$N_5$
$4$	$3$	$-1/2$	$5/2$	$4f_{5/2}$	$N_6$
$4$	$3$	$+1/2$	$7/2$	$4f_{7/2}$	$N_7$

全角運動量量子数 $j=|l+s|$.

そして原子を構成する電子がある一つのエネルギー準位からそれより低いエネルギー準位に遷移する際に放出する特性X線を次のルールに従って呼ぶ。

\[\text{(遷移後のエネルギー準位のX線表記)-(遷移前のエネルギー準位のX線表記)}\]

例えば、$2p_{1/2}$軌道の電子が$1s_{1/2}$に遷移する際に放出される特性X線は$\text{K-L}_2$と呼ぶことができる。

X線スペクトル

上はロジウム(Rh)標的に60kVで加速された電子ビームを照射した際に放出されるX線スペクトルである。bremsstrahlungによる滑らかで連続的な形状の曲線が現れ、式($\ref{eqn:lambda_min}$)に従って約$0.207\text{Å} = 20.7\text{pm}$以上の波長についてのみX線が放出されることが確認できる。また、グラフの中間中間に現れる鋭いピークはロジウム原子固有のK殻X線によるものである。前述したように標的原子の種類によって固有の特性X線スペクトルを持つため、ある標的に電子ビームを照射して出てくるX線スペクトルでスパイクが観察される波長を調べることで、その標的の構成元素を特定することができる。

$K_\alpha、K_\beta、\dots$だけでなく$L_\alpha、L_\beta、\dots$のようなより低いエネルギーのX線ももちろん放出される。しかしこれらはずっと低いエネルギーを持ち、大抵X線管のハウジング(housing)で吸収されて検出器まで到達しない。