調和振動子(The Harmonic Oscillator)の解析的解法
量子力学における調和振動子のシュレーディンガー方程式を立て、その方程式の解析的な解法を学ぶ。 無次元変数ξを導入して方程式を解き、任意の規格化された定常状態をエルミート多項式を用いて表す。
TL;DR
\[\begin{gather*} \psi(\xi) = h(\xi)e^{-\xi^2/2} \quad \text{(ただし、}\lim_{\xi\to\infty}h(\xi)=A\text{)}, \\ \frac{d^2h}{d\xi^2}-2\xi\frac{dh}{d\xi}+(K-1)h = 0 \end{gather*}\]
- 振幅が十分に小さければ、どのような振動も単純調和振動(simple harmonic oscillation)で近似でき、これにより単純調和振動は物理学で重要な意味を持つ
- 調和振動子:$V(x) = \cfrac{1}{2}kx^2 = \cfrac{1}{2}m\omega^2 x^2$
- 無次元変数$\xi$と$\cfrac{1}{2}\hbar\omega$単位で表したエネルギー$K$を導入:
- $\xi \equiv \sqrt{\cfrac{m\omega}{\hbar}}x$
- $K \equiv \cfrac{2E}{\hbar\omega}$
- $ \cfrac{d^2\psi}{d\xi^2} = \left(\xi^2-K \right)\psi $
- $|\xi|^2 \to \infty$のとき、物理的に許容される漸近解は$\psi(\xi) \to Ae^{-\xi^2/2}$なので、
\[a_{j+2} = \frac{(2j+1-K)}{(j+1)(j+2)}a_j\]
- 上記方程式の解を級数形式$ h(\xi) = a_0 + a_1\xi + a_2\xi^2 + \cdots = \sum_{j=0}^{\infty}a_j\xi^j$で表すと、
\[h_n(\xi) = \begin{cases} a_0 H_n(\xi), & n=2k & (k=0,1,2,\dots) \\ a_1 H_n(\xi), & n=2k+1 & (k=0,1,2,\dots) \end{cases}\]
- この解が規格化されるためには、級数$\sum a_j$は有限でなければならず、つまりある「最大の」$j$値$n\in \mathbb{N}$が存在し、$j>n$のとき$a_j=0$でなければならないので、
- $ K = 2n + 1 $
- $ E_n = \left(n+\cfrac{1}{2} \right)\hbar\omega, \quad n=0,1,2,\dots $
- 一般的に$h_n(\xi)$は$\xi$の$n$次多項式であり、ここで前の係数($a_0$または$a_1$)を除いた残りをエルミート多項式(Hermite polynomials) $H_n(\xi)$と呼ぶ
\[\psi_n(x) = \left(\frac{m\omega}{\pi\hbar} \right)^{1/4} \frac{1}{\sqrt{2^n n!}}H_n(\xi)e^{-\xi^2/2}\]
- 調和振動子の規格化された定常状態:
- 量子振動子の特徴
- 固有関数として偶関数と奇関数が交互に現れる
- 古典力学的には存在し得ない領域(与えられた$E$に対する古典的な振幅より大きな$x$)でも発見される確率が$0$ではなく、低い確率ではあるが粒子が存在し得る
- $n$が奇数のすべての定常状態に対して、中心で粒子を発見する確率は$0$
- $n$が大きいほど古典的振動子に類似する
Prerequisites
モデルの設定
古典力学における調和振動子の記述方法と、調和振動子問題が持つ重要性については前回の記事を参照してください。
量子力学における調和振動子
量子力学的調和振動子問題は、ポテンシャル
\[V(x) = \frac{1}{2}m\omega^2 x^2 \label{eqn: potential_omega}\tag{1}\]に対するシュレーディンガー方程式を解くことです。調和振動子に対する時間に依存しないシュレーディンガー方程式は
\[-\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2} + \frac{1}{2}m\omega^2x^2\psi = E\psi \label{eqn:t_independent_schrodinger_eqn}\tag{2}\]です。
この問題を解くには、全く異なる二つのアプローチがあります。一つはべき級数(power series)を用いた解析的な方法(analytic method)で、もう一つははしご演算子(ladder operators)を用いた代数的な方法(algebraic method)です。代数的な方法の方が速くて簡単ですが、べき級数を用いた解析的な解法も学ぶ必要があります。以前に代数的な解法を扱いましたが、ここでは解析的な解法を扱います。
シュレーディンガー方程式の変形
無次元の変数
\[\xi \equiv \sqrt{\frac{m\omega}{\hbar}}x \label{eqn:xi}\tag{3}\]を導入すると、時間に依存しないシュレーディンガー方程式($\ref{eqn:t_independent_schrodinger_eqn}$)を次のように簡単に書くことができます。
\[\frac{d^2\psi}{d\xi^2} = \left(\xi^2-K \right)\psi. \label{eqn:schrodinger_eqn_with_xi}\tag{4}\]ここで$K$は$\cfrac{1}{2}\hbar\omega$単位で表したエネルギーです。
\[K \equiv \frac{2E}{\hbar\omega}. \label{eqn:K}\tag{5}\]これで書き直した方程式($\ref{eqn:schrodinger_eqn_with_xi}$)を解けばよいです。まず、非常に大きな$\xi$に対して(つまり非常に大きな$x$に対して)$\xi^2 \gg K$なので、
\[\frac{d^2\psi}{d\xi^2} \approx \xi^2\psi \label{eqn:schrodinger_eqn_approx}\tag{6}\]となり、これに対する近似的な解は
\[\psi(\xi) \approx Ae^{-\xi^2/2} + Be^{\xi^2/2} \label{eqn:psi_approx}\tag{7}\]です。しかし、ここで$B$項は$|x|\to \infty$のとき発散して規格化できないため、物理的に許容される漸近解は
\[\psi(\xi) \to Ae^{-\xi^2/2} \label{eqn:psi_asymp}\tag{8}\]です。ここで指数部分を分離して
\[\psi(\xi) = h(\xi)e^{-\xi^2/2} \quad \text{(ただし、}\lim_{\xi\to\infty}h(\xi)=A\text{)} \label{eqn:psi_and_h}\tag{9}\]と書きましょう。
指数項$e^{-\xi^2/2}$を見出すために、導出過程で近似法を用いて漸近解の形を見つけただけで、これによって得られた式($\ref{eqn:psi_and_h}$)は近似的な式ではなく正確な式です。このように漸近形を分離することは、微分方程式をべき級数形式で解く際に使用する標準的な最初のステップです。
式($\ref{eqn:psi_and_h}$)を微分して$\cfrac{d\psi}{d\xi}$と$\cfrac{d^2\psi}{d\xi^2}$を求めると
\[\begin{gather*} \frac{d\psi}{d\xi} = \left(\frac{dh}{d\xi}-\xi h \right)e^{-\xi^2/2}, \\ \frac{d^2\psi}{d\xi^2} = \left(\frac{d^2h}{d\xi^2}-2\xi\frac{dh}{d\xi}+(\xi^2-1)h \right)e^{-\xi^2/2} \end{gather*}\]となるので、シュレーディンガー方程式($\ref{eqn:schrodinger_eqn_with_xi}$)は今
\[\frac{d^2h}{d\xi^2}-2\xi\frac{dh}{d\xi}+(K-1)h = 0 \label{eqn:schrodinger_eqn_with_h}\tag{10}\]となります。
べき級数展開
テイラーの定理(Taylor’s theorem)によれば、任意の滑らかに変化する関数はべき級数で表現できるので、式($\ref{eqn:schrodinger_eqn_with_h}$)の解を$\xi$の級数形式である
\[h(\xi) = a_0 + a_1\xi + a_2\xi^2 + \cdots = \sum_{j=0}^{\infty}a_j\xi^j \label{eqn:h_series_exp}\tag{11}\]の形で求めてみましょう。この級数の各項を微分すると、次の二つの式が得られます。
\[\begin{gather*} \frac{dh}{d\xi} = a_1 + 2a_2\xi + 3a_3\xi^2 + \cdots = \sum_{j=0}^{\infty}ja_j\xi^{j-1}, \\ \frac{d^2 h}{d\xi^2} = 2a_2 + 2\cdot3a_3\xi + 3\cdot4a_4\xi^2 + \cdots = \sum_{j=0}^{\infty} (j+1)(j+2)a_{j+2}\xi^j. \end{gather*}\]これら二つの式を再びシュレーディンガー方程式(式[$\ref{eqn:schrodinger_eqn_with_h}$])に代入すると、次を得ます。
\[\sum_{j=0}^{\infty}[(j+1)(j+2)a_{j+2} - 2ja_j + (K-1)a_j]\xi^j = 0. \label{eqn:schrodinger_eqn_power_series}\tag{12}\]べき級数展開の一意性により、$\xi$の各次数に対する係数は$0$でなければならないので
\[(j+1)(j+2)a_{j+2} - 2ja_j + (K-1)a_j = 0\] \[\therefore a_{j+2} = \frac{(2j+1-K)}{(j+1)(j+2)}a_j. \label{eqn:recursion_formula}\tag{13}\]この漸化式(recursion formula)はシュレーディンガー方程式と等価です。二つの任意の定数$a_0$と$a_1$が与えられれば、解$h(\xi)$のすべての項の係数を求めることができます。
しかし、このようにして得られた解を常に規格化できるわけではありません。もし級数$\sum a_j$が無限級数の場合($\lim_{j\to\infty} a_j\neq0$の場合)、非常に大きな$j$に対して上記の漸化式は近似的に
\[a_{j+2} \approx \frac{2}{j}a_j\]となり、これに対する近似的な解は
\[a_j \approx \frac{C}{(j/2)!} \quad \text{(}C\text{は任意の定数)}\]です。この場合、高次項が支配的になる大きな$\xi$値に対して
\[h(\xi) \approx C\sum\frac{1}{(j/2)!}\xi^j \approx C\sum\frac{1}{j!}\xi^{2j} \approx Ce^{\xi^2}\]の形になり、このように$h(\xi)$が$Ce^{\xi^2}$の形になると、式($\ref{eqn:psi_and_h}$)の$\psi(\xi)$は$Ce^{\xi^2/2}$の形になって$\xi \to \infty$のとき発散します。これは式($\ref{eqn:psi_approx}$)で$A=0, B\neq0$である規格化できない解に相当します。
したがって、級数$\sum a_j$は有限でなければなりません。ある「最大の」$j$値$n\in \mathbb{N}$が存在し、$j>n$のとき$a_j=0$でなければならず、このようになるためには$0$でない$a_n$に対して$a_{n+2}=0$でなければならないので、式($\ref{eqn:recursion_formula}$)から
\[K = 2n + 1\]でなければなりません。これを式($\ref{eqn:K}$)に代入すると、物理的に許容されるエネルギー
\[E_n = \left(n+\frac{1}{2} \right)\hbar\omega, \quad n=0,1,2,\dots \label{eqn:E_n}\tag{14}\]を得ます。これにより調和振動子の代数的解法の式(21)でのエネルギーの量子化条件を全く異なる方法を用いて同一に得ました。
エルミート多項式(Hermite polynomials)$H_n(\xi)$と定常状態$\psi_n(x)$
エルミート多項式$H_n$
一般的に$h_n(\xi)$は$\xi$の$n$次多項式で、$n$が偶数なら偶数次のみ、$n$が奇数なら奇数次のみを含みます。ここで前の係数($a_0$または$a_1$)を除いた残りをエルミート多項式(Hermite polynomials) $H_n(\xi)$と呼びます。
\[h_n(\xi) = \begin{cases} a_0 H_n(\xi), & n=2k & (k=0,1,2,\dots) \\ a_1 H_n(\xi), & n=2k+1 & (k=0,1,2,\dots) \end{cases}\]伝統的に$H_n$の最高次項の係数が$2^n$になるように任意に係数を定めます。
以下はエルミート多項式の最初の数個を示したものです。
\[\begin{align*} H_0 &= 1 \\ H_1 &= 2\xi \\ H_2 &= 4\xi^2 - 2 \\ H_3 &= 8\xi^3 - 12\xi \\ H_4 &= 16\xi^4 - 48\xi^2 + 12 \\ H_5 &= 32\xi^5 - 160\xi^3 + 120\xi \\ &\qquad\vdots \end{align*}\]定常状態$\psi_n(x)$
調和振動子に対する規格化された定常状態は次のとおりです。
\[\psi_n(x) = \left(\frac{m\omega}{\pi\hbar} \right)^{1/4} \frac{1}{\sqrt{2^n n!}}H_n(\xi)e^{-\xi^2/2}.\]これは調和振動子の代数的解法で求めた結果(式[27])と一致します。
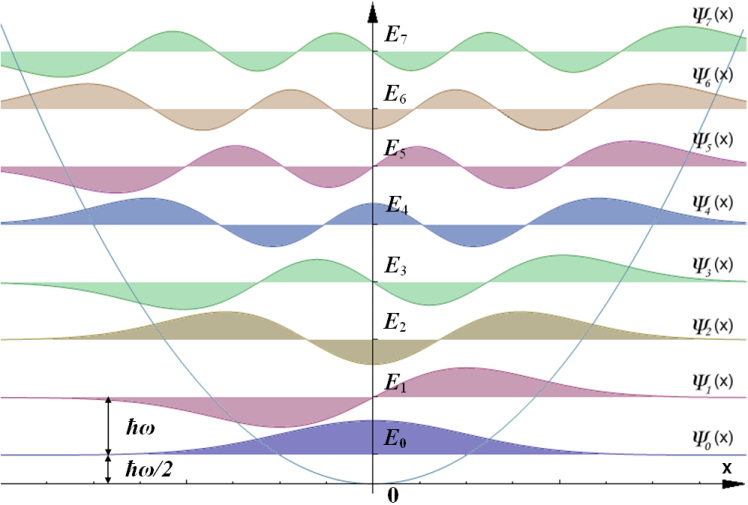
次の画像は最初の8つの$n$値に対する定常状態$\psi_n(x)$と確率密度$|\psi_n(x)|^2$を示したものです。量子振動子の固有関数として偶関数と奇関数が交互に現れることがわかります。
画像出典
- 作者:ウィキメディア・ユーザー AllenMcC
- ライセンス:CC BY-SA 3.0
画像出典
- 作者:ウィキメディア・ユーザー AllenMcC
- ライセンス:Public Domain
量子振動子は対応する古典的振動子とかなり異なり、エネルギーが量子化されているだけでなく、位置$x$の確率分布もまた奇妙な特性を示します。
- 古典力学的には存在し得ない領域(与えられた$E$に対する古典的な振幅より大きな$x$)でも発見される確率が$0$ではなく、低い確率ではあるが粒子が存在し得る
- $n$が奇数のすべての定常状態に対して、中心で粒子を発見する確率は$0$
$n$が大きくなるほど、量子振動子は古典的振動子に類似した様相を呈します。以下の画像は位置$x$の古典的な確率分布(点線)と$n=30$のときの量子状態$|\psi_{30}|^2$(実線)を示したものです。凸凹した部分を滑らかにつなぐと、二つのグラフはおおよそ一致する形を示します。
画像出典
- 作者:ウィキメディア・ユーザー AkanoToE
- ライセンス:Public Domain
量子振動子の確率分布のインタラクティブな可視化
以下は私が直接作成したPlotly.jsベースのレスポンシブな可視化です。スライダーで$n$値を調整しながら、位置$x$に対する古典的な確率分布および$|\psi_n|^2$の概形を確認できます。
また、もしご自身のコンピュータでPythonを使用でき、Numpy、Plotly、Dashライブラリがインストールされている環境であれば、同じリポジトリ内の/src/quantum_oscillator.py Pythonスクリプトを実行して結果を見ることもできます。