La particule libre (The Free Particle)

TL;DR

• Particule libre : $V(x)=0$, pas de conditions aux limites (énergie arbitraire)
• La solution à variables séparées $\Psi_k(x,t) = Ae^{i\left(kx-\frac{\hbar k^2}{2m}t \right)}$ diverge vers l’infini lors de l’intégration du carré et ne peut donc pas être normalisée, ce qui implique :
  • Une particule libre ne peut pas exister en état stationnaire
  • Une particule libre ne peut pas avoir une énergie définie comme une seule valeur précise (incertitude énergétique)
• Néanmoins, puisque la solution générale de l’équation de Schrödinger dépendante du temps est une combinaison linéaire des solutions à variables séparées, ces dernières conservent une importance mathématique. Cependant, en l’absence de conditions restrictives, la solution générale prend la forme d’une intégrale sur la variable continue $k$ plutôt qu’une somme ($\sum$) sur la variable discrète $n$.
• Solution générale de l’équation de Schrödinger :

\[\begin{gather*} \Psi(x,t) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{i(kx-\frac{\hbar k^2}{2m}t)}dk, \\ \text{où }\phi(k) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\Psi(x,0)e^{-ikx}dx \end{gather*}\]

• Relation entre incertitude de position et incertitude d’impulsion :
  • Quand l’incertitude de position diminue, l’incertitude d’impulsion augmente, et inversement
  • Il est impossible de connaître simultanément et précisément la position et l’impulsion d’une particule libre en mécanique quantique
• Vitesse de phase et vitesse de groupe de la fonction d’onde $\Psi(x,t)$ :
  • Vitesse de phase : $v_\text{phase} = \cfrac{\omega}{k} = \cfrac{\hbar k}{2m}$
  • Vitesse de groupe : $v_\text{group} = \cfrac{d\omega}{dk} = \cfrac{\hbar k}{m}$
• Signification physique de la vitesse de groupe et comparaison avec la mécanique classique :
  • Physiquement, la vitesse de groupe correspond à la vitesse de déplacement de la particule
  • Lorsque $\phi(k)$ a une forme très pointue autour d’une valeur $k_0$ (incertitude d’impulsion suffisamment petite),

\[v_\text{group} = v_\text{classical} = \sqrt{\cfrac{2E}{m}}\]

Prérequis

• Formule d’Euler
• Transformée de Fourier & théorème de Plancherel
• Équation de Schrödinger et fonction d’onde
• Équation de Schrödinger indépendante du temps
• Le puits carré infini unidimensionnel

Configuration du modèle

Examinons le cas le plus simple d’une particule libre ($V(x)=0$). Classiquement, il s’agit simplement d’un mouvement rectiligne uniforme, mais en mécanique quantique, ce problème est plus intéressant.
L’équation de Schrödinger indépendante du temps pour une particule libre est

\[-\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2}=E\psi \tag{1}\]

soit

\[\frac{d^2\psi}{dx^2} = -k^2\psi \text{, où }k\equiv \frac{\sqrt{2mE}}{\hbar} \label{eqn:t_independent_schrodinger_eqn}\tag{2}\]

Jusqu’ici, c’est identique à l’intérieur d’un puits carré infini avec un potentiel nul. Cependant, cette fois, écrivons la solution générale sous forme de fonctions exponentielles :

\[\psi(x) = Ae^{ikx} + Be^{-ikx}. \tag{3}\]

$Ae^{ikx} + Be^{-ikx}$ et $C\cos{kx}+D\sin{kx}$ sont des méthodes équivalentes pour exprimer la même fonction de $x$. Grâce à la formule d’Euler $e^{ix}=\cos{x}+i\sin{x}$,

\[\begin{align*} Ae^{ikx}+Be^{-ikx} &= A[\cos{kx}+i\sin{kx}] + B[\cos{(-kx)}+i\sin{(-kx)}] \\ &= A(\cos{kx}+i\sin{kx}) + B(\cos{kx}-i\sin{kx}) \\ &= (A+B)\cos{kx} + i(A-B)\sin{kx}. \end{align*}\]

En posant $C=A+B$, $D=i(A-B)$, on obtient

\[Ae^{ikx} + Be^{-ikx} = C\cos{kx}+D\sin{kx}. \blacksquare\]

Inversement, $A$ et $B$ s’expriment en fonction de $C$ et $D$ comme $A=\cfrac{C-iD}{2}$, $B=\cfrac{C+iD}{2}$.

En mécanique quantique, les fonctions exponentielles représentent des ondes en mouvement quand $V=0$ et sont les plus pratiques pour traiter les particules libres. En revanche, les fonctions sinus et cosinus facilitent la représentation d’ondes stationnaires et apparaissent naturellement dans le cas du puits carré infini.

Contrairement au puits carré infini, il n’y a cette fois aucune condition aux limites qui restreigne $k$ et $E$. Autrement dit, une particule libre peut avoir n’importe quelle énergie positive.

Solution à variables séparées et vitesse de phase

En ajoutant la dépendance temporelle $e^{-iEt/\hbar}$ à $\psi(x)$, on obtient

\[\Psi(x,t) = Ae^{ik\left(x-\frac{\hbar k}{2m}t \right)} + Be^{-ik\left(x+\frac{\hbar k}{2m}t \right)} \label{eqn:Psi_seperated_solution}\tag{4}\]

Toute fonction arbitraire de $x$ et $t$ dépendant de cette forme particulière $(x\pm vt)$ représente une onde qui se déplace dans la direction $\mp x$ à la vitesse $v$ sans changer de forme. Ainsi, le premier terme de l’équation ($\ref{eqn:Psi_seperated_solution}$) représente une onde se déplaçant vers la droite, et le second terme représente une onde de même longueur d’onde et vitesse de propagation mais d’amplitude différente se déplaçant vers la gauche. Comme ils ne diffèrent que par le signe devant $k$, on peut écrire

\[\Psi_k(x,t) = Ae^{i\left(kx-\frac{\hbar k^2}{2m}t \right)} \tag{5}\]

où la direction de propagation de l’onde selon le signe de $k$ est :

\[k \equiv \pm\frac{\sqrt{2mE}}{\hbar},\quad \begin{cases} k>0 \Rightarrow & \text{déplacement vers la droite}, \\ k<0 \Rightarrow & \text{déplacement vers la gauche}. \end{cases} \tag{6}\]

L’« état stationnaire » d’une particule libre est manifestement une onde progressive*, avec une longueur d’onde $\lambda = 2\pi/|k|$ et, selon la formule de de Broglie,

\[p = \frac{2\pi\hbar}{\lambda} = \hbar k \label{eqn:de_broglie_formula}\tag{7}\]

une impulsion correspondante.

*Il est physiquement contradictoire qu’un « état stationnaire » soit une onde progressive. La raison sera bientôt expliquée.

De plus, la vitesse de cette onde est :

\[v_{\text{phase}} = \left|\frac{\omega}{k}\right| = \frac{\hbar|k|}{2m} = \sqrt{\frac{E}{2m}}. \label{eqn:phase_velocity}\tag{8}\]

(Ici, $\omega$ est le coefficient $\cfrac{\hbar k^2}{2m}$ devant $t$.)

Cependant, cette fonction d’onde diverge vers l’infini lors de l’intégration du carré et ne peut donc pas être normalisée.

\[\int_{-\infty}^{\infty}\Psi_k^*\Psi_k dx = |A|^2\int_{-\infty}^{\infty}dx = \infty. \tag{9}\]

Autrement dit, pour une particule libre, la solution à variables séparées n'est pas un état physiquement possible. Une particule libre ne peut pas exister en état stationnaire et ne peut pas avoir une valeur d’énergie spécifique. En fait, intuitivement, il serait plus étrange qu’une onde stationnaire se forme sans aucune condition aux limites aux deux extrémités.

Obtention de la solution générale $\Psi(x,t)$ de l’équation de Schrödinger dépendante du temps

Néanmoins, cette solution à variables séparées conserve une importance significative car, indépendamment de l’interprétation physique, la solution générale de l’équation de Schrödinger dépendante du temps est une combinaison linéaire des solutions à variables séparées, ce qui lui confère une importance mathématique. Cependant, en l’absence de conditions restrictives, la solution générale prend la forme d’une intégrale ($\int$) sur la variable continue $k$ plutôt qu’une somme ($\sum$) sur la variable discrète $n$.

\[\Psi(x,t) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{i(kx-\frac{\hbar k^2}{2m}t)}dk. \label{eqn:Psi_general_solution}\tag{10}\]

Ici, $\cfrac{1}{\sqrt{2\pi}}\phi(k)dk$ joue le même rôle que $c_n$ dans l’équation (21) du post ‘Équation de Schrödinger indépendante du temps’.

Cette fonction d’onde peut être normalisée pour un $\phi(k)$ approprié, mais elle doit nécessairement avoir un domaine de $k$ et donc une plage d’énergies et de vitesses. Ceci est appelé un paquet d’ondes (wave packet).

Les fonctions sinus sont spatialement infiniment étendues et ne peuvent donc pas être normalisées. Cependant, en superposant plusieurs de ces ondes, elles peuvent être localisées par interférence et devenir normalisables.

Détermination de $\phi(k)$ en utilisant le théorème de Plancherel

Maintenant que nous connaissons la forme de $\Psi(x,t)$ (équation [$\ref{eqn:Psi_general_solution}$]), il suffit de déterminer $\phi(k)$ qui satisfait la fonction d’onde initiale

\[\Psi(x,0) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{ikx}dk \label{eqn:Psi_at_t_0}\tag{11}\]

Il s’agit d’un problème typique d’analyse de Fourier, et la réponse peut être obtenue par le théorème de Plancherel.

\[f(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} F(k)e^{ikx}dk \Longleftrightarrow F(k)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(x)e^{-ikx}dx. \label{eqn:plancherel_theorem}\tag{12}\]

$F(k)$ est appelée la transformée de Fourier de $f(x)$, et $f(x)$ est la transformée de Fourier inverse de $F(k)$. Comme on peut le voir facilement dans l’équation ($\ref{eqn:plancherel_theorem}$), la seule différence entre les deux est le signe de l’exposant. Bien sûr, il existe une condition restrictive selon laquelle seules les fonctions pour lesquelles l’intégrale existe sont autorisées.

La condition nécessaire et suffisante pour l’existence de $f(x)$ est que $\int_{-\infty}^{\infty}|f(x)|^2dx$ soit fini. Dans ce cas, $\int_{-\infty}^{\infty}|F(k)|^2dk$ est également fini, et

\[\int_{-\infty}^{\infty}|f(x)|^2 dx = \int_{-\infty}^{\infty}|F(k)|^2 dk\]

Certaines personnes appellent cette équation plutôt que l’équation ($\ref{eqn:plancherel_theorem}$) le théorème de Plancherel (Wikipédia le décrit également ainsi).

Dans notre cas, la condition physique que $\Psi(x,0)$ doit être normalisée garantit nécessairement l’existence de l’intégrale. Par conséquent, la solution quantique pour une particule libre est l’équation ($\ref{eqn:Psi_general_solution}$), où

\[\phi(k) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\Psi(x,0)e^{-ikx}dx \label{eqn:phi}\tag{13}\]

Cependant, en pratique, l’intégrale de l’équation ($\ref{eqn:Psi_general_solution}$) peut rarement être résolue analytiquement. On utilise généralement l’analyse numérique par ordinateur pour obtenir les valeurs.

Calcul de la vitesse de groupe du paquet d’ondes et interprétation physique

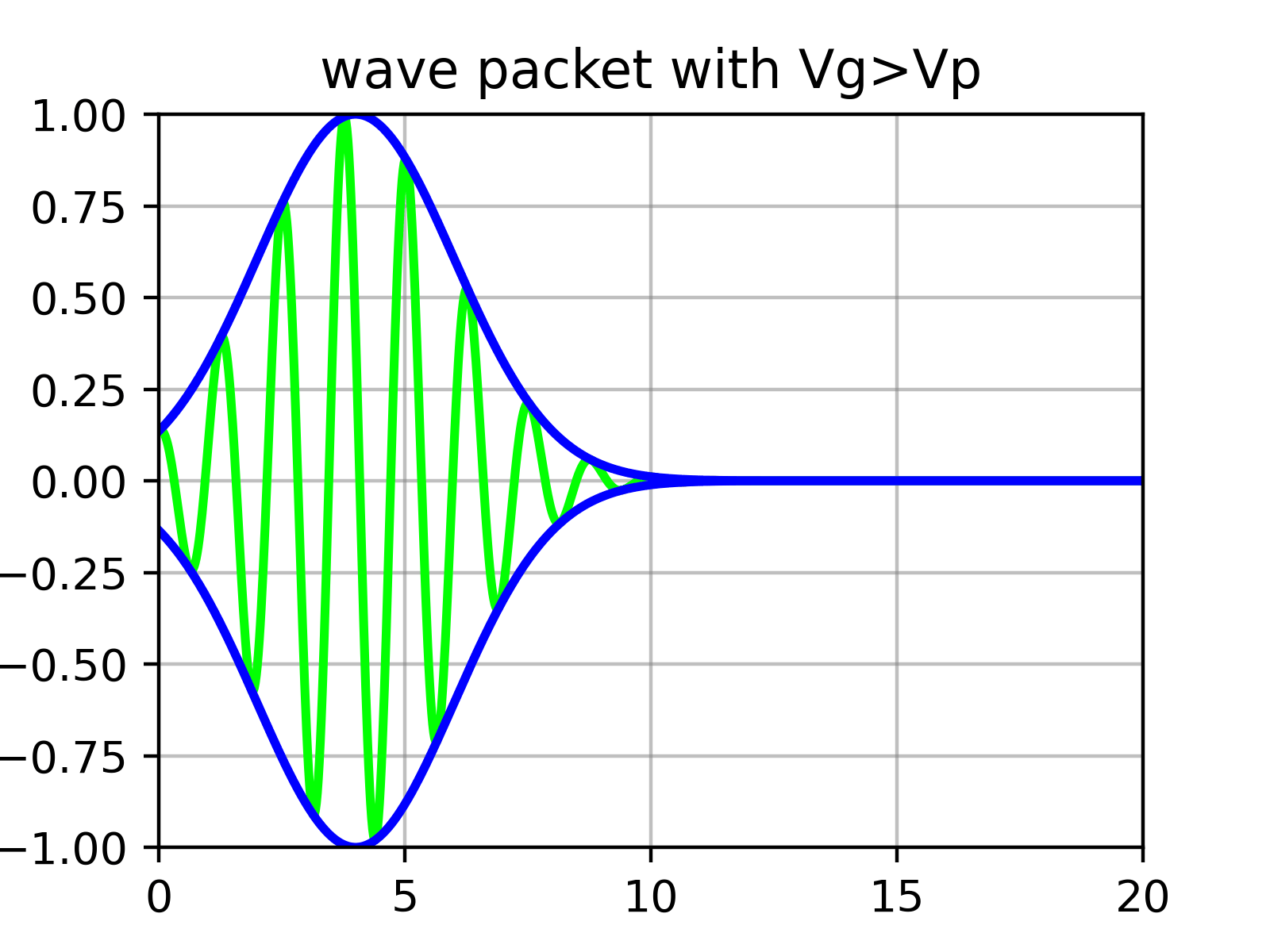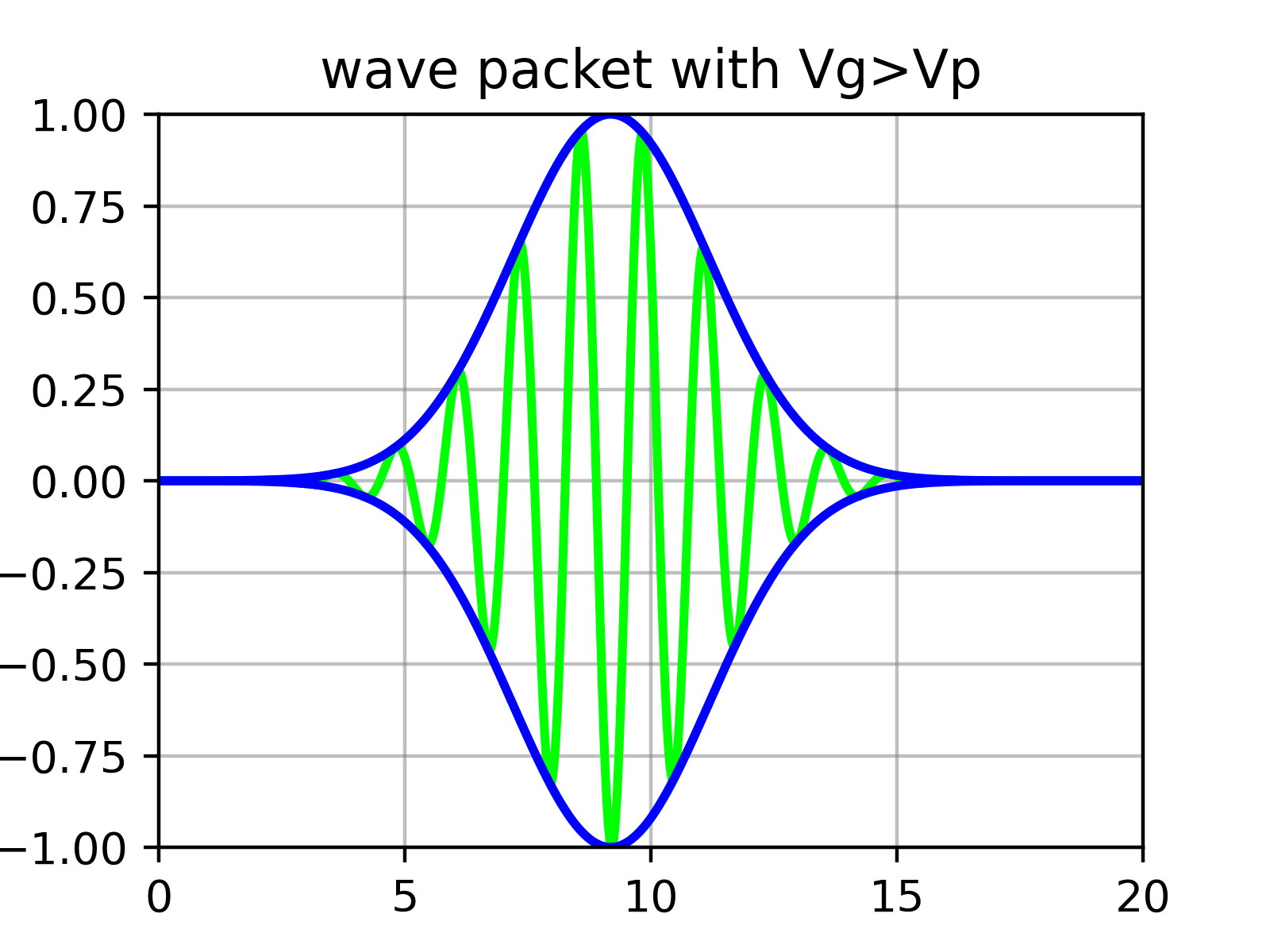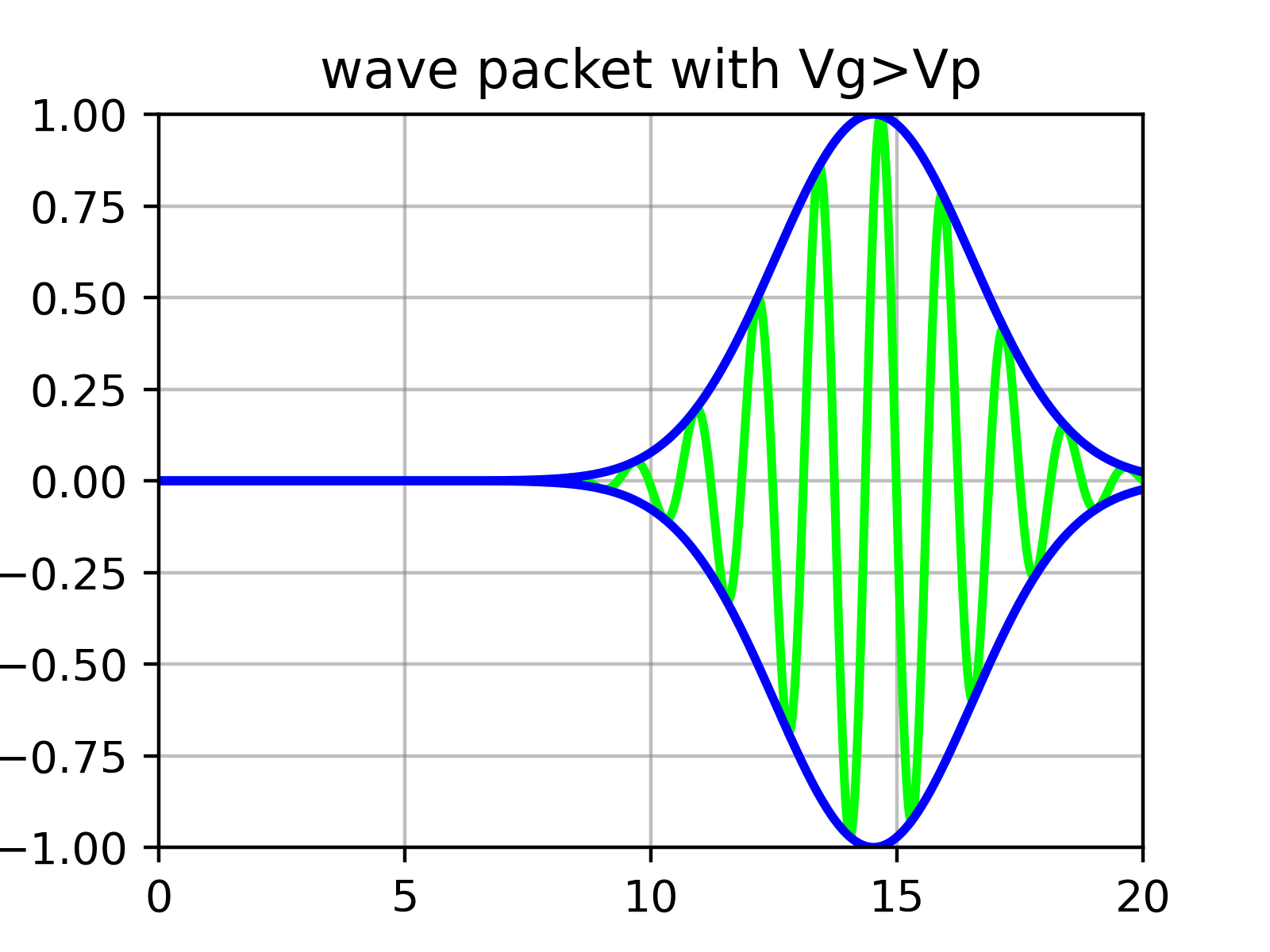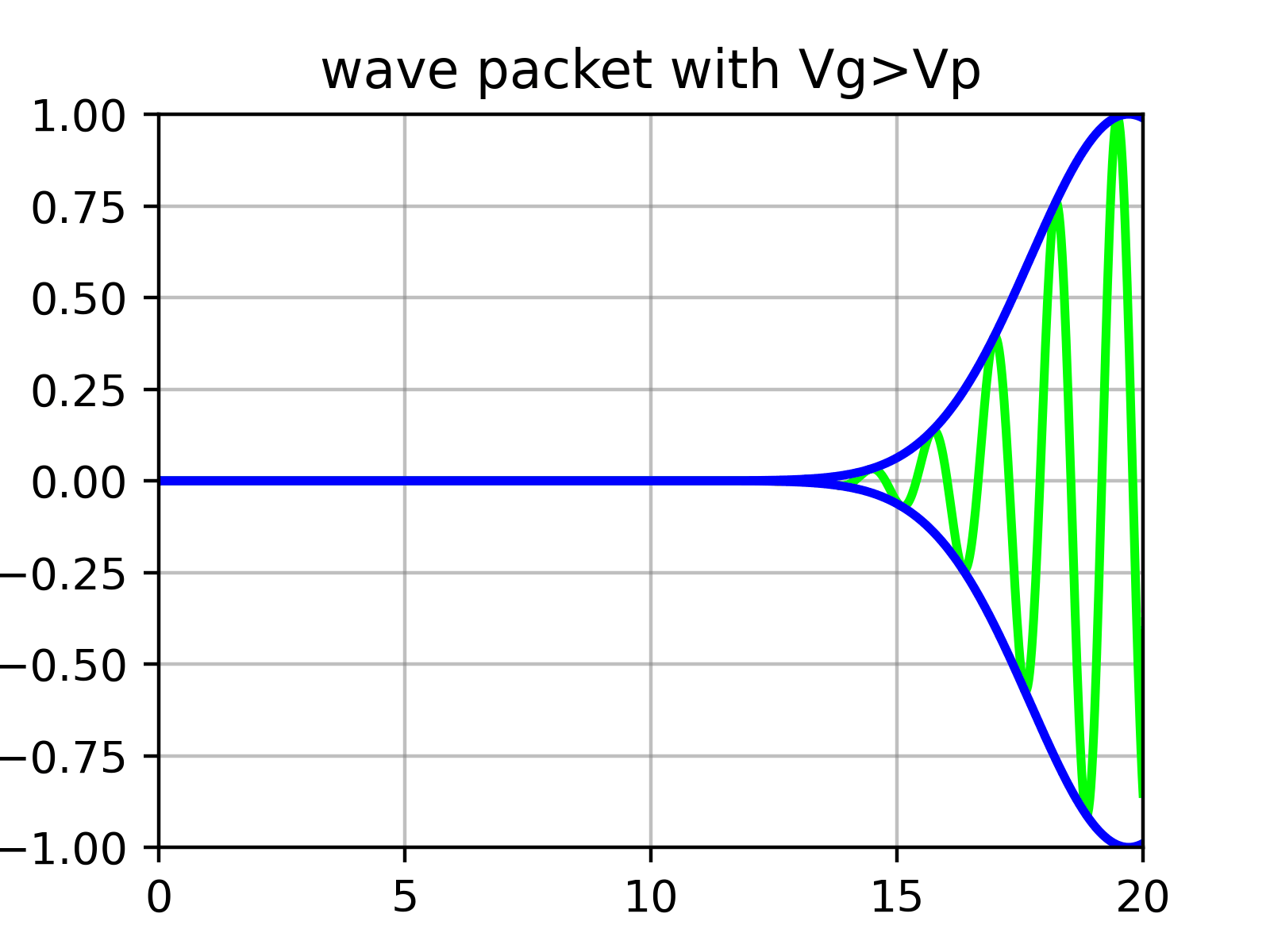
Essentiellement, un paquet d’ondes est la superposition de nombreuses fonctions sinus dont l’amplitude est déterminée par $\phi$. Autrement dit, il y a des « ondulations (ripples) » à l’intérieur de l’« enveloppe » qui forme le paquet d’ondes.

Licence d’image et attribution de la source originale

• Code source de génération d’image (gnuplot) : yunseo-kim/physics-visualizations
• Licence : Mozilla Public License 2.0
• Auteur original : Ph.D. Youjun Hu
• Attribution de licence originale : MIT License

Physiquement, ce qui correspond à la vitesse de la particule n’est pas la vitesse des ondulations individuelles (vitesse de phase) calculée précédemment dans l’équation ($\ref{eqn:phase_velocity}$), mais la vitesse de l’enveloppe extérieure (vitesse de groupe).

Relation entre incertitude de position et incertitude d’impulsion

Examinons la relation entre l’incertitude de position et l’incertitude d’impulsion en considérant séparément les parties intégrandes $\int\phi(k)e^{ikx}dk$ de l’équation ($\ref{eqn:Psi_at_t_0}$) et $\int\Psi(x,0)e^{-ikx}dx$ de l’équation ($\ref{eqn:phi}$).

Quand l’incertitude de position est petite

Lorsque $\Psi$ dans l’espace des positions est distribué dans une région très étroite $[x_0-\delta, x_0+\delta]$ autour d’une valeur $x_0$ et est proche de 0 en dehors de cette région (incertitude de position petite), $e^{-ikx} \approx e^{-ikx_0}$ est presque constant par rapport à $x$, donc

\[\begin{align*} \int_{-\infty}^{\infty} \Psi(x,0)e^{-ikx}dx &\approx \int_{x_0-\delta}^{x_0+\delta} \Psi(x,0)e^{-ikx_0}dx \\ &= e^{-ikx_0}\int_{x_0-\delta}^{x_0+\delta} \Psi(x,0)dx \\ &= e^{-ipx_0/\hbar}\int_{x_0-\delta}^{x_0+\delta} \Psi(x,0)dx \quad (\because \text{éqn. }\ref{eqn:de_broglie_formula}) \end{align*}\tag{14}\]

Le terme d’intégrale définie est constant par rapport à $p$, donc par le terme $e^{-ipx_0/\hbar}$ qui le précède, $\phi$ prend la forme d’une onde sinusoïdale par rapport à $p$ dans l’espace des impulsions, c’est-à-dire qu’elle est distribuée sur un large intervalle d’impulsions (incertitude d'impulsion grande).

Quand l’incertitude d’impulsion est petite

De même, lorsque $\phi$ dans l’espace des impulsions est distribué dans une région très étroite $[p_0-\delta, p_0+\delta]$ autour d’une valeur $p_0$ et est proche de 0 en dehors de cette région (incertitude d'impulsion petite), selon l’équation ($\ref{eqn:de_broglie_formula}$), $e^{ikx}=e^{ipx/\hbar} \approx e^{ip_0x/\hbar}$ est presque constant par rapport à $p$ et $dk=\frac{1}{\hbar}dp$, donc

\[\begin{align*} \int_{-\infty}^{\infty} \phi(k)e^{ikx}dk &= \frac{1}{\hbar}\int_{p_0-\delta}^{p_0+\delta} \phi(p)e^{ip_0x/\hbar}dp \\ &= \frac{1}{\hbar}e^{ip_0x/\hbar}\int_{p_0-\delta}^{p_0+\delta} \phi(p)dp \end{align*}\tag{15}\]

Par le terme $e^{ip_0x/\hbar}$ qui le précède, $\Psi$ prend la forme d’une onde sinusoïdale par rapport à $x$ dans l’espace des positions, c’est-à-dire qu’elle est distribuée sur un large intervalle de positions (incertitude de position grande).

Conclusion

Quand l’incertitude de position diminue, l’incertitude d’impulsion augmente, et inversement, quand l’incertitude d’impulsion diminue, l’incertitude de position augmente. Par conséquent, il est impossible de connaître simultanément et précisément la position et l’impulsion d’une particule libre en mécanique quantique.

Source de l’image

• Auteur : Utilisateur Wikipédia anglais Maschen
• Licence : domaine public

En fait, selon le principe d’incertitude, ceci s’applique non seulement aux particules libres mais à tous les cas. Le principe d’incertitude sera traité dans un post séparé ultérieurement.

Vitesse de groupe du paquet d’ondes

En réécrivant la solution générale de l’équation ($\ref{eqn:Psi_general_solution}$) avec $\omega \equiv \cfrac{\hbar k^2}{2m}$ comme dans l’équation ($\ref{eqn:phase_velocity}$), on obtient

\[\Psi(x,t) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{i(kx-\omega t)}dk \tag{16}\]

L’équation comme $\omega = \cfrac{\hbar k^2}{2m}$ qui exprime $\omega$ en fonction de $k$ est appelée relation de dispersion. Le contenu qui suit s’applique généralement à tous les paquets d’ondes, quelle que soit la relation de dispersion.

Supposons maintenant que $\phi(k)$ ait une forme très pointue autour d’une valeur appropriée $k_0$. (Il peut aussi être largement étalé par rapport à $k$, mais dans ce cas, la forme du paquet d’ondes se déforme très rapidement et change vers une autre forme. Comme les composantes pour différents $k$ se déplacent chacune à des vitesses différentes, elles perdent le sens d’un « groupe » global ayant une vitesse bien définie. Autrement dit, l'incertitude d'impulsion augmente.)
La fonction intégrée peut être négligée sauf autour de $k_0$, donc on peut développer la fonction $\omega(k)$ en série de Taylor autour de ce point, et en ne gardant que le terme du premier ordre :

\[\omega(k) \approx \omega_0 + \omega_0^\prime(k-k_0)\]

En substituant $s=k-k_0$ et en intégrant autour de $k_0$ :

\[\begin{align*} \Psi(x,t) &= \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\phi(k_0+s)e^{i[(k_0+s)x-(\omega_0+\omega_0^\prime s)t]}ds \\ &= \frac{1}{\sqrt{2\pi}}e^{i(k_0x-\omega_0t)}\int_{-\infty}^{\infty}\phi(k_0+s)e^{is(x-\omega_0^\prime t)}ds. \end{align*}\tag{17}\]

Le terme de devant $e^{i(k_0x-\omega_0t)}$ représente une onde sinusoïdale (« ondulations ») se déplaçant à la vitesse $\omega_0/k_0$, et le terme intégral (« enveloppe ») qui détermine l’amplitude de cette onde sinusoïdale se déplace à la vitesse $\omega_0^\prime$ par la partie $e^{is(x-\omega_0^\prime t)}$. Par conséquent, la vitesse de phase en $k=k_0$ est

\[v_\text{phase} = \frac{\omega_0}{k_0} = \frac{\omega}{k} = \frac{\hbar k}{2m} \tag{18}\]

ce qui confirme à nouveau la valeur de l’équation ($\ref{eqn:phase_velocity}$), et la vitesse de groupe est

\[v_\text{group} = \omega_0^\prime = \frac{d\omega}{dk} = \frac{\hbar k}{m} \label{eqn:group_velocity}\tag{19}\]

soit le double de la vitesse de phase.

Comparaison avec la mécanique classique

Sachant que la mécanique classique est valide à l’échelle macroscopique, les résultats obtenus par la mécanique quantique doivent pouvoir être approximés par les résultats de calcul de la mécanique classique lorsque l’incertitude quantique est suffisamment petite. Dans le cas de la particule libre que nous traitons, lorsque $\phi(k)$ a une forme très pointue autour d’une valeur appropriée $k_0$ comme supposé précédemment (c’est-à-dire, lorsque l'incertitude d'impulsion est suffisamment petite), la vitesse de groupe $v_\text{group}$ qui correspond à la vitesse de la particule en mécanique quantique doit être égale à la vitesse de la particule $v_\text{classical}$ obtenue en mécanique classique pour les mêmes valeurs de $k$ et d’énergie $E$ correspondante.

En substituant $k\equiv \cfrac{\sqrt{2mE}}{\hbar}$ de l’équation ($\ref{eqn:t_independent_schrodinger_eqn}$) dans la vitesse de groupe que nous venons de calculer (équation [$\ref{eqn:group_velocity}$]) :

\[v_\text{quantum} = \sqrt{\frac{2E}{m}} \tag{20}\]

et la vitesse d’une particule libre ayant une énergie cinétique $E$ en mécanique classique est également :

\[v_\text{classical} = \sqrt{\frac{2E}{m}} \tag{21}\]

Par conséquent, $v_\text{quantum}=v_\text{classical}$, ce qui confirme que le résultat obtenu en appliquant la mécanique quantique est une solution physiquement valide.