Transfert d'énergie par collision

TL;DR

• L’énergie totale et la quantité de mouvement sont conservées lors des collisions
• Les ions ayant perdu tous leurs électrons et les électrons n’ont que de l’énergie cinétique
• Les atomes neutres et les ions n’ayant perdu que certains électrons ont une énergie interne, et peuvent subir une excitation, une désexcitation ou une ionisation selon les changements d’énergie potentielle
• Classification des types de collision selon les changements d’énergie cinétique avant et après la collision :
  • Collision élastique : la quantité totale d’énergie cinétique reste constante avant et après la collision
  • Collision inélastique : perte d’énergie cinétique pendant le processus de collision
    • Excitation
    • Ionisation
  • Collision superélastique : augmentation de l’énergie cinétique pendant le processus de collision
    • Désexcitation
• Taux de transfert d’énergie par collision élastique :
  • Taux de transfert d’énergie par collision individuelle : $\zeta_L = \cfrac{4m_1m_2}{(m_1+m_2)^2}\cos^2\theta_2$
  • Taux moyen de transfert d’énergie par collision : $\overline{\zeta_L} = \cfrac{4m_1m_2}{(m_1+m_2)^2}\overline{\cos^2\theta_2} = \cfrac{2m_1m_2}{(m_1+m_2)^2}$
    • Quand $m_1 \approx m_2$ : $\overline{\zeta_L} \approx \cfrac{1}{2}$, un transfert d’énergie efficace se produit, atteignant rapidement l’équilibre thermique
    • Quand $m_1 \ll m_2$ ou $m_1 \gg m_2$ : $\overline{\zeta_L} \approx 10^{-5}\sim 10^{-4}$, l’efficacité du transfert d’énergie est très faible, rendant difficile l’atteinte de l’équilibre thermique. C’est la raison pour laquelle dans un plasma faiblement ionisé, $T_e \gg T_i \approx T_n$, avec une grande différence entre la température des électrons et celle des ions et des atomes neutres.
• Taux de transfert d’énergie par collision inélastique :
  • Taux maximal de conversion en énergie interne par collision unique : $\zeta_L = \cfrac{\Delta U_\text{max}}{\cfrac{1}{2}m_1v_1^2} = \cfrac{m_2}{m_1+m_2}\cos^2\theta_2$
  • Taux moyen maximal de conversion en énergie interne : $\overline{\zeta_L} = \cfrac{m_2}{m_1+m_2}\overline{\cos^2\theta_2} = \cfrac{m_2}{2(m_1+m_2)}$
    • Quand $m_1 \approx m_2$ : $\overline{\zeta_L} \approx \cfrac{1}{4}$
    • Quand $m_1 \gg m_2$ : $\overline{\zeta_L} \approx 10^{-5}\sim 10^{-4}$
    • Quand $m_1 \ll m_2$ : $\overline{\zeta_L} = \cfrac{1}{2}$, c’est le cas le plus efficace pour augmenter l’énergie interne de la cible de collision (ion ou atome neutre) et la mettre dans un état excité. C’est la raison pour laquelle l’ionisation (création de plasma), l’excitation (émission de lumière) et la dissociation des molécules (création de radicaux) par les électrons se produisent facilement.

Prérequis

• Constituants des particules subatomiques et des atomes

Collisions entre particules dans un plasma

• L’énergie totale et la quantité de mouvement sont conservées lors des collisions
• Les ions ayant perdu tous leurs électrons et les électrons n’ont que de l’énergie cinétique
• Les atomes neutres et les ions n’ayant perdu que certains électrons ont une énergie interne, et peuvent subir une excitation, une désexcitation ou une ionisation selon les changements d’énergie potentielle
• Classification des types de collision selon les changements d’énergie cinétique avant et après la collision :
  • Collision élastique : la quantité totale d’énergie cinétique reste constante avant et après la collision
  • Collision inélastique : perte d’énergie cinétique pendant le processus de collision
    • Excitation
    • Ionisation
  • Collision superélastique : augmentation de l’énergie cinétique pendant le processus de collision
    • Désexcitation

Transfert d’énergie par collision élastique

Taux de transfert d’énergie par collision individuelle

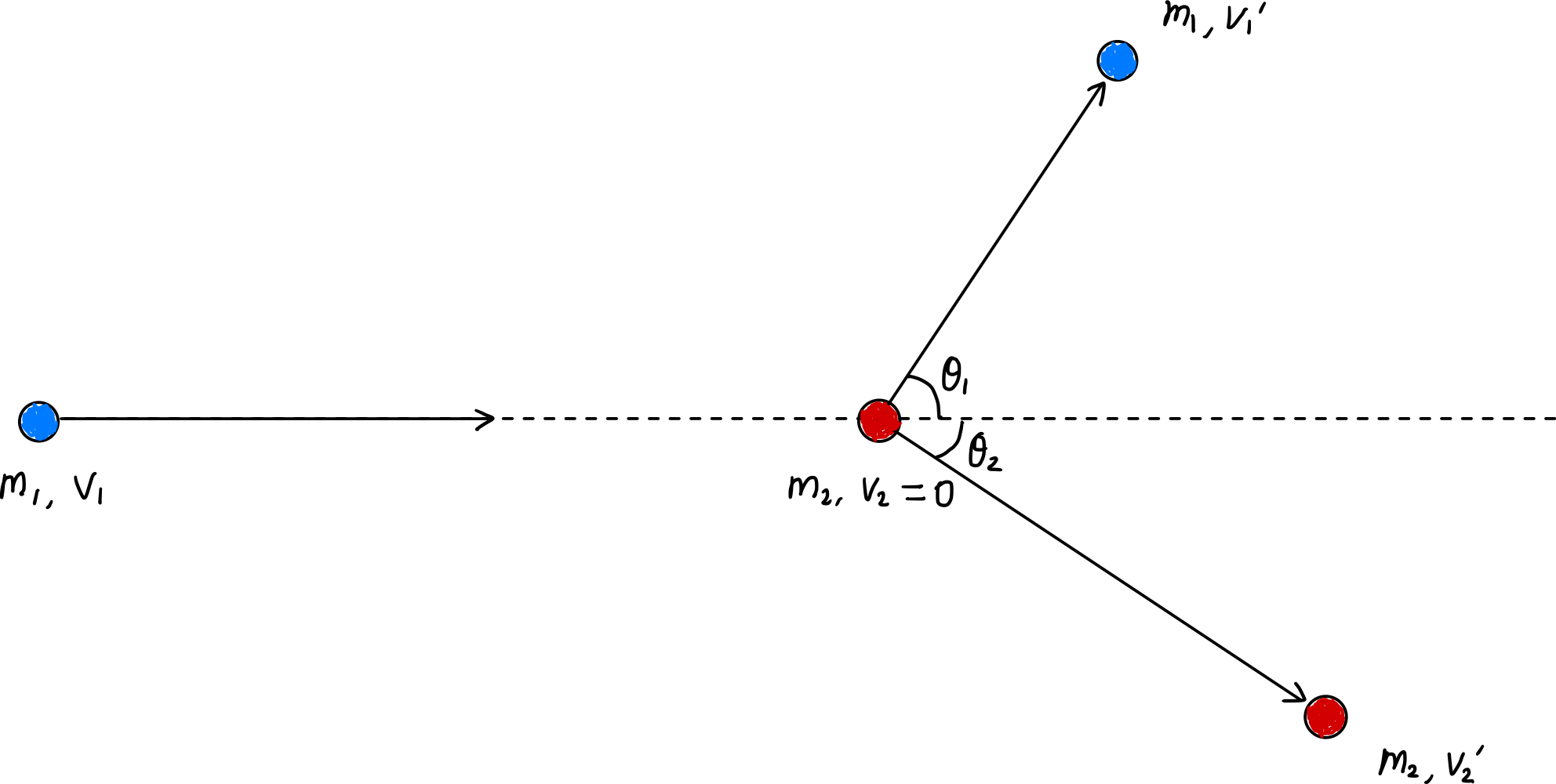
Dans une collision élastique, la quantité de mouvement et l’énergie cinétique sont conservées avant et après la collision.

En établissant les équations de conservation de la quantité de mouvement pour les axes $x$ et $y$ respectivement, on obtient :

\[\begin{gather*} m_1v_1 = m_1v_1^{\prime}\cos\theta_1 + m_2v_2^{\prime}\cos\theta_2, \label{eqn:momentum_conservation_x}\tag{1} \\ m_1v_1^{\prime}\sin\theta_1 = m_2v_2^{\prime}\sin\theta_2 \label{eqn:momentum_conservation_y}\tag{2} \end{gather*}\]

De plus, par conservation de l’énergie :

\[\frac{1}{2}m_1v_1^2 = \frac{1}{2}m_1{v_1^{\prime}}^2 + \frac{1}{2}m_2{v_2^{\prime}}^2\] \[v_1^2 = {v_1^{\prime}}^2 + \frac{m_2}{m_1}{v_2^{\prime}}^2 \label{eqn:energy_conservation}\tag{3}\]

De l’équation ($\ref{eqn:momentum_conservation_x}$), on obtient :

\[m_1 v_1^{\prime} \cos \theta_1 = m_1v_1 - m_2v_2^{\prime} \cos \theta_2 \label{eqn:momentum_conservation_x_2}\tag{4}\]

En élevant au carré les deux côtés des équations ($\ref{eqn:momentum_conservation_y}$) et ($\ref{eqn:momentum_conservation_x_2}$) et en les additionnant, on obtient :

\[\begin{align*} (m_1v_1^{\prime})^2 &= (m_2 v_2^\prime \sin \theta_2)^2 + (m_1 v_1 - m_2 v_2^\prime \cos \theta_2)^2 \\ &= m_1^2 v_1^2 - 2 m_1 m_2 v_1 v_2^\prime \cos \theta_2 + m_2^2 {v_2^\prime}^2 \tag{5} \end{align*}\]

En divisant les deux côtés par $m_1^2$, on obtient :

\[{v_1^{\prime}}^2 = v_1^2 - 2 \frac{m_2}{m_1} v_1 v_2^\prime \cos \theta_2 + \left(\frac{m_2}{m_1}\right)^2 {v_2^\prime}^2 \label{eqn:momentum_conservation}\tag{6}\]

En substituant l’équation ($\ref{eqn:energy_conservation}$) dans celle-ci, on peut la réorganiser comme suit :

\[\begin{gather*} \left( \frac{m_2}{m_1} \right) {v_2^\prime}^2 = 2 \left( \frac{m_2}{m_1} \right) v_1 v_2^\prime \cos \theta_2 - \left( \frac{m_2}{m_1} \right)^2 {v_2^\prime}^2 \\ 2v_1 \cos \theta_2 = \left(\frac{m_1 + m_2}{m_1} \right) v_2^\prime \\ v_2^{\prime} = \frac{2m_1v_1\cos\theta_2}{m_1 + m_2}. \label{eqn:v_2_prime}\tag{7} \end{gather*}\]

À partir de cela, on obtient le taux de transfert d’énergie $\zeta_L$ comme suit :

\[\begin{align*} \therefore \zeta_L &= \frac{\cfrac{1}{2}m_2{v_2^\prime}^2}{\cfrac{1}{2}m_1v_1^2} = \frac{m_2}{m_1v_1^2} {\left(\frac{2m_1v_1\cos\theta_2}{m_1 + m_2} \right)}^2 \\ &= \frac{4m_1m_2}{(m_1+m_2)^2}\cos^2\theta_2. \quad \blacksquare \label{eqn:elastic_E_transfer_rate}\tag{8} \end{align*}\]

Taux moyen de transfert d’énergie par collision

Pour les angles de 0 à 2π, $\sin^2{\theta_2}+\cos^2{\theta_2}=1$ et $\overline{\sin^2{\theta_2}}=\overline{\cos^2{\theta_2}}$, donc :

\[\begin{align*} \overline{\cos^2{\theta_2}} &= \overline{(1-\sin^2{\theta_2})} = 1 - \overline{\sin^2{\theta_2}} \\ &= 1 - \overline{\cos^2{\theta_2}} \end{align*}\] \[\begin{gather*} 2 \cdot \overline{\cos^2{\theta_2}} = 1 \\ \overline{\cos^2{\theta_2}} = \frac{1}{2}. \end{gather*}\]

En substituant ceci dans l’équation ($\ref{eqn:elastic_E_transfer_rate}$) précédemment obtenue, on obtient :

\[\overline{\zeta_L} = \frac{4m_1m_2}{(m_1+m_2)^2}\overline{\cos^2\theta_2} = \frac{2m_1m_2}{(m_1+m_2)^2}. \quad \blacksquare \label{eqn:elastic_E_mean_transfer_rate}\tag{9}\]

Quand $m_1 \approx m_2$

Cela s’applique aux collisions électron-électron, ion-ion, atome neutre-atome neutre, et ion-atome neutre. Dans ce cas :

\[\overline{\zeta_L} = \frac{2m_1m_2}{(m_1+m_2)^2} \approx \frac{1}{2} \label{eqn:elastic_similar_m}\tag{10}\]

Un transfert d’énergie efficace se produit, atteignant rapidement l’équilibre thermique.

Quand $m_1 \ll m_2$ ou $m_1 \gg m_2$

Cela s’applique aux collisions électron-ion, électron-atome neutre, ion-électron, et atome neutre-électron. Dans ces cas :

\[\overline{\zeta_L} = \frac{2m_1m_2}{(m_1+m_2)^2} \approx \frac{2m_1}{m_2}\text{ (basé sur }m_1 \ll m_2 \text{)} \approx 10^{-5}\sim 10^{-4} \label{eqn:elastic_different_m}\tag{11}\]

L’efficacité du transfert d’énergie est très faible, rendant difficile l’atteinte de l’équilibre thermique. C’est la raison pour laquelle dans un plasma faiblement ionisé, $T_e \gg T_i \approx T_n$, avec une grande différence entre la température des électrons et celle des ions et des atomes neutres.

Transfert d’énergie par collision inélastique

Taux maximal de conversion en énergie interne par collision unique

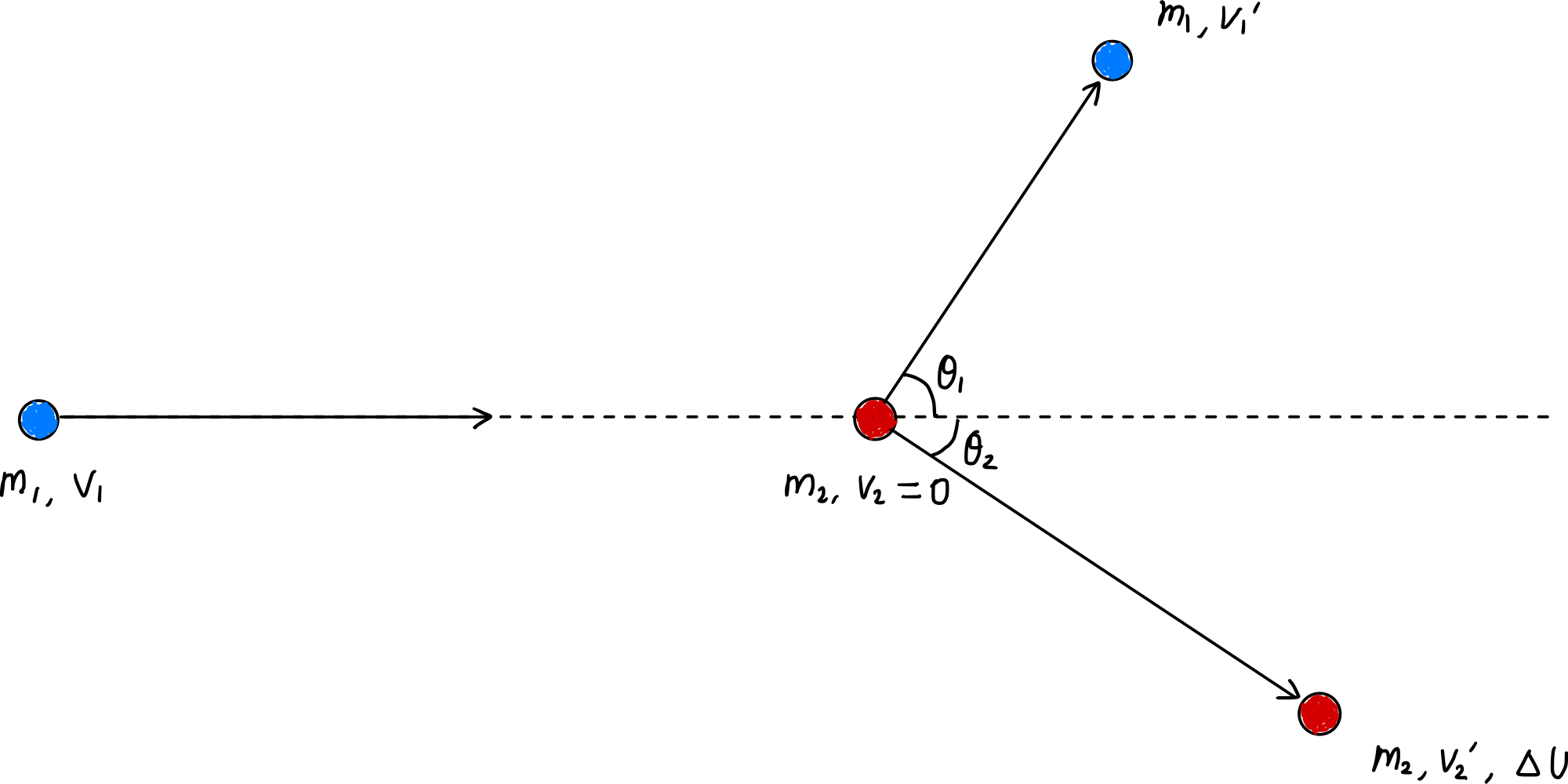
La conservation de la quantité de mouvement (équation [$\ref{eqn:momentum_conservation}$]) s’applique également dans ce cas, mais l’énergie cinétique n’est pas conservée car il s’agit d’une collision inélastique. Dans ce cas, l’énergie cinétique perdue par la collision inélastique est convertie en énergie interne $\Delta U$, donc :

\[\Delta U = \frac{1}{2} m_1 v_1^2 - \left( \frac{1}{2} m_1 {v_1^{\prime}}^2 + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right) \label{eqn:delta_U}\tag{12}\]

En substituant l’équation ($\ref{eqn:momentum_conservation}$) dans celle-ci et en réorganisant, on obtient :

\(\begin{align*} \Delta U &= \frac{1}{2} m_1 v_1^2 - \left[ \frac{1}{2} m_1 \left( v_1^2 - 2 \frac{m_2}{m_1} v_1 v_2^{\prime} \cos \theta_2 + \left( \frac{m_2}{m_1} v_2^{\prime} \right)^2 \right) + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right] \\ &= \frac{1}{2} m_1 v_1^2 - \left[ \frac{1}{2} m_1 v_1^2 - m_2 v_1 v_2^{\prime} \cos \theta_2 + \frac{1}{2} \frac{m_2^2}{m_1} {v_2^{\prime}}^2 + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right] \\ &= m_2 v_1 v_2^{\prime} \cos \theta_2 - \frac{1}{2}m_2{v_2^{\prime}}^2\left(\frac{m_1 + m_2}{m_1}\right) \label{eqn:delta_U_2}\tag{13} \end{align*}\).

En différenciant $\Delta U$ par rapport à $v_2^\prime$, et en trouvant le point extrême où la dérivée est égale à zéro et sa valeur maximale, on obtient :

\[\cfrac{d \Delta U}{d v_2^{\prime}} = m_2 v_1 \cos \theta_2 - m_2 v_2^{\prime} \left( \frac{m_1 + m_2}{m_1} \right) = 0 \tag{14}\] \[\begin{gather*} v_2^{\prime} \left( \frac{m_1 + m_2}{m_1} \right) = v_1 \cos \theta_2 \\ v_2^\prime = \frac{m_1v_1\cos\theta_2}{m_1+m_2}. \end{gather*}\] \[\therefore v_2^{\prime} = \frac{m_1v_1\cos\theta_2}{m_1+m_2} \text{ quand } \Delta U_\text{max} = \frac{1}{2}\frac{m_1m_2 v_1^2 \cos^2\theta_2}{m_1 + m_2}. \label{eqn:delta_U_max}\tag{15}\]

À partir de cela, le taux maximal de conversion de l’énergie cinétique en énergie interne $\zeta_L$ possible par une seule collision inélastique est :

\[\zeta_L = \frac{\Delta U_\text{max}}{\cfrac{1}{2}m_1v_1^2} = \frac{m_2}{m_1+m_2}\cos^2\theta_2. \quad \blacksquare \label{eqn:inelastic_E_transfer_rate}\tag{16}\]

Taux moyen maximal de conversion en énergie interne

De même, en substituant $\overline{\cos^2{\theta_2}} = \cfrac{1}{2}$ dans l’équation ($\ref{eqn:inelastic_E_transfer_rate}$), on obtient :

\[\overline{\zeta_L} = \frac{m_2}{m_1+m_2}\overline{\cos^2\theta_2} = \frac{m_2}{2(m_1+m_2)}. \label{eqn:inelastic_E_mean_transfer_rate}\tag{17}\]

Quand $m_1 \approx m_2$

Cela s’applique aux collisions ion-ion, ion-atome neutre, et atome neutre-atome neutre.

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} = \frac{1}{4}. \label{eqn:inelastic_similar_m}\tag{18}\]

Quand $m_1 \gg m_2$

Cela s’applique aux collisions ion-électron et atome neutre-électron.

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} \approx \frac{m_2}{2m_1} \approx 10^{-5}\sim 10^{-4}. \label{eqn:inelastic_ion_electron}\tag{19}\]

Quand $m_1 \ll m_2$

Cela s’applique aux collisions électron-ion et électron-atome neutre. Alors que les deux cas précédents ne diffèrent pas beaucoup des collisions élastiques, ce troisième cas montre une différence importante. Dans ce cas :

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} \approx \frac{m_2}{2m_2} = \frac{1}{2} \label{eqn:inelastic_electron_ion}\tag{20}\]

C’est le cas le plus efficace pour augmenter l’énergie interne de la cible de collision (ion ou atome neutre) et la mettre dans un état excité. C’est la raison pour laquelle, comme nous le verrons plus tard, l’ionisation par les électrons (création de plasma), l’excitation (émission de lumière) et la dissociation des molécules (création de radicaux) se produisent facilement.