Définition du plasma, concept de température et équation de Saha

TL;DR

• Plasma : Gaz quasi-neutre composé de particules chargées et neutres présentant un comportement collectif
• ‘Comportement collectif’ du plasma :
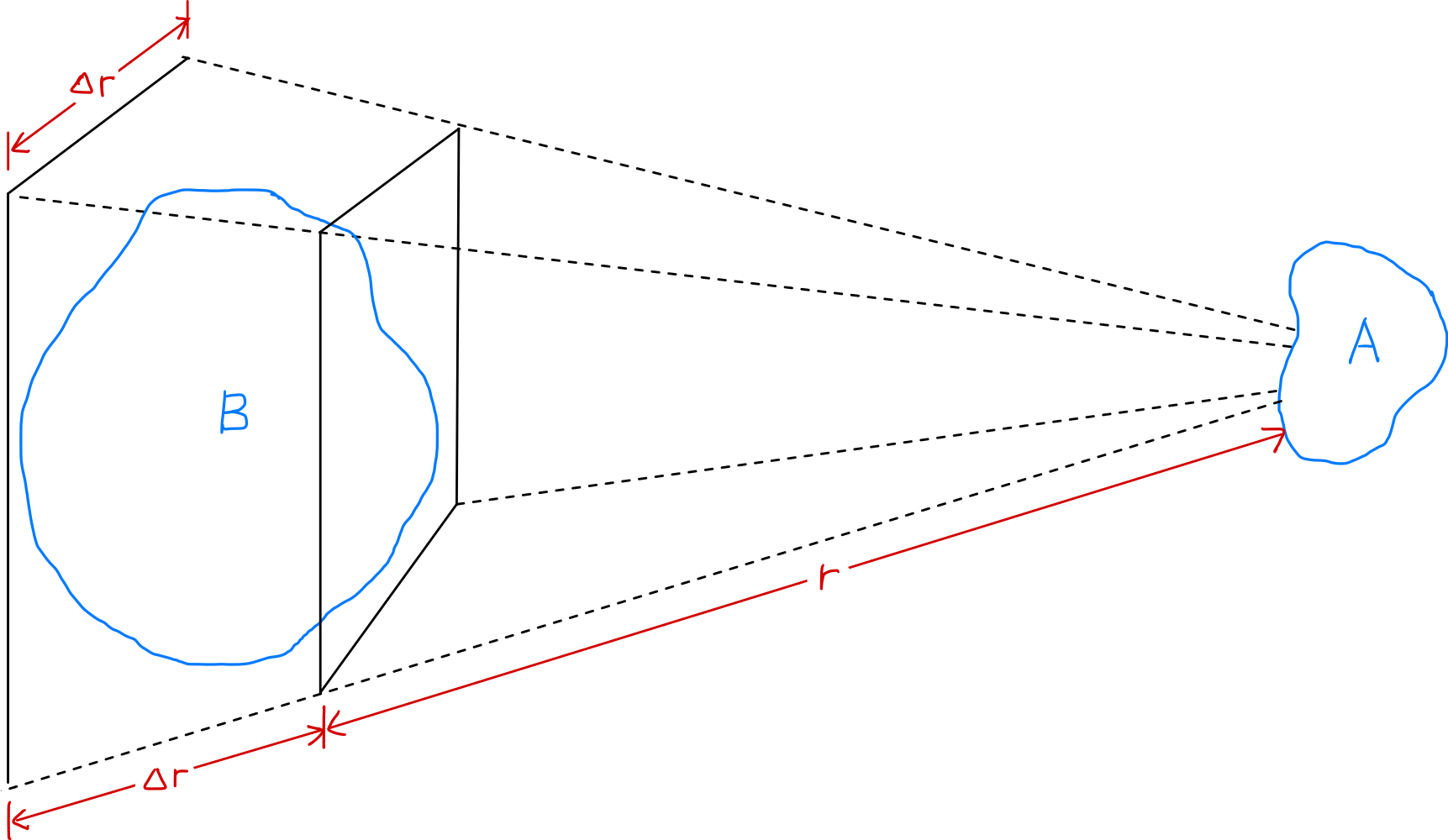
  • La force électrique entre deux régions A et B du plasma diminue en $1/r^2$ avec la distance
  • Cependant, pour un angle solide donné ($\Delta r/r$), le volume de la région B du plasma pouvant influencer A augmente en $r^3$
  • Ainsi, les parties constituantes du plasma peuvent exercer des forces significatives les unes sur les autres même à grande distance
• Équation de Saha : Relation entre l’état d’ionisation, la température et la pression d’un gaz en équilibre thermique

\[\frac{n_{i+1}n_e}{n_i} = \frac{2}{\lambda_{\text{th}}^3}\frac{g_{i+1}}{g_i}\exp{\left[-\frac{\epsilon_{i+1}-\epsilon_i}{k_B T}\right]}\]

• Concept de température en physique des plasmas :
  • L’énergie cinétique moyenne par particule dans les gaz et les plasmas est étroitement liée à la température, ces deux grandeurs étant interchangeables
  • En physique des plasmas, il est courant d’exprimer la température en $\mathrm{eV}$, unité d’énergie, comme la valeur de $kT$
    • $1\mathrm{eV}=11600\mathrm{K}$
  • Un plasma peut avoir simultanément plusieurs températures différentes, en particulier la température électronique ($T_e$) et la température ionique ($T_i$) peuvent être très différentes selon les cas
• Plasma froid vs. plasma chaud :
  • Température du plasma :
    • Plasma froid : $T_e \text{(>10,000℃)} \gg T_i \approx T_g \text{(}\sim\text{100℃)}$ $\rightarrow$ Plasma hors équilibre (non-equilibrium plasma)
    • Plasma (thermique) chaud : $T_e \approx T_i \approx T_g \text{(>10,000℃)}$ $\rightarrow$ Plasma en équilibre (equilibrium plasma)
  • Densité du plasma :
    • Plasma froid : $n_g \gg n_i \approx n_e$ $\rightarrow$ Faible taux d’ionisation, majoritairement composé de particules neutres
    • Plasma (thermique) chaud : $n_g \approx n_i \approx n_e $ $\rightarrow$ Taux d’ionisation élevé
  • Capacité thermique du plasma :
    • Plasma froid : Bien que la température électronique soit élevée, la densité est faible et la majorité des particules sont neutres à température relativement basse, donc la capacité thermique est faible et le plasma n’est pas chaud
    • Plasma (thermique) chaud : Les électrons, les ions et les particules neutres sont tous à haute température, donc la capacité thermique est élevée et le plasma est chaud

Prérequis

• Constituants de l’atome et particules subatomiques
• Distribution de Maxwell-Boltzmann (mécanique statistique)
• Masse et énergie, particules et ondes
• Symétries et lois de conservation (mécanique quantique), dégénérescence

Définition du plasma

Dans les textes expliquant le plasma à des non-spécialistes, le plasma est généralement défini comme suit :

Le quatrième état de la matière, après les états solide, liquide et gazeux, obtenu en chauffant un gaz à des températures extrêmement élevées jusqu’à ce que ses atomes constitutifs se séparent en électrons et ions positifs.

Ce n’est pas faux, et c’est ainsi que le site web de l’Institut coréen de l’énergie de fusion (Korea Institute of Fusion Energy) le présente également. C’est aussi la définition populaire qu’on trouve facilement en recherchant sur le plasma.

Cependant, bien que cette expression soit correcte, elle ne peut être considérée comme une définition rigoureuse. Même les gaz dans notre environnement à température et pression ambiantes sont légèrement ionisés, bien qu’à un taux extrêmement faible, mais on ne les appelle pas pour autant des plasmas. Lorsqu’une substance à liaison ionique comme le chlorure de sodium est dissoute dans l’eau, elle se sépare en ions chargés, mais cette solution n’est pas non plus un plasma.
En d’autres termes, bien qu’il soit vrai que le plasma soit un état ionisé de la matière, tout ce qui est ionisé ne peut pas être appelé plasma.

Plus rigoureusement, le plasma peut être défini comme suit :

Un plasma est un gaz quasi-neutre de particules chargées et neutres qui présente un comportement collectif.
A plasma is a quasineutral gas of charged and neutral particles which exhibits collective behavior.

par Francis F. Chen

Nous verrons ce que signifie la “quasi-neutralité” (quasineutrality) lorsque nous aborderons l’écrantage de Debye (Debye shielding) plus tard. Ici, examinons ce que signifie le “comportement collectif” (collective behavior) du plasma.

Comportement collectif du plasma

Dans le cas d’un gaz non ionisé composé de particules neutres, chaque molécule de gaz est électriquement neutre, donc la force électromagnétique nette agissant sur elle est nulle, et l’effet de la gravité peut également être négligé. Les molécules se déplacent sans être perturbées jusqu’à ce qu’elles entrent en collision avec d’autres molécules, et ces collisions déterminent le mouvement des particules. Même si certaines particules sont ionisées et portent une charge, comme la proportion de particules ionisées dans l’ensemble du gaz est très faible, l’influence électrique de ces particules chargées s’atténue en $1/r^2$ avec la distance et ne s’étend pas très loin.

Cependant, dans un plasma contenant de nombreuses particules chargées, la situation est complètement différente. Le mouvement des particules chargées peut créer des concentrations locales de charges positives ou négatives, générant ainsi des champs électriques. De plus, le mouvement des charges crée des courants, qui à leur tour créent des champs magnétiques. Ces champs électriques et magnétiques peuvent influencer d’autres particules même à grande distance, sans nécessiter de collisions entre particules.

Examinons comment l’intensité de la force électrique agissant entre deux régions de plasma légèrement chargées A et B varie en fonction de la distance r. La force électrique (force de Coulomb) entre A et B diminue en $1/r^2$ à mesure que la distance augmente, conformément à la loi de Coulomb. Cependant, pour un angle solide donné ($\Delta r/r$), le volume de la région de plasma B pouvant influencer A augmente en $r^3$. Par conséquent, les parties constituantes du plasma peuvent exercer des forces significatives les unes sur les autres même à grande distance. Ces forces électriques agissant à longue distance permettent au plasma de présenter une grande variété de comportements dynamiques, et c’est aussi la raison pour laquelle la physique des plasmas existe en tant que discipline scientifique indépendante. Le “comportement collectif” signifie que le mouvement d'une région donnée est influencé non seulement par les conditions locales dans cette région, mais aussi par l'état du plasma dans des régions éloignées.

Équation de Saha

L’équation de Saha est une relation entre l’état d’ionisation, la température et la pression d’un gaz en équilibre thermique, conçue par l’astrophysicien indien Meghnad Saha.

\[\frac{n_{i+1}n_e}{n_i} = \frac{2}{\lambda_{\text{th}}^3}\frac{g_{i+1}}{g_i}\exp{\left[-\frac{\epsilon_{i+1}-\epsilon_i}{k_B T}\right]} \label{eqn:saha_eqn}\tag{1}\]

• $n_i$ : densité des ions positifs de charge $i$ (ayant perdu $i$ électrons)
• $g_i$ : dégénérescence de l’état de l’ion positif de charge $i$
• $\epsilon_i$ : énergie nécessaire pour arracher $i$ électrons à un atome neutre et créer un ion positif de charge $i$
  • $\epsilon_{i+1}-\epsilon_i$ : énergie d’ionisation de l’ordre $(i+1)$
• $n_e$ : densité électronique
• $k_B$ : constante de Boltzmann
• $\lambda_{\text{th}}$ : longueur d’onde thermique de de Broglie (longueur d’onde de de Broglie moyenne des électrons dans le gaz à la température donnée)

\[\lambda_{\text{th}} \equiv \frac{h}{\sqrt{2\pi m_e k_B T}} \quad \text{ (}h\text{: constante de Planck)} \label{eqn:lambda_th}\tag{2}\]

• $m_e$ : masse de l’électron
• $T$ : température du gaz

Si un seul niveau d’ionisation est important et que la production d’ions positifs de charge supérieure à 1 peut être négligée, on peut simplifier en posant $n_1=n_i=n_e$, $n_0=n_n$, $U_i = \epsilon = \epsilon_1$, $i=0$ :

\[\begin{align*} \frac{n_i^2}{n_n} &= \frac{2}{\lambda_{th}^3}\frac{g_1}{g_0}\exp{\left[-\frac{\epsilon}{k_B T} \right]} \label{eqn:saha_eqn_approx}\tag{3}\\ &= 2\left(\frac{2\pi m_e k_B T}{h^2}\right)^{3/2}\frac{g_1}{g_0}e^{-U_i/{k_B T}} \\ &= 2\frac{g_1}{g_0}\left(\frac{2\pi m_e k_B}{h^2}\right)^{3/2}T^{3/2}e^{-U_i/{k_B T}}. \label{eqn:saha_eqn_approx_2}\tag{4} \end{align*}\]

Taux d’ionisation de l’air (azote) à température et pression ambiantes

Dans l’équation ci-dessus, la valeur de $2 \cfrac{g_1}{g_0}$ varie selon le composant du gaz, mais dans de nombreux cas, l’ordre de grandeur de cette valeur est de $1$. On peut donc approximer grossièrement comme suit :

\[\frac{n_i^2}{n_n} \approx \left(\frac{2\pi m_e k_B}{h^2}\right)^{3/2} T^{3/2} e^{-U_i/{k_B T}}.\]

Dans le système SI, les valeurs des constantes fondamentales $m_e$, $k_B$, $h$ sont respectivement :

• $m_e \approx 9,11 \times 10^{-31} \mathrm{kg}$
• $k_B \approx 1,38 \times 10^{-23} \mathrm{J/K}$
• $h \approx 6,63 \times 10^{-34} \mathrm{J \cdot s}$

En les substituant dans l’équation ci-dessus, on obtient :

\[\frac{n_i^2}{n_n} \approx 2,4 \times 10^{21}\ T^{3/2} e^{-U_i/{k_B T}}. \label{eqn:fractional_ionization}\tag{5}\]

À partir de cela, si on calcule la valeur approximative du taux d’ionisation $n_i/(n_n + n_i) \approx n_i/n_n$ pour l’azote ($U_i \approx 14,5\mathrm{eV} \approx 2,32 \times 10^{-18}\mathrm{J}$) dans des conditions de température et de pression ambiantes ($n_n \approx 3 \times 10^{25} \mathrm{m^{-3}}$, $T\approx 300\mathrm{K}$), on obtient :

\[\frac{n_i}{n_n} \approx 10^{-122}\]

Ce qui montre un taux extrêmement faible. C’est la raison pour laquelle, contrairement à l’environnement spatial, on ne rencontre presque jamais de plasma naturellement dans l’atmosphère près de la surface terrestre et du niveau de la mer.

Concept de température en physique des plasmas

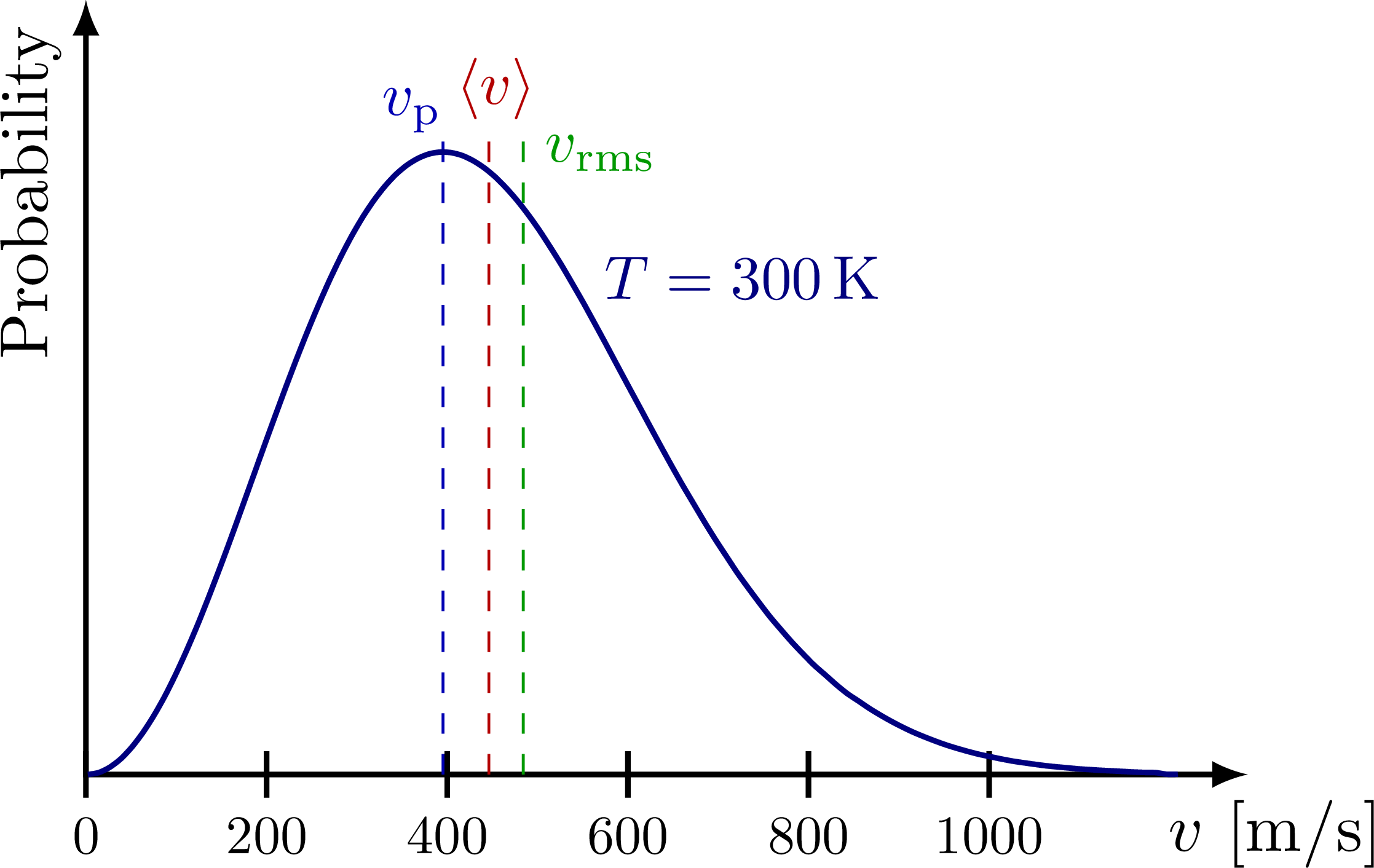
La vitesse des particules constituant un gaz en équilibre thermique suit généralement la distribution de Maxwell-Boltzmann suivante :

\[f(v) = \left(\frac{m}{2\pi k_B T} \right)^{3/2} 4\pi v^2 \exp{\left(-\frac{mv^2}{2k_B T} \right)} \label{eqn:maxwell_boltzmann_dist}\tag{6}\]

Source de l’image

• Auteur : TikZ.net author Izaak Neutelings
• Licence : CC BY-SA 4.0

• Vitesse la plus probable (most probable speed) : $v_p = \sqrt{\cfrac{2k_B T}{m}}$
• Vitesse moyenne (mean speed) : $\langle v \rangle = \sqrt{\cfrac{8k_B T}{\pi m}}$
• Vitesse quadratique moyenne (RMS speed) : $v_{rms} = \sqrt{\langle v^2 \rangle} = \sqrt{\cfrac{3k_B T}{m}}$

L’énergie cinétique moyenne par particule à la température $T$ est $\cfrac{1}{2}m\langle v^2 \rangle = \cfrac{1}{2}mv_{rms}^2 = \cfrac{3}{2}k_B T$ (pour 3 degrés de liberté), déterminée uniquement par la température. Ainsi, dans les gaz et les plasmas, l’énergie cinétique moyenne par particule est étroitement liée à la température, et ces deux grandeurs sont interchangeables. C’est pourquoi il est d’usage en physique des plasmas d’exprimer la température en $\mathrm{eV}$, une unité d’énergie. Pour éviter toute confusion sur les dimensions, on utilise la valeur de $kT$ plutôt que l’énergie cinétique moyenne $\langle E_k \rangle$ pour représenter la température.

La température $T$ correspondant à $kT=1\mathrm{eV}$ est :

\[\begin{align*} T\mathrm{[K]} &= \frac{1,6 \times 10^{-19}\mathrm{[J]}}{1,38 \times 10^{-23}\mathrm{[J/K]}} \\ &= 11600\mathrm{[K]} \end{align*} \label{eqn:temp_conv_factor}\tag{7}\]

Donc, en physique des plasmas, lorsqu’on exprime la température, $1\mathrm{eV}=11600\mathrm{K}$.
Ex : Pour un plasma à une température de $2\mathrm{eV}$, la valeur de $kT$ est $2\mathrm{eV}$, et l’énergie cinétique moyenne par particule est $\cfrac{3}{2}kT=3\mathrm{eV}$.

De plus, un plasma peut avoir simultanément plusieurs températures. Dans un plasma, la fréquence des collisions ion-ion ou électron-électron est plus élevée que celle des collisions électron-ion, ce qui permet aux électrons et aux ions d’atteindre l’équilibre thermique à des températures différentes (température électronique $T_e$ et température ionique $T_i$) et de former des distributions de Maxwell-Boltzmann distinctes. Dans certains cas, la température électronique et la température ionique peuvent être très différentes. De plus, si un champ magnétique externe $\vec{B}$ est appliqué, même pour des particules de même type (par exemple, des ions), l’intensité de la force de Lorentz qu’elles subissent peut varier selon que leur mouvement est parallèle ou perpendiculaire au champ magnétique, ce qui peut entraîner des températures différentes $T_\perp$ et $T_\parallel$.

Relation entre température, pression et densité

Selon la loi des gaz parfaits :

\[PV = \left(\frac{N}{N_A}\right)RT = NkT \label{eqn:ideal_gas_law}\tag{8}\]

D’où :

\[\begin{gather*} P = \frac{NkT}{V} = nkT, \\ n = \frac{P}{kT} \end{gather*} \label{eqn:relation_between_T_P_n}\tag{9}\]

Ainsi, la densité du plasma est inversement proportionnelle à la température ($kT$) et proportionnelle à la pression ($P$).

Classification des plasmas : Plasma froid vs. Plasma chaud

Plasma froid non thermique basse température	Plasma froid thermique basse température	Plasma chaud haute température
$T_i \approx T \approx 300 \mathrm{K}$ $T_i \ll T_e \leqslant 10^5 \mathrm{K}$	$T_i \approx T_e \approx T < 2 \times 10^4 \mathrm{K}$	$T_i \approx T_e > 10^6 \mathrm{K}$
Basse pression ($\sim 100\mathrm{Pa}$) décharge luminescente et arc	Arcs à $100\mathrm{kPa}$ ($1\mathrm{atm}$)	Plasma cinétique, plasma de fusion

Température du plasma

En désignant la température électronique par $T_e$, la température ionique par $T_i$, et la température des particules neutres par $T_g$ :

• Plasma froid : $T_e \mathrm{(>10,000 K)} \gg T_i \approx T_g \mathrm{(\sim 100 K)}$ $\rightarrow$ Plasma hors équilibre (non-equilibrium plasma)
• Plasma (thermique) chaud : $T_e \approx T_i \approx T_g \mathrm{(>10,000 K)}$ $\rightarrow$ Plasma en équilibre (equilibrium plasma)

Densité du plasma

En désignant la densité électronique par $n_e$, la densité ionique par $n_i$, et la densité des particules neutres par $n_g$ :

• Plasma froid : $n_g \gg n_i \approx n_e$ $\rightarrow$ Faible taux d’ionisation, majoritairement composé de particules neutres
• Plasma (thermique) chaud : $n_g \approx n_i \approx n_e $ $\rightarrow$ Taux d’ionisation élevé

Capacité thermique du plasma (À quel point est-il chaud ?)

• Plasma froid : Bien que la température électronique soit élevée, la densité est faible et la majorité des particules sont neutres à température relativement basse, donc la capacité thermique est faible et le plasma n’est pas chaud
• Plasma (thermique) chaud : Les électrons, les ions et les particules neutres sont tous à haute température, donc la capacité thermique est élevée et le plasma est chaud