Rayons X continus et caractéristiques (Continuous and Characteristic X Rays)

TL;DR

• bremsstrahlung (rayonnement de freinage, breaking radiation) : rayons X à spectre continu émis lorsque des particules chargées comme les électrons passent près d’un noyau atomique et sont accélérées par les forces électriques
• Longueur d’onde minimale : $\lambda_\text{min} = \cfrac{hc}{E_\text{max}} = \cfrac{12400 \text{[Å}\cdot\text{eV]}}{V\text{[eV]}}$
• rayons X caractéristiques (characteristic X-ray) : rayons X à spectre discontinu émis lorsqu’un électron incident ionise un électron d’une couche interne de l’atome, et qu’un électron d’une couche externe comble la lacune en émettant un photon d’énergie égale à la différence entre les deux niveaux d’énergie

Prerequisites

• Les particules subatomiques et les constituants de l’atome

Découverte des rayons X

Röntgen a découvert que des rayons X étaient produits lorsqu’un faisceau d’électrons était dirigé vers une cible. Comme on ne savait pas à l’époque que les rayons X étaient des ondes électromagnétiques, ils ont été nommés rayons X (X-ray) en raison de leur nature inconnue, et sont également appelés rayonnement de Röntgen (Röntgen radiation) d’après leur découvreur.

L’image ci-dessus montre la structure simplifiée d’un tube à rayons X typique. À l’intérieur du tube à rayons X sous vide, se trouvent une cathode composée d’un filament de tungstène et une anode sur laquelle est fixée la cible. Lorsqu’une haute tension de plusieurs dizaines de kV est appliquée entre les électrodes, des électrons sont émis par la cathode et dirigés vers la cible de l’anode, produisant ainsi des rayons X. Cependant, l’efficacité de conversion en rayons X est généralement inférieure à 1%, et plus de 99% de l’énergie est convertie en chaleur, nécessitant donc un dispositif de refroidissement supplémentaire.

bremsstrahlung (rayonnement de freinage, braking radiation)

Lorsqu’une particule chargée comme un électron passe près d’un noyau atomique, elle est déviée et ralentie par les forces électriques entre la particule et le noyau, libérant de l’énergie sous forme de rayons X. Cette conversion d’énergie n’étant pas quantifiée, les rayons X émis présentent un spectre continu. Ce phénomène est appelé bremsstrahlung ou rayonnement de freinage (braking radiation).

Cependant, l’énergie des photons X émis par bremsstrahlung ne peut évidemment pas dépasser l’énergie cinétique de l’électron incident. Il existe donc une longueur d’onde minimale pour les rayons X émis, qui peut être calculée simplement par la formule suivante :

\[\lambda_\text{min} = \frac{hc}{E}. \tag{1}\]

La constante de Planck $h$ et la vitesse de la lumière $c$ étant des constantes, cette longueur d’onde minimale n’est déterminée que par l’énergie des électrons incidents. La longueur d’onde $\lambda$ correspondant à une énergie de $1\text{eV}$ est d’environ $1.24 \mu\text{m}=12400\text{Å}$. Ainsi, la longueur d’onde minimale $\lambda_\text{min}$ lorsqu’une tension de $V$ volts est appliquée au tube à rayons X est donnée par la formule suivante, qui est couramment utilisée en pratique :

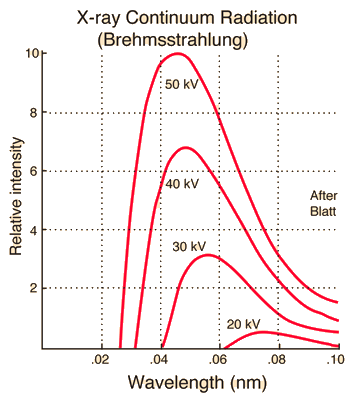
\[\lambda_\text{min} \text{[Å]} = \frac{12400 \text{[Å}\cdot\text{eV]}}{V\text{[eV]}}. \label{eqn:lambda_min}\tag{2}\]

Le graphique suivant montre les spectres continus de rayons X obtenus en faisant varier la tension tout en maintenant constant le courant dans le tube à rayons X. On peut observer que lorsque la tension augmente, la longueur d’onde minimale $\lambda_{\text{min}}$ diminue et l’intensité globale des rayons X augmente.

Rayons X caractéristiques (characteristic X-ray)

Si la tension appliquée au tube à rayons X est suffisamment élevée, l’électron incident peut entrer en collision avec un électron d’une couche interne de l’atome cible et l’ioniser. Dans ce cas, un électron d’une couche externe comble rapidement la lacune de la couche interne en émettant de l’énergie, produisant un photon X dont l’énergie est égale à la différence entre les deux niveaux d’énergie. Le spectre des rayons X émis par ce processus est discontinu et est déterminé par les niveaux d’énergie propres à l’atome cible, indépendamment de l’énergie ou de l’intensité du faisceau d’électrons incident. Ces rayons X sont appelés rayons X caractéristiques (characteristic X-ray).

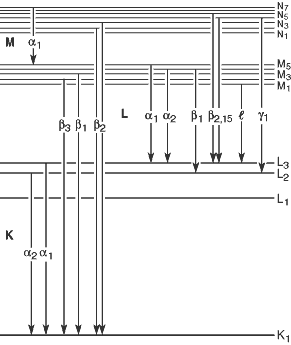
Notation de Siegbahn

Source de l’image

• Auteur : utilisateur Wikipedia anglophone HenrikMidtiby
• Licence : CC BY-SA 3.0

Selon la notation de Siegbahn, les rayons X émis lorsque les électrons des couches L, M, … comblent une lacune dans la couche K sont désignés comme $K_\alpha$, $K_\beta$, … comme montré dans l’image ci-dessus. Cependant, après l’introduction de la notation de Siegbahn et l’émergence du modèle atomique moderne, on a découvert que pour les atomes polyélectroniques, les niveaux d’énergie au sein de chaque couche (niveaux d’énergie ayant le même nombre quantique principal) varient également en fonction d’autres nombres quantiques. Par conséquent, chaque $K_\alpha$, $K_\beta$, … a été subdivisé en $K_{\alpha_1}$, $K_{\alpha_2}$, …

Cette notation traditionnelle est encore largement utilisée en spectroscopie. Cependant, en raison de son manque de systématisation et des confusions qu’elle peut parfois engendrer, l’Union internationale de chimie pure et appliquée (IUPAC) recommande l’utilisation d’une notation différente.

Notation IUPAC

Voici la notation standard recommandée par l’IUPAC pour les orbitales atomiques et les rayons X caractéristiques. Tout d’abord, les noms sont attribués à chaque orbitale atomique selon le tableau suivant :

$n$(nombre quantique principal)	$l$(nombre quantique orbital)	$s$(nombre quantique de spin)	$j$(nombre quantique de moment angulaire total)	Orbitale atomique	Notation X
$1$	$0$	$\pm1/2$	$1/2$	$1s_{1/2}$	$K_{(1)}$
$2$	$0$	$\pm1/2$	$1/2$	$2s_{1/2}$	$L_1$
$2$	$1$	$-1/2$	$1/2$	$2p_{1/2}$	$L_2$
$2$	$1$	$+1/2$	$3/2$	$2p_{3/2}$	$L_3$
$3$	$0$	$\pm1/2$	$1/2$	$3s_{1/2}$	$M_1$
$3$	$1$	$-1/2$	$1/2$	$3p_{1/2}$	$M_2$
$3$	$1$	$+1/2$	$3/2$	$3p_{3/2}$	$M_3$
$3$	$2$	$-1/2$	$3/2$	$3d_{3/2}$	$M_4$
$3$	$2$	$+1/2$	$5/2$	$3d_{5/2}$	$M_5$
$4$	$0$	$\pm1/2$	$1/2$	$4s_{1/2}$	$N_1$
$4$	$1$	$-1/2$	$1/2$	$4p_{1/2}$	$N_2$
$4$	$1$	$+1/2$	$3/2$	$4p_{3/2}$	$N_3$
$4$	$2$	$-1/2$	$3/2$	$4d_{3/2}$	$N_4$
$4$	$2$	$+1/2$	$5/2$	$4d_{5/2}$	$N_5$
$4$	$3$	$-1/2$	$5/2$	$4f_{5/2}$	$N_6$
$4$	$3$	$+1/2$	$7/2$	$4f_{7/2}$	$N_7$

Nombre quantique de moment angulaire total $j=|l+s|$.

Les rayons X caractéristiques émis lorsqu’un électron de l’atome transite d’un niveau d’énergie à un niveau inférieur sont désignés selon la règle suivante :

\[\text{(notation X du niveau final)-(notation X du niveau initial)}\]

Par exemple, les rayons X caractéristiques émis lorsqu’un électron de l’orbitale $2p_{1/2}$ transite vers $1s_{1/2}$ sont appelés $\text{K-L}_2$.

Spectre des rayons X

L’image ci-dessus montre le spectre des rayons X émis lorsqu’un faisceau d’électrons accéléré à 60kV est dirigé vers une cible de rhodium (Rh). On peut observer une courbe lisse et continue due au bremsstrahlung, avec des rayons X émis uniquement pour des longueurs d’onde supérieures à environ $0.207\text{Å} = 20.7\text{pm}$ selon l’équation ($\ref{eqn:lambda_min}$). Les pics aigus qui apparaissent au milieu du graphique sont dus aux rayons X caractéristiques de la couche K du rhodium. Comme mentionné précédemment, chaque atome cible possède son propre spectre caractéristique de rayons X, donc en analysant les longueurs d’onde des pics observés dans le spectre des rayons X émis lors de l’irradiation d’une cible par un faisceau d’électrons, on peut identifier les éléments constituant la cible.

Bien que des rayons X de plus faible énergie comme $L_\alpha, L_\beta, \dots$ soient également émis en plus de $K_\alpha, K_\beta, \dots$, ils ont une énergie beaucoup plus faible et sont généralement absorbés par le boîtier du tube à rayons X avant d’atteindre le détecteur.