Transferencia de energía por colisión

TL;DR

• La energía total y el momento se conservan durante la colisión
• Los iones que han perdido todos sus electrones y los electrones solo tienen energía cinética
• Los átomos neutros y los iones que han perdido solo algunos electrones tienen energía interna, y pueden ocurrir excitación, desexcitación o ionización según los cambios en la energía potencial
• Clasificación de tipos de colisión según los cambios en la energía cinética antes y después de la colisión:
  • Colisión elástica: la cantidad total de energía cinética antes y después de la colisión permanece constante
  • Colisión inelástica: se pierde energía cinética durante el proceso de colisión
    • Excitación
    • Ionización
  • Colisión superelástica: la energía cinética aumenta durante el proceso de colisión
    • Desexcitación
• Tasa de transferencia de energía por colisión elástica:
  • Tasa de transferencia de energía por colisión individual: $\zeta_L = \cfrac{4m_1m_2}{(m_1+m_2)^2}\cos^2\theta_2$
  • Tasa promedio de transferencia de energía por colisión: $\overline{\zeta_L} = \cfrac{4m_1m_2}{(m_1+m_2)^2}\overline{\cos^2\theta_2} = \cfrac{2m_1m_2}{(m_1+m_2)^2}$
    • Cuando $m_1 \approx m_2$: $\overline{\zeta_L} \approx \cfrac{1}{2}$, ocurre una transferencia de energía efectiva y se alcanza rápidamente el equilibrio térmico
    • Cuando $m_1 \ll m_2$ o $m_1 \gg m_2$: $\overline{\zeta_L} \approx 10^{-5}\sim 10^{-4}$, la eficiencia de transferencia de energía es muy baja y es difícil alcanzar el equilibrio térmico. Esta es la razón por la que en plasmas débilmente ionizados, $T_e \gg T_i \approx T_n$, donde la temperatura de los electrones es muy diferente de la temperatura de los iones y átomos neutros.
• Tasa de transferencia de energía por colisión inelástica:
  • Tasa máxima de conversión de energía interna por colisión única: $\zeta_L = \cfrac{\Delta U_\text{max}}{\cfrac{1}{2}m_1v_1^2} = \cfrac{m_2}{m_1+m_2}\cos^2\theta_2$
  • Tasa promedio máxima de conversión de energía interna: $\overline{\zeta_L} = \cfrac{m_2}{m_1+m_2}\overline{\cos^2\theta_2} = \cfrac{m_2}{2(m_1+m_2)}$
    • Cuando $m_1 \approx m_2$: $\overline{\zeta_L} \approx \cfrac{1}{4}$
    • Cuando $m_1 \gg m_2$: $\overline{\zeta_L} \approx 10^{-5}\sim 10^{-4}$
    • Cuando $m_1 \ll m_2$: $\overline{\zeta_L} = \cfrac{1}{2}$, siendo la forma más eficiente de aumentar la energía interna del objetivo de colisión (ion o átomo neutro) y llevarlo a un estado excitado. Esta es la razón por la que la ionización (generación de plasma), excitación (emisión de luz) y disociación de moléculas (generación de radicales) por electrones ocurren fácilmente.

Prerrequisitos

• Partículas subatómicas y componentes del átomo

Colisiones entre partículas en el plasma

• La energía total y el momento se conservan durante la colisión
• Los iones que han perdido todos sus electrones y los electrones solo tienen energía cinética
• Los átomos neutros y los iones que han perdido solo algunos electrones tienen energía interna, y pueden ocurrir excitación, desexcitación o ionización según los cambios en la energía potencial
• Clasificación de tipos de colisión según los cambios en la energía cinética antes y después de la colisión:
  • Colisión elástica: la cantidad total de energía cinética antes y después de la colisión permanece constante
  • Colisión inelástica: se pierde energía cinética durante el proceso de colisión
    • Excitación
    • Ionización
  • Colisión superelástica: la energía cinética aumenta durante el proceso de colisión
    • Desexcitación

Transferencia de energía por colisión elástica

Tasa de transferencia de energía por colisión individual

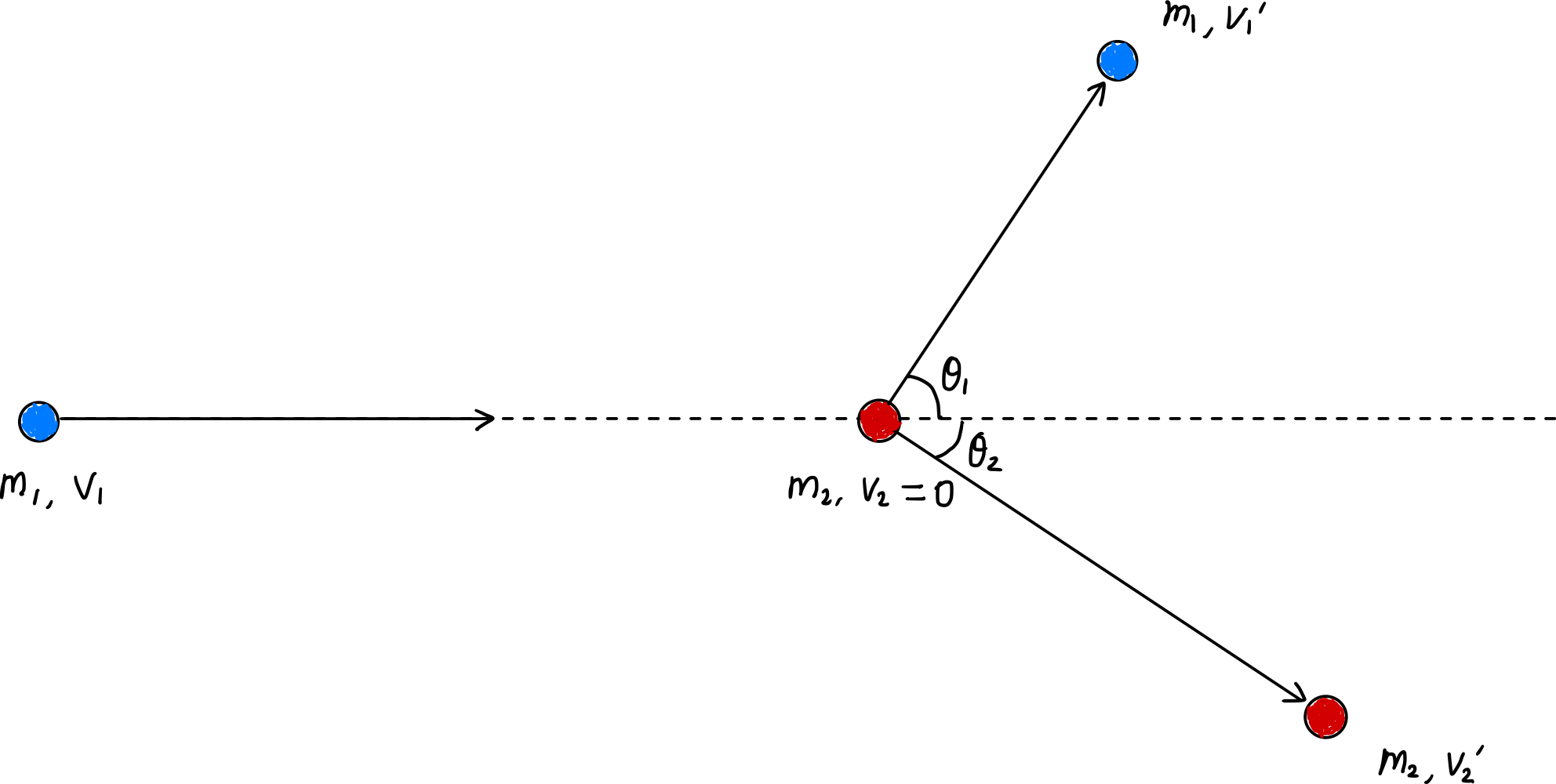
En una colisión elástica, el momento y la energía cinética se conservan antes y después de la colisión.

Estableciendo las ecuaciones de conservación del momento para los ejes $x$ e $y$ respectivamente:

\[\begin{gather*} m_1v_1 = m_1v_1^{\prime}\cos\theta_1 + m_2v_2^{\prime}\cos\theta_2, \label{eqn:momentum_conservation_x}\tag{1} \\ m_1v_1^{\prime}\sin\theta_1 = m_2v_2^{\prime}\sin\theta_2 \label{eqn:momentum_conservation_y}\tag{2} \end{gather*}\]

y por conservación de la energía:

\[\frac{1}{2}m_1v_1^2 = \frac{1}{2}m_1{v_1^{\prime}}^2 + \frac{1}{2}m_2{v_2^{\prime}}^2\] \[v_1^2 = {v_1^{\prime}}^2 + \frac{m_2}{m_1}{v_2^{\prime}}^2 \label{eqn:energy_conservation}\tag{3}\]

De la ecuación ($\ref{eqn:momentum_conservation_x}$):

\[m_1 v_1^{\prime} \cos \theta_1 = m_1v_1 - m_2v_2^{\prime} \cos \theta_2 \label{eqn:momentum_conservation_x_2}\tag{4}\]

y elevando al cuadrado y sumando ambos lados de las ecuaciones ($\ref{eqn:momentum_conservation_y}$) y ($\ref{eqn:momentum_conservation_x_2}$):

\[\begin{align*} (m_1v_1^{\prime})^2 &= (m_2 v_2^\prime \sin \theta_2)^2 + (m_1 v_1 - m_2 v_2^\prime \cos \theta_2)^2 \\ &= m_1^2 v_1^2 - 2 m_1 m_2 v_1 v_2^\prime \cos \theta_2 + m_2^2 {v_2^\prime}^2 \tag{5} \end{align*}\]

Ahora, dividiendo ambos lados por $m_1^2$:

\[{v_1^{\prime}}^2 = v_1^2 - 2 \frac{m_2}{m_1} v_1 v_2^\prime \cos \theta_2 + \left(\frac{m_2}{m_1}\right)^2 {v_2^\prime}^2 \label{eqn:momentum_conservation}\tag{6}\]

Sustituyendo la ecuación ($\ref{eqn:energy_conservation}$) aquí, podemos reorganizar como sigue:

\[\begin{gather*} \left( \frac{m_2}{m_1} \right) {v_2^\prime}^2 = 2 \left( \frac{m_2}{m_1} \right) v_1 v_2^\prime \cos \theta_2 - \left( \frac{m_2}{m_1} \right)^2 {v_2^\prime}^2 \\ 2v_1 \cos \theta_2 = \left(\frac{m_1 + m_2}{m_1} \right) v_2^\prime \\ v_2^{\prime} = \frac{2m_1v_1\cos\theta_2}{m_1 + m_2}. \label{eqn:v_2_prime}\tag{7} \end{gather*}\]

De esto, obtenemos la tasa de transferencia de energía $\zeta_L$ como sigue:

\[\begin{align*} \therefore \zeta_L &= \frac{\cfrac{1}{2}m_2{v_2^\prime}^2}{\cfrac{1}{2}m_1v_1^2} = \frac{m_2}{m_1v_1^2} {\left(\frac{2m_1v_1\cos\theta_2}{m_1 + m_2} \right)}^2 \\ &= \frac{4m_1m_2}{(m_1+m_2)^2}\cos^2\theta_2. \quad \blacksquare \label{eqn:elastic_E_transfer_rate}\tag{8} \end{align*}\]

Tasa promedio de transferencia de energía por colisión

Para ángulos de 0 a 2π, $\sin^2{\theta_2}+\cos^2{\theta_2}=1$ y $\overline{\sin^2{\theta_2}}=\overline{\cos^2{\theta_2}}$, por lo tanto:

\[\begin{align*} \overline{\cos^2{\theta_2}} &= \overline{(1-\sin^2{\theta_2})} = 1 - \overline{\sin^2{\theta_2}} \\ &= 1 - \overline{\cos^2{\theta_2}} \end{align*}\] \[\begin{gather*} 2 \cdot \overline{\cos^2{\theta_2}} = 1 \\ \overline{\cos^2{\theta_2}} = \frac{1}{2}. \end{gather*}\]

Sustituyendo esto en la ecuación ($\ref{eqn:elastic_E_transfer_rate}$) que obtuvimos anteriormente:

\[\overline{\zeta_L} = \frac{4m_1m_2}{(m_1+m_2)^2}\overline{\cos^2\theta_2} = \frac{2m_1m_2}{(m_1+m_2)^2}. \quad \blacksquare \label{eqn:elastic_E_mean_transfer_rate}\tag{9}\]

Cuando $m_1 \approx m_2$

Esto se aplica a colisiones electrón-electrón, ion-ion, átomo neutro-átomo neutro, ion-átomo neutro. En estos casos:

\[\overline{\zeta_L} = \frac{2m_1m_2}{(m_1+m_2)^2} \approx \frac{1}{2} \label{eqn:elastic_similar_m}\tag{10}\]

lo que resulta en una transferencia de energía efectiva y un rápido alcance del equilibrio térmico.

Cuando $m_1 \ll m_2$ o $m_1 \gg m_2$

Esto se aplica a colisiones electrón-ion, electrón-átomo neutro, ion-electrón, átomo neutro-electrón. En estos casos:

\[\overline{\zeta_L} = \frac{2m_1m_2}{(m_1+m_2)^2} \approx \frac{2m_1}{m_2}\text{ (basado en }m_1 \ll m_2 \text{)} \approx 10^{-5}\sim 10^{-4} \label{eqn:elastic_different_m}\tag{11}\]

lo que resulta en una eficiencia de transferencia de energía muy baja, dificultando el alcance del equilibrio térmico. Esta es la razón por la que en plasmas débilmente ionizados, $T_e \gg T_i \approx T_n$, donde la temperatura de los electrones es muy diferente de la temperatura de los iones y átomos neutros.

Transferencia de energía por colisión inelástica

Tasa máxima de conversión de energía interna por colisión única

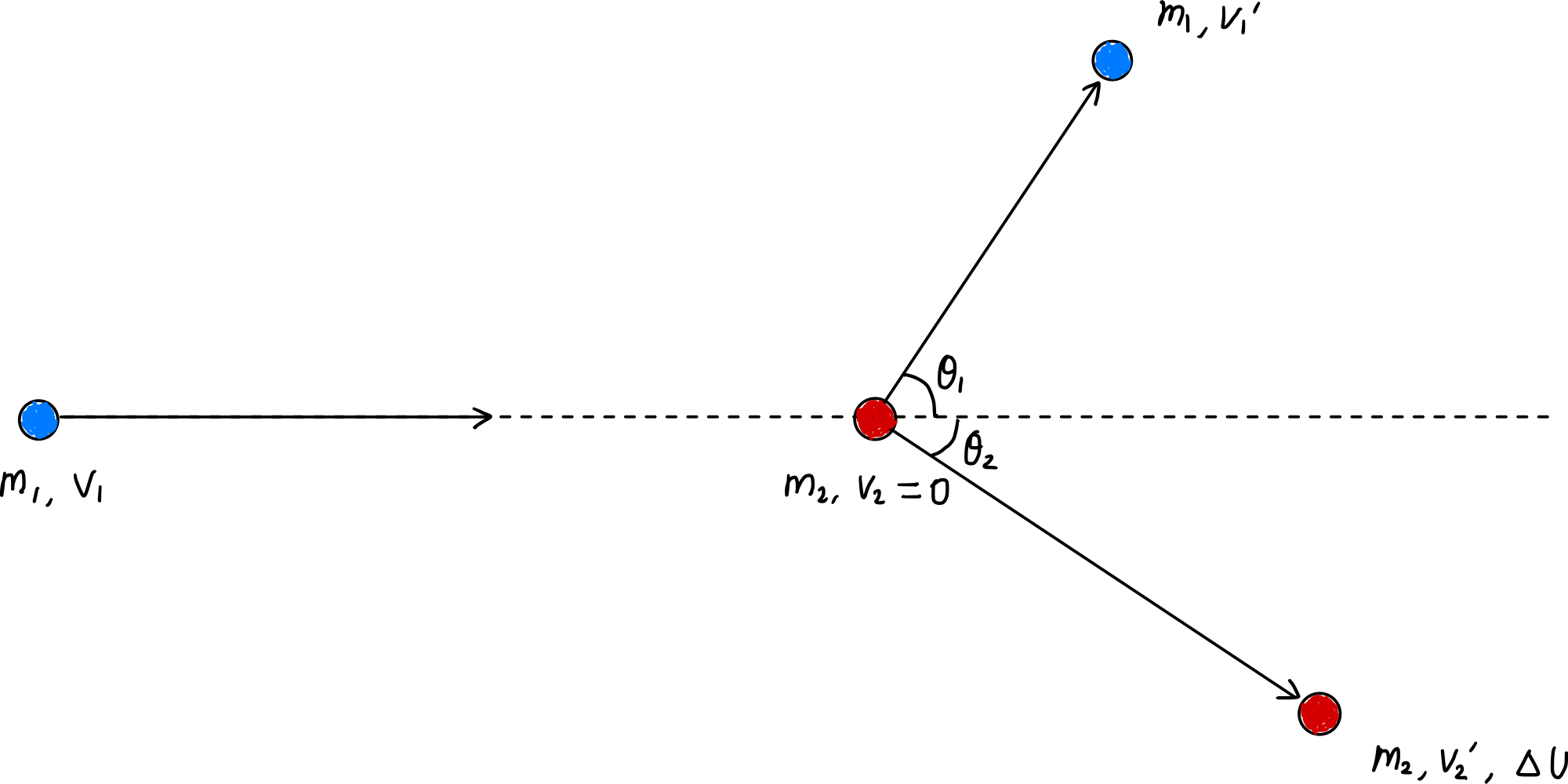
La conservación del momento (ecuación [$\ref{eqn:momentum_conservation}$]) se mantiene igual en este caso, pero como es una colisión inelástica, la energía cinética no se conserva. En este caso, la energía cinética perdida por la colisión inelástica se convierte en energía interna $\Delta U$, por lo tanto:

\[\Delta U = \frac{1}{2} m_1 v_1^2 - \left( \frac{1}{2} m_1 {v_1^{\prime}}^2 + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right) \label{eqn:delta_U}\tag{12}\]

Ahora, sustituyendo la ecuación ($\ref{eqn:momentum_conservation}$) aquí y reorganizando, obtenemos:

\(\begin{align*} \Delta U &= \frac{1}{2} m_1 v_1^2 - \left[ \frac{1}{2} m_1 \left( v_1^2 - 2 \frac{m_2}{m_1} v_1 v_2^{\prime} \cos \theta_2 + \left( \frac{m_2}{m_1} v_2^{\prime} \right)^2 \right) + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right] \\ &= \frac{1}{2} m_1 v_1^2 - \left[ \frac{1}{2} m_1 v_1^2 - m_2 v_1 v_2^{\prime} \cos \theta_2 + \frac{1}{2} \frac{m_2^2}{m_1} {v_2^{\prime}}^2 + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right] \\ &= m_2 v_1 v_2^{\prime} \cos \theta_2 - \frac{1}{2}m_2{v_2^{\prime}}^2\left(\frac{m_1 + m_2}{m_1}\right) \label{eqn:delta_U_2}\tag{13} \end{align*}\).

Diferenciando $\Delta U$ con respecto a $v_2^\prime$, encontrando el punto extremo donde la derivada es 0 y el valor máximo en ese punto:

\[\cfrac{d \Delta U}{d v_2^{\prime}} = m_2 v_1 \cos \theta_2 - m_2 v_2^{\prime} \left( \frac{m_1 + m_2}{m_1} \right) = 0 \tag{14}\] \[\begin{gather*} v_2^{\prime} \left( \frac{m_1 + m_2}{m_1} \right) = v_1 \cos \theta_2 \\ v_2^\prime = \frac{m_1v_1\cos\theta_2}{m_1+m_2}. \end{gather*}\] \[\therefore v_2^{\prime} = \frac{m_1v_1\cos\theta_2}{m_1+m_2} \text{ cuando } \Delta U_\text{max} = \frac{1}{2}\frac{m_1m_2 v_1^2 \cos^2\theta_2}{m_1 + m_2}. \label{eqn:delta_U_max}\tag{15}\]

De esto, la tasa máxima de conversión posible de energía cinética a energía interna por una sola colisión inelástica $\zeta_L$ es:

\[\zeta_L = \frac{\Delta U_\text{max}}{\cfrac{1}{2}m_1v_1^2} = \frac{m_2}{m_1+m_2}\cos^2\theta_2. \quad \blacksquare \label{eqn:inelastic_E_transfer_rate}\tag{16}\]

Tasa promedio máxima de conversión de energía interna

De manera similar, sustituyendo $\overline{\cos^2{\theta_2}} = \cfrac{1}{2}$ en la ecuación ($\ref{eqn:inelastic_E_transfer_rate}$), obtenemos:

\[\overline{\zeta_L} = \frac{m_2}{m_1+m_2}\overline{\cos^2\theta_2} = \frac{m_2}{2(m_1+m_2)}. \label{eqn:inelastic_E_mean_transfer_rate}\tag{17}\]

Cuando $m_1 \approx m_2$

Esto se aplica a colisiones ion-ion, ion-átomo neutro, átomo neutro-átomo neutro.

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} = \frac{1}{4}. \label{eqn:inelastic_similar_m}\tag{18}\]

Cuando $m_1 \gg m_2$

Esto se aplica a colisiones ion-electrón, átomo neutro-electrón.

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} \approx \frac{m_2}{2m_1} \approx 10^{-5}\sim 10^{-4}. \label{eqn:inelastic_ion_electron}\tag{19}\]

Cuando $m_1 \ll m_2$

Esto se aplica a colisiones electrón-ion, electrón-átomo neutro. Mientras que los dos casos anteriores no mostraron una diferencia significativa con respecto a las colisiones elásticas, este tercer caso muestra una diferencia importante. En este caso:

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} \approx \frac{m_2}{2m_2} = \frac{1}{2} \label{eqn:inelastic_electron_ion}\tag{20}\]

lo que resulta en la forma más eficiente de aumentar la energía interna del objetivo de colisión (ion o átomo neutro) y llevarlo a un estado excitado. Como veremos más adelante, esta es la razón por la que la ionización por electrones (generación de plasma), excitación (emisión de luz) y disociación de moléculas (generación de radicales) ocurren fácilmente.