Definición de plasma, concepto de temperatura y la ecuación de Saha

TL;DR

• Plasma: Gas cuasineutro de partículas cargadas y neutras que exhibe comportamiento colectivo
• ‘Comportamiento colectivo’ del plasma:
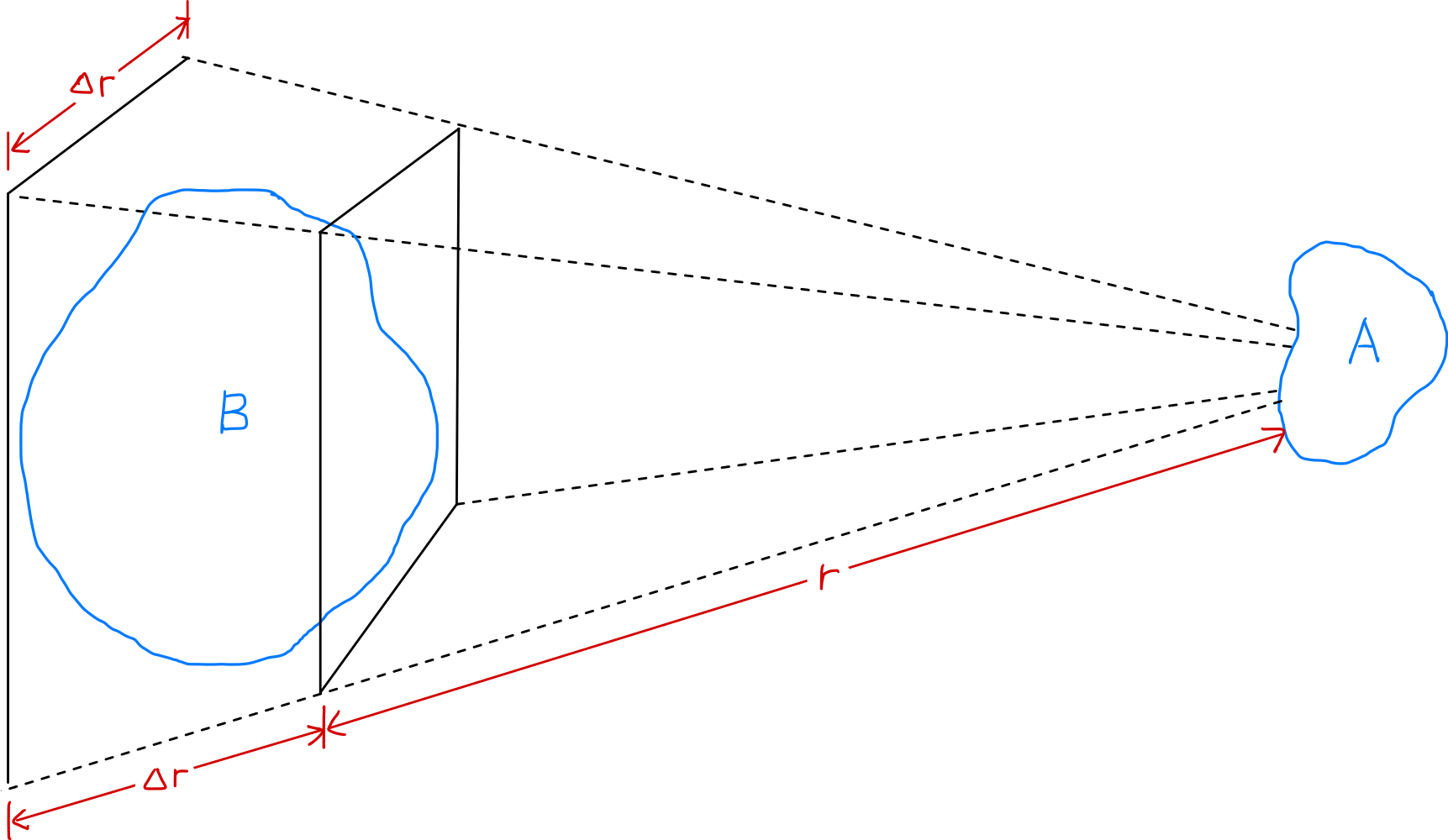
  • La fuerza eléctrica entre dos regiones A y B del plasma disminuye con $1/r^2$ al aumentar la distancia
  • Sin embargo, el volumen de la región B del plasma que puede influir en A aumenta con $r^3$ para un ángulo sólido dado ($\Delta r/r$)
  • Por lo tanto, las partes que componen el plasma pueden ejercer fuerzas significativas entre sí incluso a largas distancias
• Ecuación de Saha: Relación entre el estado de ionización, temperatura y presión de un gas en equilibrio térmico

\[\frac{n_{i+1}n_e}{n_i} = \frac{2}{\lambda_{\text{th}}^3}\frac{g_{i+1}}{g_i}\exp{\left[-\frac{\epsilon_{i+1}-\epsilon_i}{k_B T}\right]}\]

• Concepto de temperatura en física del plasma:
  • La energía cinética media por partícula en gases y plasmas está estrechamente relacionada con la temperatura, y ambas son cantidades físicas intercambiables
  • En física del plasma, es convencional expresar la temperatura en unidades de energía $\mathrm{eV}$ como el valor de $kT$
    • $1\mathrm{eV}=11600\mathrm{K}$
  • El plasma puede tener simultáneamente varias temperaturas diferentes, en particular la temperatura de los electrones ($T_e$) y la temperatura de los iones ($T_i$) pueden ser muy diferentes en algunos casos
• Plasma frío vs. plasma caliente:
  • Temperatura del plasma:
    • Plasma frío: $T_e \text{(>10,000℃)} \gg T_i \approx T_g \text{(}\sim\text{100℃)}$ $\rightarrow$ Plasma no equilibrado (non-equilibrium plasma)
    • Plasma caliente (térmico): $T_e \approx T_i \approx T_g \text{(>10,000℃)}$ $\rightarrow$ Plasma en equilibrio (equilibrium plasma)
  • Densidad del plasma:
    • Plasma frío: $n_g \gg n_i \approx n_e$ $\rightarrow$ Baja tasa de ionización, mayormente partículas neutras
    • Plasma caliente (térmico): $n_g \approx n_i \approx n_e $ $\rightarrow$ Alta tasa de ionización
  • Capacidad calorífica del plasma:
    • Plasma frío: Alta temperatura de electrones pero baja densidad, mayormente partículas neutras a baja temperatura, por lo que tiene baja capacidad calorífica y no está caliente
    • Plasma caliente (térmico): Electrones, iones y partículas neutras a alta temperatura, por lo que tiene alta capacidad calorífica y está caliente

Prerrequisitos

• Partículas subatómicas y componentes del átomo
• Distribución de Maxwell-Boltzmann (mecánica estadística)
• Masa y energía, partículas y ondas
• Simetría y leyes de conservación (mecánica cuántica), degeneración

Definición de plasma

Normalmente, en textos dirigidos a no especialistas, el plasma se define de la siguiente manera:

El cuarto estado de la materia, después de sólido, líquido y gaseoso, obtenido al calentar un gas hasta un estado de ultra-alta temperatura donde los átomos constituyentes se separan en electrones e iones positivos hasta ionizarse

Esto no es incorrecto, y de hecho el sitio web del Instituto Coreano de Energía de Fusión (Korea Institute of Fusion Energy) lo presenta de manera similar. Es también la definición popular que uno encuentra fácilmente al buscar sobre plasma.

Sin embargo, aunque esta expresión es ciertamente correcta, no puede considerarse una definición rigurosa. Los gases a temperatura y presión ambiente también están ionizados en una proporción extremadamente pequeña, pero no los llamamos plasma. Cuando se disuelve una sustancia de enlace iónico como el cloruro de sodio en agua, se separa en iones cargados, pero esta solución tampoco es un plasma.
Es decir, aunque el plasma es un estado ionizado de la materia, no todo lo que está ionizado es plasma.

De manera más rigurosa, el plasma se puede definir como:

Un plasma es un gas cuasineutro de partículas cargadas y neutras que exhibe comportamiento colectivo.
A plasma is a quasineutral gas of charged and neutral particles which exhibits collective behavior.

por Francis F. Chen

Veremos qué significa ‘cuasineutralidad (quasineutrality)’ cuando tratemos el apantallamiento de Debye (Debye shielding) más adelante. Aquí, veamos qué significa el ‘comportamiento colectivo (collective behavior)’ del plasma.

Comportamiento colectivo del plasma

En el caso de un gas no ionizado compuesto de partículas neutras, cada molécula de gas es eléctricamente neutra, por lo que la fuerza electromagnética neta que actúa es $0$, y el efecto de la gravedad también se puede ignorar. Las moléculas se mueven sin obstáculos hasta que colisionan con otras moléculas, y las colisiones entre moléculas determinan el movimiento de las partículas. Incluso si algunas partículas se ionizan y adquieren carga, la proporción de partículas ionizadas en el gas total es muy baja, por lo que la influencia eléctrica de estas partículas cargadas se atenúa con $1/r^2$ según la distancia y no alcanza largas distancias.

Sin embargo, en un plasma que contiene muchas partículas cargadas, la situación es completamente diferente. El movimiento de las partículas cargadas puede causar concentraciones locales de carga positiva o negativa, lo que genera campos eléctricos. Además, el movimiento de cargas crea corrientes, y las corrientes generan campos magnéticos. Estos campos eléctricos y magnéticos pueden afectar a otras partículas distantes sin necesidad de colisiones entre partículas.

Veamos cómo varía la intensidad de la fuerza eléctrica entre dos regiones de plasma ligeramente cargadas $A$ y $B$ con la distancia $r$. La fuerza eléctrica (fuerza de Coulomb) entre $A$ y $B$ disminuye con $1/r^2$ al aumentar la distancia. Sin embargo, para un ángulo sólido dado ($\Delta r/r$), el volumen de la región de plasma $B$ que puede influir en $A$ aumenta con $r^3$. Por lo tanto, las partes que componen el plasma pueden ejercer fuerzas significativas entre sí incluso a largas distancias. Esta fuerza eléctrica de largo alcance permite que el plasma exhiba una gran variedad de patrones de movimiento, y es también la razón por la que existe la física del plasma (plasma physics) como un campo de estudio independiente. El ‘comportamiento colectivo (collective behavior)’ significa que el movimiento de una región está influenciado no solo por las condiciones locales en esa región, sino también por el estado del plasma en regiones distantes.

Ecuación de Saha (Saha equation)

La ecuación de Saha (Saha equation) es una relación entre el estado de ionización, la temperatura y la presión de un gas en equilibrio térmico, concebida por el astrofísico indio Meghnad Saha.

\[\frac{n_{i+1}n_e}{n_i} = \frac{2}{\lambda_{\text{th}}^3}\frac{g_{i+1}}{g_i}\exp{\left[-\frac{\epsilon_{i+1}-\epsilon_i}{k_B T}\right]} \label{eqn:saha_eqn}\tag{1}\]

• $n_i$: densidad de iones positivos $i$ (iones positivos que han perdido $i$ electrones)
• $g_i$: degeneración del estado del ion positivo $i$
• $\epsilon_i$: energía necesaria para separar $i$ electrones de un átomo neutro y crear un ion positivo $i$
  • $\epsilon_{i+1}-\epsilon_i$: energía de ionización de orden $(i+1)$
• $n_e$: densidad de electrones
• $k_B$: constante de Boltzmann
• $\lambda_{\text{th}}$: longitud de onda térmica de De Broglie (longitud de onda de De Broglie promedio de los electrones en el gas a una temperatura dada)

\[\lambda_{\text{th}} \equiv \frac{h}{\sqrt{2\pi m_e k_B T}} \quad \text{ (}h\text{: constante de Planck)} \label{eqn:lambda_th}\tag{2}\]

• $m_e$: masa del electrón
• $T$: temperatura del gas

Si solo es importante un nivel de ionización y se puede ignorar la producción de iones positivos de carga 2 o superior, podemos simplificar poniendo $n_1=n_i=n_e$, $n_0=n_n$, $U_i = \epsilon = \epsilon_1$, $i=0$ de la siguiente manera:

\[\begin{align*} \frac{n_i^2}{n_n} &= \frac{2}{\lambda_{th}^3}\frac{g_1}{g_0}\exp{\left[-\frac{\epsilon}{k_B T} \right]} \label{eqn:saha_eqn_approx}\tag{3}\\ &= 2\left(\frac{2\pi m_e k_B T}{h^2}\right)^{3/2}\frac{g_1}{g_0}e^{-U_i/{k_B T}} \\ &= 2\frac{g_1}{g_0}\left(\frac{2\pi m_e k_B}{h^2}\right)^{3/2}T^{3/2}e^{-U_i/{k_B T}}. \label{eqn:saha_eqn_approx_2}\tag{4} \end{align*}\]

Tasa de ionización del aire (nitrógeno) a temperatura y presión ambiente

En la ecuación anterior, el valor de $2 \cfrac{g_1}{g_0}$ varía según el componente del gas, pero en muchos casos el orden de magnitud de este valor es $1$. Por lo tanto, podemos aproximar de manera general como sigue:

\[\frac{n_i^2}{n_n} \approx \left(\frac{2\pi m_e k_B}{h^2}\right)^{3/2} T^{3/2} e^{-U_i/{k_B T}}.\]

En el sistema SI, los valores de las constantes fundamentales $m_e$, $k_B$, $h$ son respectivamente:

• $m_e \approx 9.11 \times 10^{-31} \mathrm{kg}$
• $k_B \approx 1.38 \times 10^{-23} \mathrm{J/K}$
• $h \approx 6.63 \times 10^{-34} \mathrm{J \cdot s}$

Sustituyendo estos en la ecuación anterior, obtenemos:

\[\frac{n_i^2}{n_n} \approx 2.4 \times 10^{21}\ T^{3/2} e^{-U_i/{k_B T}}. \label{eqn:fractional_ionization}\tag{5}\]

A partir de esto, si calculamos el valor aproximado de la tasa de ionización $n_i/(n_n + n_i) \approx n_i/n_n$ para el nitrógeno ($U_i \approx 14.5\mathrm{eV} \approx 2.32 \times 10^{-18}\mathrm{J}$) en condiciones de temperatura y presión ambiente ($n_n \approx 3 \times 10^{25} \mathrm{m^{-3}}$, $T\approx 300\mathrm{K}$), obtenemos:

\[\frac{n_i}{n_n} \approx 10^{-122}\]

lo que indica una tasa extremadamente baja. Esta es la razón por la que, a diferencia del entorno espacial, casi no encontramos plasma de forma natural en el ambiente atmosférico cerca de la superficie terrestre y el nivel del mar.

Concepto de temperatura en física del plasma

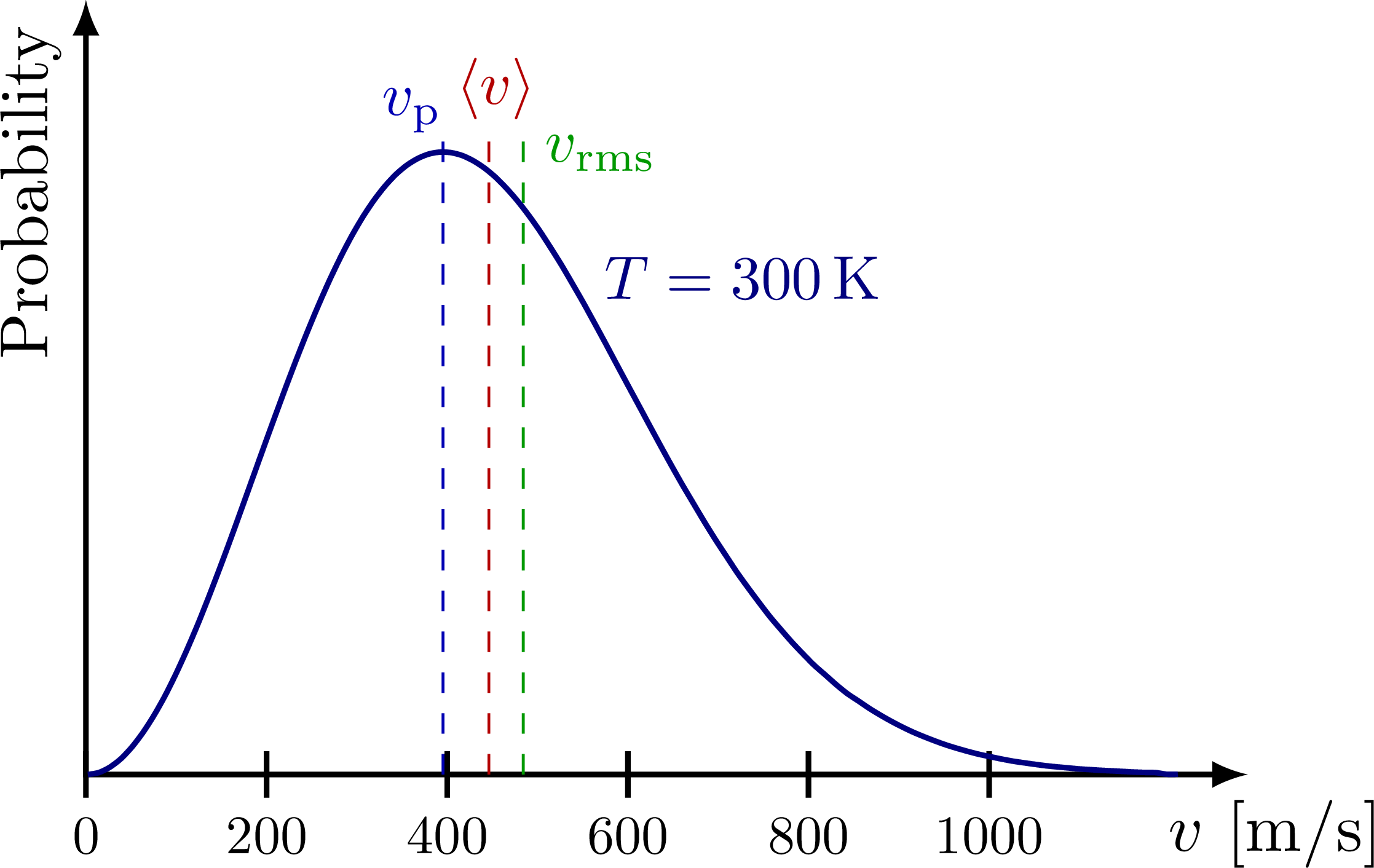
La velocidad de las partículas que componen un gas en equilibrio térmico generalmente sigue la distribución de Maxwell-Boltzmann:

\[f(v) = \left(\frac{m}{2\pi k_B T} \right)^{3/2} 4\pi v^2 \exp{\left(-\frac{mv^2}{2k_B T} \right)} \label{eqn:maxwell_boltzmann_dist}\tag{6}\]

Fuente de la imagen

• Autor: TikZ.net author Izaak Neutelings
• Licencia: CC BY-SA 4.0

• Velocidad más probable (most probable speed): $v_p = \sqrt{\cfrac{2k_B T}{m}}$
• Velocidad media (mean speed): $\langle v \rangle = \sqrt{\cfrac{8k_B T}{\pi m}}$
• Velocidad cuadrática media (RMS speed): $v_{rms} = \sqrt{\langle v^2 \rangle} = \sqrt{\cfrac{3k_B T}{m}}$

La energía cinética media por partícula a temperatura $T$ es $\cfrac{1}{2}m\langle v^2 \rangle = \cfrac{1}{2}mv_{rms}^2 = \cfrac{3}{2}k_B T$ (basado en 3 grados de libertad), determinada solo por la temperatura. Como la energía cinética media por partícula en gases y plasmas está estrechamente relacionada con la temperatura, y estas dos son cantidades físicas intercambiables, en física del plasma es convencional expresar la temperatura en unidades de energía $\mathrm{eV}$. Para evitar confusión con las dimensiones, se expresa la temperatura como el valor de $kT$ en lugar de la energía cinética media $\langle E_k \rangle$.

La temperatura $T$ cuando $kT=1\mathrm{eV}$ es:

\[\begin{align*} T\mathrm{[K]} &= \frac{1.6 \times 10^{-19}\mathrm{[J]}}{1.38 \times 10^{-23}\mathrm{[J/K]}} \\ &= 11600\mathrm{[K]} \end{align*} \label{eqn:temp_conv_factor}\tag{7}\]

Por lo tanto, en física del plasma, cuando se expresa la temperatura, $1\mathrm{eV}=11600\mathrm{K}$.
Ej.) Para un plasma a temperatura de $2\mathrm{eV}$, el valor de $kT$ es $2\mathrm{eV}$, y la energía cinética media por partícula es $\cfrac{3}{2}kT=3\mathrm{eV}$.

Además, el plasma puede tener varias temperaturas simultáneamente. En el plasma, la frecuencia de colisiones entre iones o entre electrones es mayor que la frecuencia de colisiones entre electrones e iones, lo que permite que los electrones y los iones alcancen el equilibrio térmico a diferentes temperaturas (temperatura de electrones $T_e$ y temperatura de iones $T_i$), formando distribuciones de Maxwell-Boltzmann separadas, y en algunos casos la temperatura de los electrones y la temperatura de los iones pueden ser muy diferentes. Incluso, si se aplica un campo magnético externo $\vec{B}$, las partículas del mismo tipo (por ejemplo, iones) pueden tener diferentes temperaturas $T_\perp$ y $T_\parallel$ dependiendo de si su movimiento es paralelo o perpendicular al campo magnético, ya que la intensidad de la fuerza de Lorentz que reciben es diferente.

Relación entre temperatura, presión y densidad

Según la ley de los gases ideales:

\[PV = \left(\frac{N}{N_A}\right)RT = NkT \label{eqn:ideal_gas_law}\tag{8}\]

De esto, obtenemos:

\[\begin{gather*} P = \frac{NkT}{V} = nkT, \\ n = \frac{P}{kT} \end{gather*} \label{eqn:relation_between_T_P_n}\tag{9}\]

Es decir, la densidad del plasma es inversamente proporcional a la temperatura ($kT$) y proporcional a la presión ($P$).

Clasificación del plasma: Plasma frío vs. Plasma caliente

Plasma frío no térmico de baja temperatura	Plasma frío térmico de baja temperatura	Plasma caliente de alta temperatura
$T_i \approx T \approx 300 \mathrm{K}$ $T_i \ll T_e \leqslant 10^5 \mathrm{K}$	$T_i \approx T_e \approx T < 2 \times 10^4 \mathrm{K}$	$T_i \approx T_e > 10^6 \mathrm{K}$
Baja presión($\sim 100\mathrm{Pa}$) descarga luminiscente y arco	Arcos a $100\mathrm{kPa}$ ($1\mathrm{atm}$)	Plasma cinético, plasma de fusión

Temperatura del plasma

Siendo $T_e$ la temperatura de los electrones, $T_i$ la temperatura de los iones y $T_g$ la temperatura de las partículas neutras:

• Plasma frío: $T_e \mathrm{(>10,000 K)} \gg T_i \approx T_g \mathrm{(\sim 100 K)}$ $\rightarrow$ Plasma no equilibrado (non-equilibrium plasma)
• Plasma caliente (térmico): $T_e \approx T_i \approx T_g \mathrm{(>10,000 K)}$ $\rightarrow$ Plasma en equilibrio (equilibrium plasma)

Densidad del plasma

Siendo $n_e$ la densidad de electrones, $n_i$ la densidad de iones y $n_g$ la densidad de partículas neutras:

• Plasma frío: $n_g \gg n_i \approx n_e$ $\rightarrow$ Baja tasa de ionización, mayormente partículas neutras
• Plasma caliente (térmico): $n_g \approx n_i \approx n_e $ $\rightarrow$ Alta tasa de ionización

Capacidad calorífica del plasma (¿Qué tan caliente es?)

• Plasma frío: Alta temperatura de electrones pero baja densidad, mayormente partículas neutras a baja temperatura, por lo que tiene baja capacidad calorífica y no está caliente
• Plasma caliente (térmico): Electrones, iones y partículas neutras a alta temperatura, por lo que tiene alta capacidad calorífica y está caliente