Das freie Teilchen

TL;DR

• Freies Teilchen: $V(x)=0$, keine Randbedingungen (beliebige Energie)
• Die separierte Lösung $\Psi_k(x,t) = Ae^{i\left(kx-\frac{\hbar k^2}{2m}t \right)}$ divergiert bei Quadratintegration gegen unendlich und ist daher nicht normierbar, was folgendes impliziert:
  • Freie Teilchen können nicht als stationäre Zustände existieren
  • Freie Teilchen können keine exakt definierte Energie haben (Energieunschärfe existiert)
• Dennoch hat die separierte Lösung wichtige mathematische Bedeutung, da die allgemeine Lösung der zeitabhängigen Schrödinger-Gleichung eine Linearkombination der separierten Lösungen ist. Da es jedoch keine Beschränkungen gibt, ist die allgemeine Lösung ein Integral über die kontinuierliche Variable $k$ ($\int$) anstatt einer Summe über diskrete Variable $n$ ($\sum$).
• Allgemeine Lösung der Schrödinger-Gleichung:

\[\begin{gather*} \Psi(x,t) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{i(kx-\frac{\hbar k^2}{2m}t)}dk, \\ \text{wobei }\phi(k) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\Psi(x,0)e^{-ikx}dx \end{gather*}\]

• Beziehung zwischen Orts- und Impulsunschärfe:
  • Wenn die Ortsunschärfe abnimmt, nimmt die Impulsunschärfe zu, und umgekehrt
  • Das heißt, quantenmechanisch ist es unmöglich, Ort und Impuls eines freien Teilchens gleichzeitig exakt zu bestimmen
• Phasen- und Gruppengeschwindigkeit der Wellenfunktion $\Psi(x,t)$:
  • Phasengeschwindigkeit: $v_\text{phase} = \cfrac{\omega}{k} = \cfrac{\hbar k}{2m}$
  • Gruppengeschwindigkeit: $v_\text{group} = \cfrac{d\omega}{dk} = \cfrac{\hbar k}{m}$
• Physikalische Bedeutung der Gruppengeschwindigkeit und Vergleich mit der klassischen Mechanik:
  • Physikalisch entspricht die Gruppengeschwindigkeit der Bewegungsgeschwindigkeit des entsprechenden Teilchens
  • Wenn $\phi(k)$ eine sehr scharfe Form um einen Wert $k_0$ herum hat (wenn die Impulsunschärfe ausreichend klein ist),

\[v_\text{group} = v_\text{classical} = \sqrt{\cfrac{2E}{m}}\]

Voraussetzungen

• Eulersche Formel
• Fourier-Transformation & Plancherel-Theorem
• Schrödinger-Gleichung und Wellenfunktion
• Zeitunabhängige Schrödinger-Gleichung
• Der eindimensionale unendliche Potentialtopf

Modellaufstellung

Betrachten wir den einfachsten Fall eines freien Teilchens ($V(x)=0$). Klassisch ist dies nur eine gleichförmige Bewegung, aber in der Quantenmechanik ist dieses Problem interessanter.
Die zeitunabhängige Schrödinger-Gleichung für ein freies Teilchen lautet

\[-\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2}=E\psi \tag{1}\]

also

\[\frac{d^2\psi}{dx^2} = -k^2\psi \text{, wobei }k\equiv \frac{\sqrt{2mE}}{\hbar} \label{eqn:t_independent_schrodinger_eqn}\tag{2}\]

Bis hierhin ist es dasselbe wie im Inneren des unendlichen Potentialtopfs mit Potential $0$. Diesmal schreiben wir jedoch die allgemeine Lösung in der folgenden Exponentialform:

\[\psi(x) = Ae^{ikx} + Be^{-ikx}. \tag{3}\]

$Ae^{ikx} + Be^{-ikx}$ und $C\cos{kx}+D\sin{kx}$ sind äquivalente Methoden, dieselbe Funktion von $x$ zu schreiben. Durch die Eulersche Formel $e^{ix}=\cos{x}+i\sin{x}$ gilt

\[\begin{align*} Ae^{ikx}+Be^{-ikx} &= A[\cos{kx}+i\sin{kx}] + B[\cos{(-kx)}+i\sin{(-kx)}] \\ &= A(\cos{kx}+i\sin{kx}) + B(\cos{kx}-i\sin{kx}) \\ &= (A+B)\cos{kx} + i(A-B)\sin{kx}. \end{align*}\]

Setzt man also $C=A+B$, $D=i(A-B)$, so gilt

\[Ae^{ikx} + Be^{-ikx} = C\cos{kx}+D\sin{kx}. \blacksquare\]

Umgekehrt ausgedrückt in $A$ und $B$ durch $C$ und $D$ ergibt sich $A=\cfrac{C-iD}{2}$, $B=\cfrac{C+iD}{2}$.

In der Quantenmechanik stellen Exponentialfunktionen bei $V=0$ laufende Wellen dar und sind bei der Behandlung freier Teilchen am bequemsten. Sinus- und Kosinusfunktionen hingegen eignen sich zur Darstellung stehender Wellen und treten beim unendlichen Potentialtopf natürlich auf.

Im Gegensatz zum unendlichen Potentialtopf gibt es diesmal keine Randbedingungen, die $k$ und $E$ beschränken. Das heißt, ein freies Teilchen kann beliebige positive Energien haben.

Separierte Lösung und Phasengeschwindigkeit

Fügt man zu $\psi(x)$ die Zeitabhängigkeit $e^{-iEt/\hbar}$ hinzu, erhält man

\[\Psi(x,t) = Ae^{ik\left(x-\frac{\hbar k}{2m}t \right)} + Be^{-ik\left(x+\frac{\hbar k}{2m}t \right)} \label{eqn:Psi_seperated_solution}\tag{4}\]

Jede beliebige Funktion von $x$ und $t$ in der speziellen Form $(x\pm vt)$ stellt eine Welle dar, die sich mit Geschwindigkeit $v$ in $\mp x$-Richtung bewegt, ohne ihre Form zu ändern. Daher stellt der erste Term in Gleichung ($\ref{eqn:Psi_seperated_solution}$) eine nach rechts laufende Welle dar, und der zweite Term stellt eine Welle mit derselben Wellenlänge und Ausbreitungsgeschwindigkeit, aber unterschiedlicher Amplitude dar, die nach links läuft. Da sie sich nur im Vorzeichen von $k$ unterscheiden, können wir schreiben

\[\Psi_k(x,t) = Ae^{i\left(kx-\frac{\hbar k^2}{2m}t \right)} \tag{5}\]

wobei die Ausbreitungsrichtung der Welle je nach Vorzeichen von $k$ wie folgt ist:

\[k \equiv \pm\frac{\sqrt{2mE}}{\hbar},\quad \begin{cases} k>0 \Rightarrow & \text{Bewegung nach rechts}, \\ k<0 \Rightarrow & \text{Bewegung nach links}. \end{cases} \tag{6}\]

Der ‘stationäre Zustand’ des freien Teilchens ist offensichtlich eine laufende Welle*, deren Wellenlänge $\lambda = 2\pi/|k|$ ist und die nach der de-Broglie-Formel

\[p = \frac{2\pi\hbar}{\lambda} = \hbar k \label{eqn:de_broglie_formula}\tag{7}\]

den Impuls hat.

*Dass ein ‘stationärer Zustand’ eine laufende Welle ist, ist physikalisch natürlich widersprüchlich. Der Grund wird bald klar.

Außerdem ist die Geschwindigkeit dieser Welle

\[v_{\text{phase}} = \left|\frac{\omega}{k}\right| = \frac{\hbar|k|}{2m} = \sqrt{\frac{E}{2m}}. \label{eqn:phase_velocity}\tag{8}\]

(Hier ist $\omega$ der Koeffizient $\cfrac{\hbar k^2}{2m}$ vor $t$.)

Diese Wellenfunktion divergiert jedoch bei Quadratintegration gegen unendlich und kann daher nicht normiert werden.

\[\int_{-\infty}^{\infty}\Psi_k^*\Psi_k dx = |A|^2\int_{-\infty}^{\infty}dx = \infty. \tag{9}\]

Das heißt, im Fall des freien Teilchens ist die separierte Lösung kein physikalisch möglicher Zustand. Freie Teilchen können nicht als stationäre Zustände existieren und können auch keinen spezifischen Energiewert haben. Intuitiv betrachtet wäre es auch seltsam, wenn sich stehende Wellen bilden würden, obwohl es an beiden Enden überhaupt keine Randbedingungen gibt.

Bestimmung der allgemeinen Lösung $\Psi(x,t)$ der zeitabhängigen Schrödinger-Gleichung

Dennoch hat diese separierte Lösung immer noch wichtige Bedeutung, denn unabhängig von der physikalischen Interpretation ist die allgemeine Lösung der zeitabhängigen Schrödinger-Gleichung eine Linearkombination der separierten Lösungen aus mathematischer Sicht. Da es jedoch in diesem Fall keine Beschränkungen gibt, hat die allgemeine Lösung die Form eines Integrals über die kontinuierliche Variable $k$ ($\int$) anstatt einer Summe über diskrete Variable $n$ ($\sum$).

\[\Psi(x,t) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{i(kx-\frac{\hbar k^2}{2m}t)}dk. \label{eqn:Psi_general_solution}\tag{10}\]

Hier spielt $\cfrac{1}{\sqrt{2\pi}}\phi(k)dk$ dieselbe Rolle wie $c_n$ in Gleichung (21) des Beitrags ‘Zeitunabhängige Schrödinger-Gleichung’.

Diese Wellenfunktion kann für geeignete $\phi(k)$ normiert werden, muss aber notwendigerweise einen Bereich von $k$ haben und daher einen Bereich von Energien und Geschwindigkeiten. Dies wird als Wellenpaket bezeichnet.

Sinusfunktionen sind räumlich unendlich ausgedehnt und können daher nicht normiert werden. Wenn man jedoch mehrere solcher Wellen überlagert, können sie durch Interferenz lokalisiert und normierbar werden.

Bestimmung von $\phi(k)$ mit dem Plancherel-Theorem

Da wir nun die Form von $\Psi(x,t)$ (Gleichung [$\ref{eqn:Psi_general_solution}$]) kennen, müssen wir nur noch $\phi(k)$ bestimmen, das die anfängliche Wellenfunktion

\[\Psi(x,0) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{ikx}dk \label{eqn:Psi_at_t_0}\tag{11}\]

erfüllt. Dies ist ein typisches Problem der Fourier-Analyse, und die Antwort kann mit dem Plancherel-Theorem gefunden werden.

\[f(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} F(k)e^{ikx}dk \Longleftrightarrow F(k)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(x)e^{-ikx}dx. \label{eqn:plancherel_theorem}\tag{12}\]

$F(k)$ wird die Fourier-Transformation von $f(x)$ genannt, und $f(x)$ ist die inverse Fourier-Transformation von $F(k)$. Wie aus Gleichung ($\ref{eqn:plancherel_theorem}$) leicht ersichtlich, unterscheiden sie sich nur im Vorzeichen des Exponenten. Natürlich gibt es die Einschränkung, dass nur Funktionen zugelassen sind, für die das Integral existiert.

Die notwendige und hinreichende Bedingung für die Existenz von $f(x)$ ist, dass $\int_{-\infty}^{\infty}|f(x)|^2dx$ endlich sein muss. In diesem Fall ist auch $\int_{-\infty}^{\infty}|F(k)|^2dk$ endlich, und

\[\int_{-\infty}^{\infty}|f(x)|^2 dx = \int_{-\infty}^{\infty}|F(k)|^2 dk\]

Manche bezeichnen die obige Gleichung als Plancherel-Theorem (so auch Wikipedia), anstatt Gleichung ($\ref{eqn:plancherel_theorem}$).

In unserem Fall garantiert die physikalische Bedingung, dass $\Psi(x,0)$ normiert sein muss, dass das Integral existiert. Daher ist die quantenmechanische Lösung für das freie Teilchen Gleichung ($\ref{eqn:Psi_general_solution}$), wobei

\[\phi(k) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\Psi(x,0)e^{-ikx}dx \label{eqn:phi}\tag{13}\]

In der Praxis kann das Integral in Gleichung ($\ref{eqn:Psi_general_solution}$) jedoch selten analytisch gelöst werden. Normalerweise werden die Werte mit numerischen Methoden am Computer berechnet.

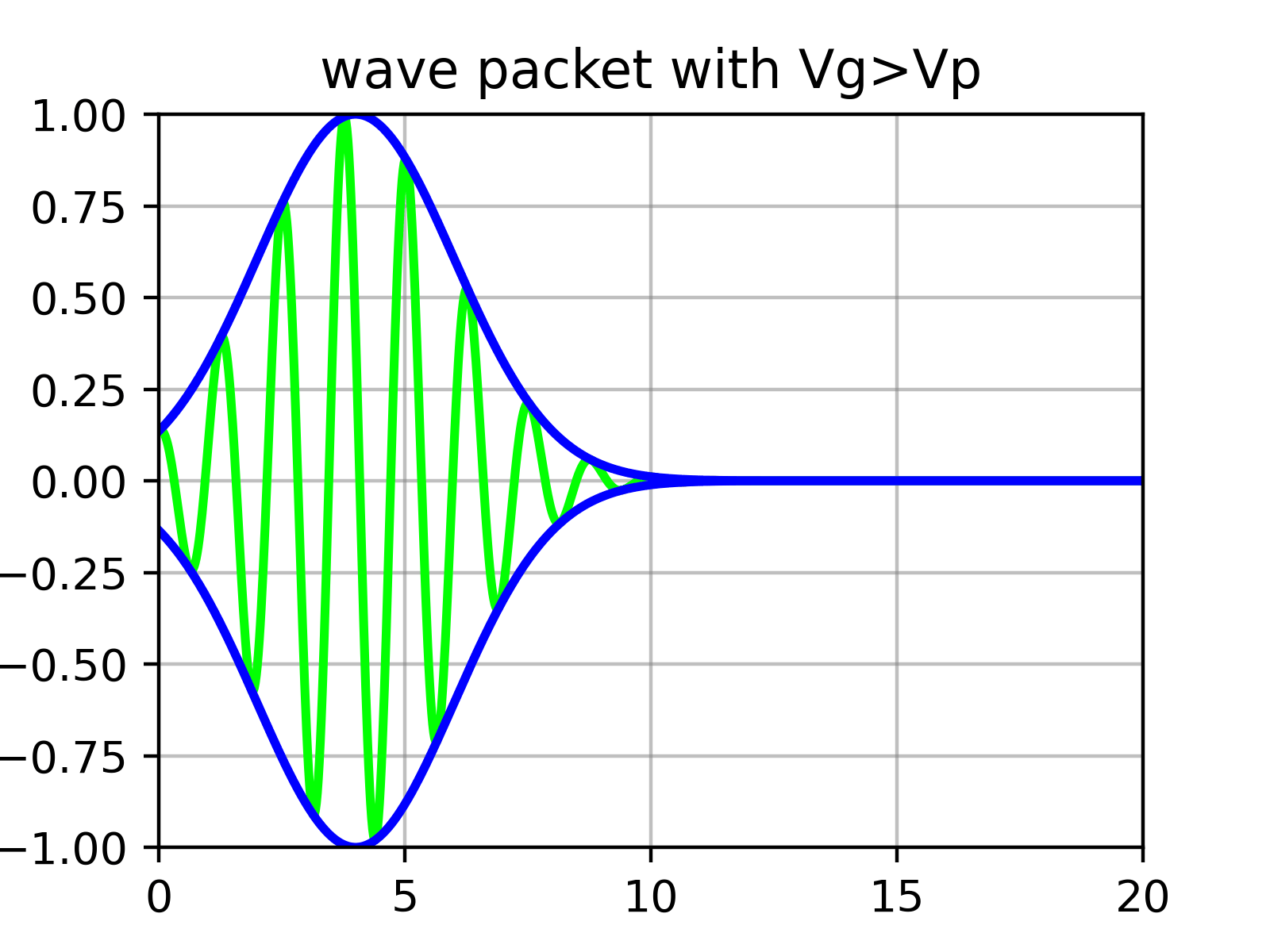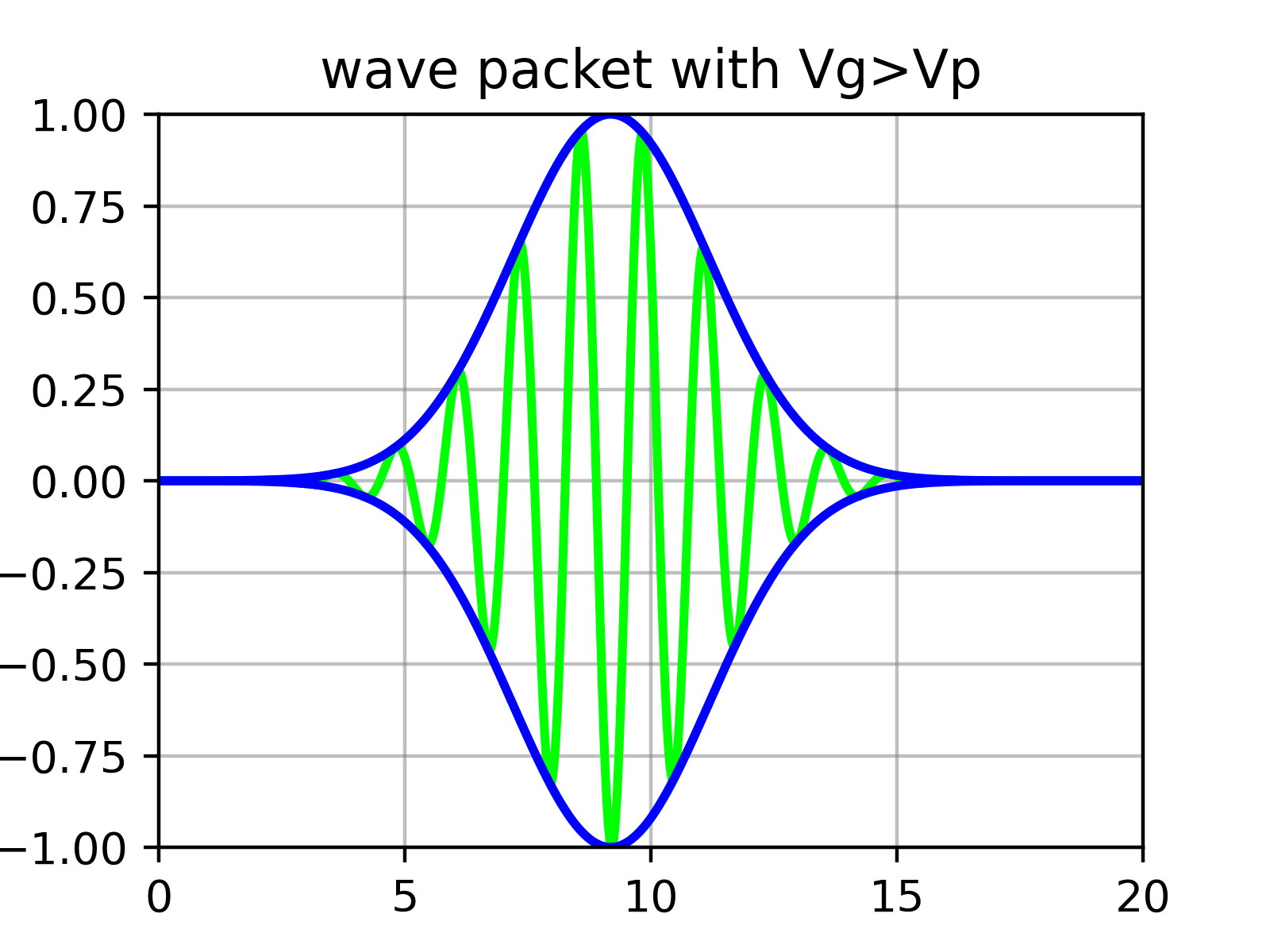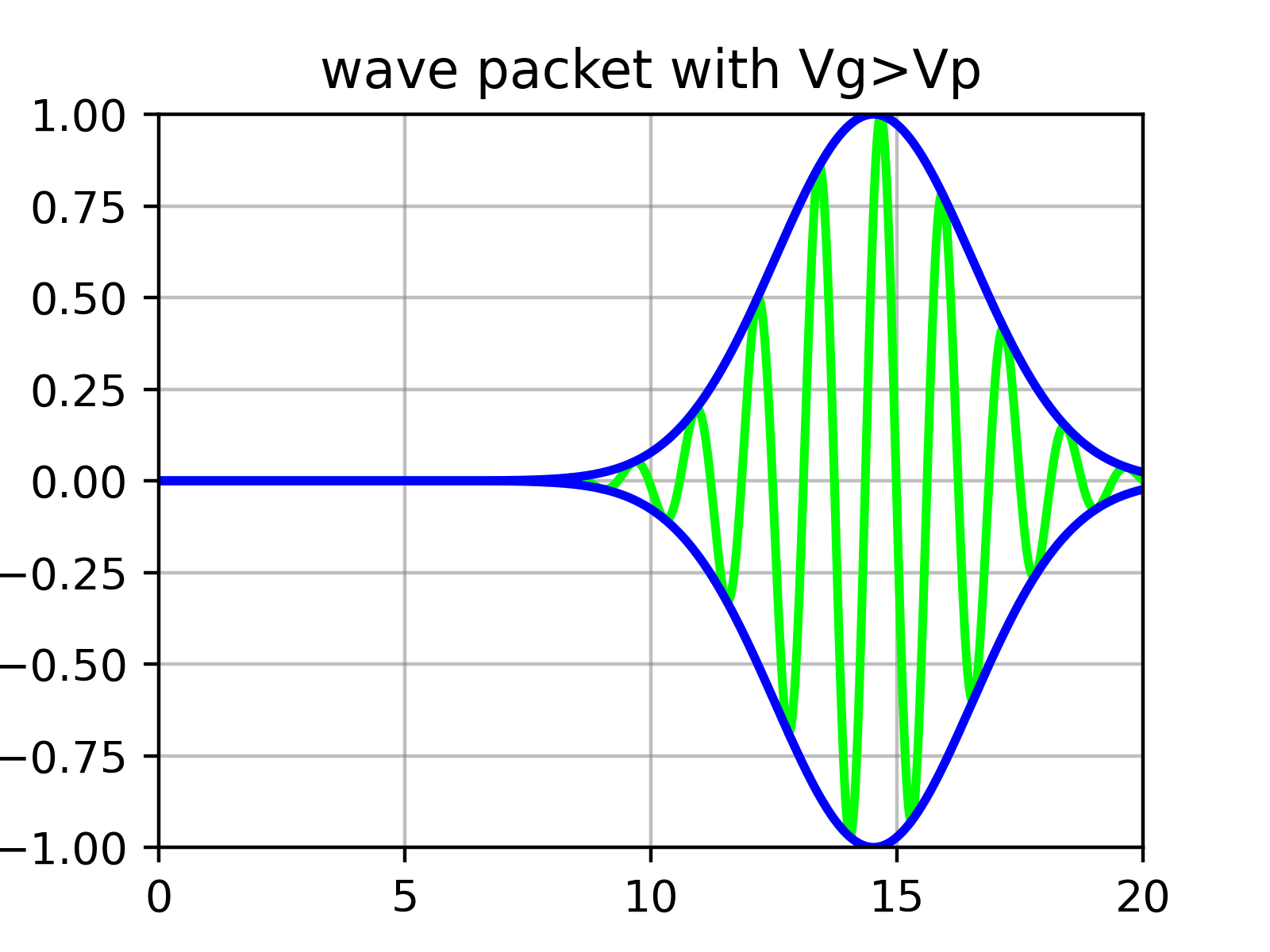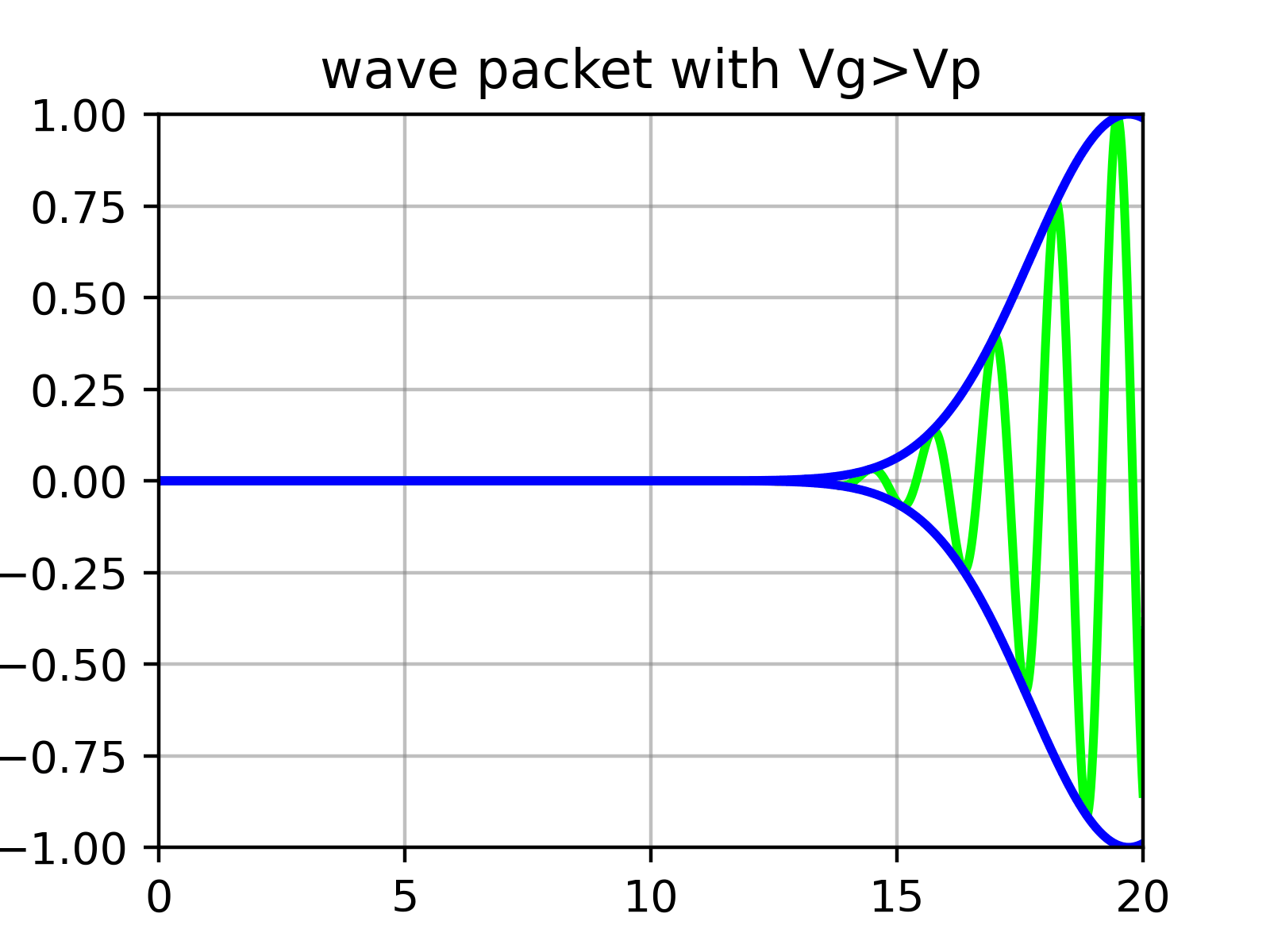
Berechnung der Gruppengeschwindigkeit des Wellenpakets und physikalische Interpretation

Im Wesentlichen ist ein Wellenpaket eine Überlagerung zahlreicher Sinusfunktionen, deren Amplituden durch $\phi$ bestimmt werden. Das heißt, das Wellenpaket hat eine ‘Einhüllende’ mit ‘Kräuselungen’ darin.

Bildlizenz und Quellenangabe

• Quellcode zur Bilderzeugung (gnuplot): yunseo-kim/physics-visualizations
• Lizenz: Mozilla Public License 2.0
• Originalautor: Ph.D. Youjun Hu
• Originallizenz: MIT License

Physikalisch entspricht die Geschwindigkeit des Teilchens nicht der Geschwindigkeit der einzelnen Kräuselungen (Phasengeschwindigkeit), die wir zuvor in Gleichung ($\ref{eqn:phase_velocity}$) berechnet haben, sondern der Geschwindigkeit der äußeren Einhüllenden (Gruppengeschwindigkeit).

Beziehung zwischen Orts- und Impulsunschärfe

Betrachten wir nur die Integrandteile $\int\phi(k)e^{ikx}dk$ aus Gleichung ($\ref{eqn:Psi_at_t_0}$) und $\int\Psi(x,0)e^{-ikx}dx$ aus Gleichung ($\ref{eqn:phi}$), um die Beziehung zwischen Orts- und Impulsunschärfe zu untersuchen.

Wenn die Ortsunschärfe klein ist

Wenn $\Psi$ im Ortsraum in einem sehr schmalen Bereich $[x_0-\delta, x_0+\delta]$ um einen Wert $x_0$ verteilt ist und außerhalb dieses Bereichs nahezu 0 ist (wenn die Ortsunschärfe klein ist), ist $e^{-ikx} \approx e^{-ikx_0}$ bezüglich $x$ nahezu konstant, sodass

\[\begin{align*} \int_{-\infty}^{\infty} \Psi(x,0)e^{-ikx}dx &\approx \int_{x_0-\delta}^{x_0+\delta} \Psi(x,0)e^{-ikx_0}dx \\ &= e^{-ikx_0}\int_{x_0-\delta}^{x_0+\delta} \Psi(x,0)dx \\ &= e^{-ipx_0/\hbar}\int_{x_0-\delta}^{x_0+\delta} \Psi(x,0)dx \quad (\because \text{Gl. }\ref{eqn:de_broglie_formula}) \end{align*}\tag{14}\]

Da der Integralterm bezüglich $p$ konstant ist, erhält $\phi$ durch den vorderen Term $e^{-ipx_0/\hbar}$ eine Sinuswellenform bezüglich $p$ im Impulsraum und ist daher über einen breiten Impulsbereich verteilt (große Impulsunschärfe).

Wenn die Impulsunschärfe klein ist

Ebenso, wenn $\phi$ im Impulsraum in einem sehr schmalen Bereich $[p_0-\delta, p_0+\delta]$ um einen Wert $p_0$ verteilt ist und außerhalb dieses Bereichs nahezu 0 ist (wenn die Impulsunschärfe klein ist), ist $e^{ikx}=e^{ipx/\hbar} \approx e^{ip_0x/\hbar}$ bezüglich $p$ nahezu konstant und $dk=\frac{1}{\hbar}dp$, sodass

\[\begin{align*} \int_{-\infty}^{\infty} \phi(k)e^{ikx}dk &= \frac{1}{\hbar}\int_{p_0-\delta}^{p_0+\delta} \phi(p)e^{ip_0x/\hbar}dp \\ &= \frac{1}{\hbar}e^{ip_0x/\hbar}\int_{p_0-\delta}^{p_0+\delta} \phi(p)dp \end{align*}\tag{15}\]

Durch den vorderen Term $e^{ip_0x/\hbar}$ erhält $\Psi$ eine Sinuswellenform bezüglich $x$ im Ortsraum und ist daher über einen breiten Ortsbereich verteilt (große Ortsunschärfe).

Schlussfolgerung

Wenn die Ortsunschärfe abnimmt, nimmt die Impulsunschärfe zu, und umgekehrt nimmt bei abnehmender Impulsunschärfe die Ortsunschärfe zu. Daher ist es quantenmechanisch unmöglich, Ort und Impuls eines freien Teilchens gleichzeitig exakt zu bestimmen.

Bildquelle

• Autor: Wikipedia-Benutzer Maschen
• Lizenz: public domain

Tatsächlich gilt dies aufgrund des Unschärfeprinzips nicht nur für freie Teilchen, sondern für alle Fälle. Das Unschärfeprinzip wird in einem separaten Beitrag behandelt.

Gruppengeschwindigkeit des Wellenpakets

Schreibt man die allgemeine Lösung aus Gleichung ($\ref{eqn:Psi_general_solution}$) mit $\omega \equiv \cfrac{\hbar k^2}{2m}$ wie in Gleichung ($\ref{eqn:phase_velocity}$) um, erhält man

\[\Psi(x,t) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \phi(k)e^{i(kx-\omega t)}dk \tag{16}\]

Die Gleichung $\omega = \cfrac{\hbar k^2}{2m}$, die $\omega$ als Funktion von $k$ darstellt, wird Dispersionsrelation genannt. Der folgende Inhalt gilt allgemein für alle Wellenpakete, unabhängig von der Dispersionsrelation.

Nehmen wir nun an, dass $\phi(k)$ eine sehr scharfe Form um einen geeigneten Wert $k_0$ herum hat. (Es ist auch in Ordnung, wenn es breit verteilt ist, aber solche Wellenpakete verformen sich sehr schnell und ändern ihre Form. Da Komponenten mit unterschiedlichen $k$ sich mit jeweils unterschiedlichen Geschwindigkeiten bewegen, verliert die gesamte ‘Gruppe’ die Bedeutung einer gut definierten Geschwindigkeit. Das heißt, die Impulsunschärfe wird groß.)
Die zu integrierende Funktion ist außer in der Nähe von $k_0$ vernachlässigbar, sodass wir die Funktion $\omega(k)$ um diesen Punkt Taylor-entwickeln können. Bis zum linearen Term erhalten wir

\[\omega(k) \approx \omega_0 + \omega_0^\prime(k-k_0)\]

Substituiert man nun $s=k-k_0$ und integriert um $k_0$:

\[\begin{align*} \Psi(x,t) &= \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\phi(k_0+s)e^{i[(k_0+s)x-(\omega_0+\omega_0^\prime s)t]}ds \\ &= \frac{1}{\sqrt{2\pi}}e^{i(k_0x-\omega_0t)}\int_{-\infty}^{\infty}\phi(k_0+s)e^{is(x-\omega_0^\prime t)}ds. \end{align*}\tag{17}\]

Der vordere Term $e^{i(k_0x-\omega_0t)}$ stellt eine Sinuswelle (‘Kräuselung’) dar, die sich mit Geschwindigkeit $\omega_0/k_0$ bewegt, und der Integralterm (‘Einhüllende’), der die Amplitude dieser Sinuswelle bestimmt, bewegt sich aufgrund des Terms $e^{is(x-\omega_0^\prime t)}$ mit Geschwindigkeit $\omega_0^\prime$. Daher ist die Phasengeschwindigkeit bei $k=k_0$

\[v_\text{phase} = \frac{\omega_0}{k_0} = \frac{\omega}{k} = \frac{\hbar k}{2m} \tag{18}\]

was den Wert aus Gleichung ($\ref{eqn:phase_velocity}$) bestätigt, und die Gruppengeschwindigkeit ist

\[v_\text{group} = \omega_0^\prime = \frac{d\omega}{dk} = \frac{\hbar k}{m} \label{eqn:group_velocity}\tag{19}\]

was das Doppelte der Phasengeschwindigkeit ist.

Vergleich mit der klassischen Mechanik

Da wir wissen, dass die klassische Mechanik auf makroskopischen Skalen gilt, sollten die durch die Quantenmechanik erhaltenen Ergebnisse bei ausreichend kleinen quantenmechanischen Unschärfen an die Berechnungsergebnisse der klassischen Mechanik angenähert werden können. Im Fall des freien Teilchens, das wir gerade behandeln, sollte bei der zuvor angenommenen sehr scharfen Form von $\phi(k)$ um einen geeigneten Wert $k_0$ herum (das heißt, wenn die Impulsunschärfe ausreichend klein ist) die quantenmechanische Gruppengeschwindigkeit $v_\text{group}$ für dasselbe $k$ und den entsprechenden Energiewert $E$ gleich der klassischen Teilchengeschwindigkeit $v_\text{classical}$ sein.

Setzt man $k\equiv \cfrac{\sqrt{2mE}}{\hbar}$ aus Gleichung ($\ref{eqn:t_independent_schrodinger_eqn}$) in die gerade berechnete Gruppengeschwindigkeit (Gleichung [$\ref{eqn:group_velocity}$]) ein, erhält man

\[v_\text{quantum} = \sqrt{\frac{2E}{m}} \tag{20}\]

und die Geschwindigkeit eines freien Teilchens mit kinetischer Energie $E$ in der klassischen Mechanik ist ebenfalls

\[v_\text{classical} = \sqrt{\frac{2E}{m}} \tag{21}\]

Da $v_\text{quantum}=v_\text{classical}$ ist, können wir bestätigen, dass das durch Anwendung der Quantenmechanik erhaltene Ergebnis eine physikalisch gültige Lösung ist.