Harmonische Additionstheoreme

TL;DR

Harmonische Additionstheoreme

• \[a\sin \theta + b\cos \theta = \sqrt{a^{2}+b^{2}} \sin(\theta+\alpha)\]

\[(\text{wobei}\ \cos \alpha = \frac{a}{\sqrt{a^{2}+b^{2}}},\ \sin \alpha = \frac{b}{\sqrt{a^{2}+b^{2}}})\]

• \[a\sin \theta + b\cos \theta = \sqrt{a^{2}+b^{2}} \cos(\theta-\beta)\]

\[(\text{wobei}\ \cos \beta = \frac{b}{\sqrt{a^{2}+b^{2}}},\ \sin \beta = \frac{a}{\sqrt{a^{2}+b^{2}}})\]

Voraussetzungen

• Additionstheoreme für trigonometrische Funktionen

Harmonische Additionstheoreme

Für eine Funktion $f(\theta) = a \cos \theta + b \sin \theta$, die als Summe trigonometrischer Funktionen dargestellt ist, existieren immer reelle Zahlen $\alpha$ und $\beta$, die $f(\theta)=\sqrt{a^2+b^2} \sin(\theta+\alpha) = \sqrt{a^2+b^2} \cos(\theta-\beta)$ erfüllen.

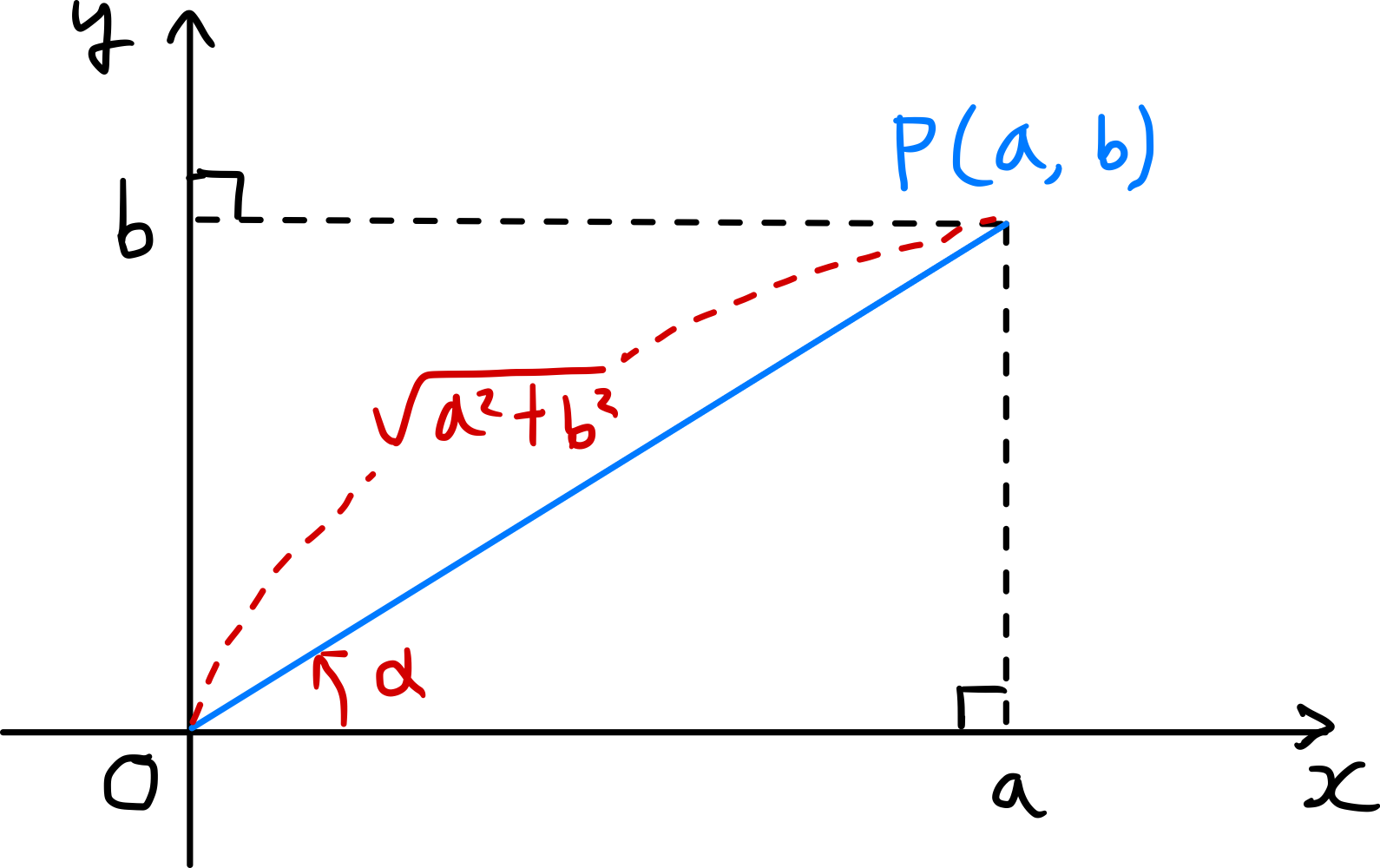
Wie in der Abbildung gezeigt, wählen wir einen Punkt $P(a,b)$ in der Koordinatenebene und bezeichnen den Winkel zwischen der Strecke $\overline{OP}$ und der positiven x-Achse als $\alpha$. Dann gilt:

\[\overline{OP} = \sqrt{a^2+b^2}\]

und

\[\cos \alpha = \frac{a}{\sqrt{a^{2} + b^{2}}},\ \sin \alpha = \frac{b}{\sqrt{a^{2} + b^{2}}} \tag{1}\]

In diesem Fall:

\[\begin{align*} a \sin \theta + b \cos \theta &= \sqrt{a^{2}+b^{2}} \left(\frac{a}{\sqrt{a^{2}+b^{2}}}\sin \theta + \frac{b}{\sqrt{a^{2}+b^{2}}}\cos \theta \right) \\ &= \sqrt{a^{2}+b^{2}}(\cos \alpha \sin \theta + \sin \alpha \cos \theta) \\ &= \sqrt{a^{2}+b^{2}} \sin(\theta + \alpha). \tag{2} \end{align*}\]

Auf ähnliche Weise können wir einen Punkt $P^{\prime}(b,a)$ wählen und den Winkel zwischen der Strecke $\overline{OP^{\prime}}$ und der positiven x-Achse als $\beta$ bezeichnen. Dann erhalten wir:

\[a \sin \theta + b \cos \theta = \sqrt{a^{2}+b^{2}}\cos(\theta-\beta). \tag{3}\] \[\text{wobei}\ \cos \beta = \frac{b}{\sqrt{a^{2}+b^{2}}},\ \sin \beta = \frac{a}{\sqrt{a^{2}+b^{2}}}.\]

Diese Umformung einer trigonometrischen Funktion der Form $a \sin \theta + b \sin \theta$ in die Form $r\sin(\theta+\alpha)$ oder $r\cos(\theta-\beta)$ wird als harmonische Addition bezeichnet.

Beispiel

Gegeben sei die Funktion $f(\theta)=-\sqrt{3}\sin \theta + \cos \left(\theta - \frac{\pi}{3} \right)$. Bestimmen Sie den Maximal- und Minimalwert der Funktion $f(\theta)$ im Intervall $[0, 2\pi]$.

1. Umformung in die Form $a\sin\theta + b\cos\theta$

Unter Verwendung der Additionstheoreme für trigonometrische Funktionen können wir die gegebene Funktion umformen:

\[\begin{align*} f(\theta) &= -\sqrt{3}\sin \theta + \cos \left(\theta - \frac{\pi}{3} \right) \\ &= -\sqrt{3}\sin \theta + \left( \cos\theta \cos\frac{\pi}{3} + \sin\theta \sin\frac{\pi}{3} \right) \\ &= -\frac{\sqrt{3}}{2}\sin\theta + \frac{1}{2}\cos\theta . \end{align*}\]

2. Umformung in die Form $r\sin(\theta+\alpha)$

Setzen wir $a=-\frac{\sqrt{3}}{2}$ und $b=\frac{1}{2}$, dann gilt:

\[r = \sqrt{a^2+b^2} = \sqrt{\frac{3}{4}+\frac{1}{4}} = 1\]

Außerdem existiert genau ein reeller Wert $\alpha$ mit $0 \leq \alpha<2\pi$, für den $\cos\alpha = a$ und $\sin\alpha = b$ gilt. Aus den Werten der trigonometrischen Funktionen für spezielle Winkel können wir schließen, dass $\alpha = \frac{5}{6}\pi$.

Somit lässt sich die gegebene Funktion $f(\theta)$ in die Form $r\sin(\theta+\alpha)$ umformen:

\[f(\theta) = \sin \left(\theta + \frac{5\pi}{6} \right).\]

3. Bestimmung des Maximal- und Minimalwerts im gegebenen Intervall

Die Funktion $f(\theta) = \sin \left(\theta + \frac{5\pi}{6} \right)$ ist eine periodische Funktion mit der Periode $2\pi$ und hat im gegebenen Intervall den Maximalwert $1$ und den Minimalwert $-1$.

\[\therefore M=1,\ m=-1\]