Energieübertragung durch Kollisionen

TL;DR

• Bei Kollisionen bleiben Gesamtenergie und Impuls erhalten
• Ionen, die alle Elektronen verloren haben, und Elektronen besitzen nur kinetische Energie
• Neutrale Atome und teilweise ionisierte Ionen haben innere Energie und können je nach Änderung der potenziellen Energie angeregt (excitation), abgeregt (deexcitation) oder ionisiert (ionization) werden
• Klassifizierung der Kollisionstypen basierend auf der Änderung der kinetischen Energie vor und nach dem Stoß:
  • Elastischer Stoß (elastic collision): Die Gesamtmenge der kinetischen Energie bleibt vor und nach dem Stoß konstant
  • Inelastischer Stoß (inelastic collision): Kinetische Energie geht während des Stoßprozesses verloren
    • Anregung (excitation)
    • Ionisation (ionization)
  • Superelastischer Stoß (superelastic collision): Kinetische Energie nimmt während des Stoßprozesses zu
    • Abregung (deexcitation)
• Energieübertragungsrate durch elastische Stöße:
  • Energieübertragungsrate bei einzelnen Stößen: $\zeta_L = \cfrac{4m_1m_2}{(m_1+m_2)^2}\cos^2\theta_2$
  • Durchschnittliche Energieübertragungsrate pro Stoß: $\overline{\zeta_L} = \cfrac{4m_1m_2}{(m_1+m_2)^2}\overline{\cos^2\theta_2} = \cfrac{2m_1m_2}{(m_1+m_2)^2}$
    • Wenn $m_1 \approx m_2$: $\overline{\zeta_L} \approx \cfrac{1}{2}$, effektive Energieübertragung führt zu schnellem thermischen Gleichgewicht
    • Wenn $m_1 \ll m_2$ oder $m_1 \gg m_2$: $\overline{\zeta_L} \approx 10^{-5}\sim 10^{-4}$, sehr geringe Energieübertragungseffizienz, schwierig thermisches Gleichgewicht zu erreichen. Dies erklärt, warum in schwach ionisierten Plasmen $T_e \gg T_i \approx T_n$ gilt, wobei Elektronentemperatur, Ionentemperatur und Temperatur neutraler Atome stark voneinander abweichen.
• Energieübertragungsrate durch inelastische Stöße:
  • Maximale innere Energieumwandlungsrate bei einzelnen Stößen: $\zeta_L = \cfrac{\Delta U_\text{max}}{\cfrac{1}{2}m_1v_1^2} = \cfrac{m_2}{m_1+m_2}\cos^2\theta_2$
  • Durchschnittliche maximale innere Energieumwandlungsrate: $\overline{\zeta_L} = \cfrac{m_2}{m_1+m_2}\overline{\cos^2\theta_2} = \cfrac{m_2}{2(m_1+m_2)}$
    • Wenn $m_1 \approx m_2$: $\overline{\zeta_L} \approx \cfrac{1}{4}$
    • Wenn $m_1 \gg m_2$: $\overline{\zeta_L} \approx 10^{-5}\sim 10^{-4}$
    • Wenn $m_1 \ll m_2$: $\overline{\zeta_L} = \cfrac{1}{2}$, am effizientesten zur Erhöhung der inneren Energie des Kollisionsobjekts (Ion oder neutrales Atom) und Erzeugung angeregter Zustände. Dies erklärt, warum Elektronenionisation (Plasmaerzeugung), Anregung (Emission) und Moleküldissoziation (Radikalerzeugung) leicht auftreten.

Prerequisites

• Subatomare Teilchen und Bestandteile des Atoms

Teilchenkollisionen in Plasmen

• Bei Kollisionen bleiben Gesamtenergie und Impuls erhalten
• Ionen, die alle Elektronen verloren haben, und Elektronen besitzen nur kinetische Energie
• Neutrale Atome und teilweise ionisierte Ionen haben innere Energie und können je nach Änderung der potenziellen Energie angeregt (excitation), abgeregt (deexcitation) oder ionisiert (ionization) werden
• Klassifizierung der Kollisionstypen basierend auf der Änderung der kinetischen Energie vor und nach dem Stoß:
  • Elastischer Stoß (elastic collision): Die Gesamtmenge der kinetischen Energie bleibt vor und nach dem Stoß konstant
  • Inelastischer Stoß (inelastic collision): Kinetische Energie geht während des Stoßprozesses verloren
    • Anregung (excitation)
    • Ionisation (ionization)
  • Superelastischer Stoß (superelastic collision): Kinetische Energie nimmt während des Stoßprozesses zu
    • Abregung (deexcitation)

Energieübertragung durch elastische Stöße

Energieübertragungsrate bei einzelnen Stößen

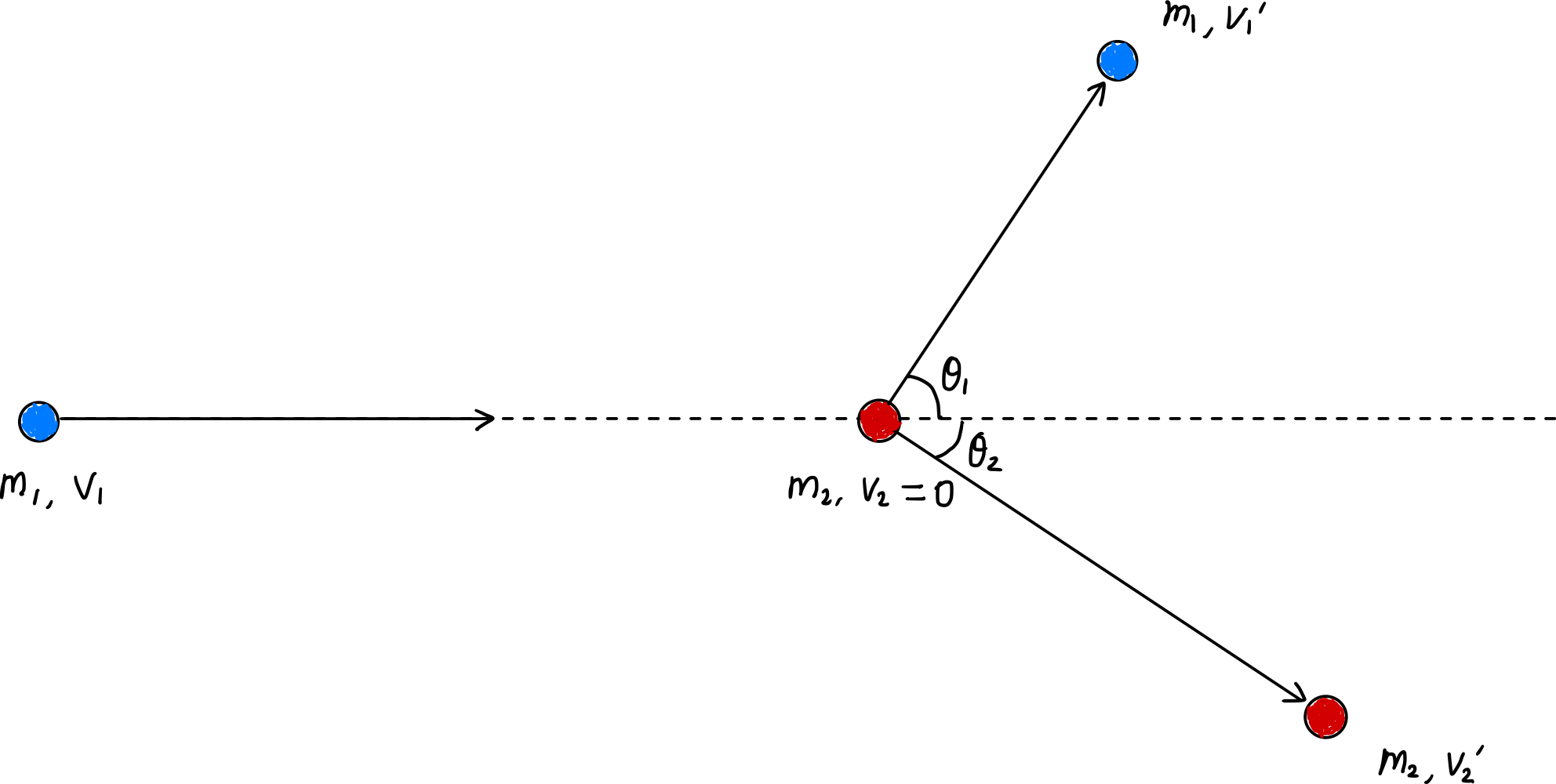
Bei elastischen Stößen bleiben Impuls und kinetische Energie vor und nach dem Stoß erhalten.

Die Impulserhaltungsgleichungen für die x- und y-Achse lauten:

\[\begin{gather*} m_1v_1 = m_1v_1^{\prime}\cos\theta_1 + m_2v_2^{\prime}\cos\theta_2, \label{eqn:momentum_conservation_x}\tag{1} \\ m_1v_1^{\prime}\sin\theta_1 = m_2v_2^{\prime}\sin\theta_2 \label{eqn:momentum_conservation_y}\tag{2} \end{gather*}\]

Aufgrund der Energieerhaltung gilt:

\[\frac{1}{2}m_1v_1^2 = \frac{1}{2}m_1{v_1^{\prime}}^2 + \frac{1}{2}m_2{v_2^{\prime}}^2\] \[v_1^2 = {v_1^{\prime}}^2 + \frac{m_2}{m_1}{v_2^{\prime}}^2 \label{eqn:energy_conservation}\tag{3}\]

Aus Gleichung ($\ref{eqn:momentum_conservation_x}$) folgt:

\[m_1 v_1^{\prime} \cos \theta_1 = m_1v_1 - m_2v_2^{\prime} \cos \theta_2 \label{eqn:momentum_conservation_x_2}\tag{4}\]

Quadrieren und Addieren der Gleichungen ($\ref{eqn:momentum_conservation_y}$) und ($\ref{eqn:momentum_conservation_x_2}$) ergibt:

\[\begin{align*} (m_1v_1^{\prime})^2 &= (m_2 v_2^\prime \sin \theta_2)^2 + (m_1 v_1 - m_2 v_2^\prime \cos \theta_2)^2 \\ &= m_1^2 v_1^2 - 2 m_1 m_2 v_1 v_2^\prime \cos \theta_2 + m_2^2 {v_2^\prime}^2 \tag{5} \end{align*}\]

Division beider Seiten durch $m_1^2$ ergibt:

\[{v_1^{\prime}}^2 = v_1^2 - 2 \frac{m_2}{m_1} v_1 v_2^\prime \cos \theta_2 + \left(\frac{m_2}{m_1}\right)^2 {v_2^\prime}^2 \label{eqn:momentum_conservation}\tag{6}\]

Einsetzen von Gleichung ($\ref{eqn:energy_conservation}$) führt zu:

\[\begin{gather*} \left( \frac{m_2}{m_1} \right) {v_2^\prime}^2 = 2 \left( \frac{m_2}{m_1} \right) v_1 v_2^\prime \cos \theta_2 - \left( \frac{m_2}{m_1} \right)^2 {v_2^\prime}^2 \\ 2v_1 \cos \theta_2 = \left(\frac{m_1 + m_2}{m_1} \right) v_2^\prime \\ v_2^{\prime} = \frac{2m_1v_1\cos\theta_2}{m_1 + m_2}. \label{eqn:v_2_prime}\tag{7} \end{gather*}\]

Daraus ergibt sich die Energieübertragungsrate $\zeta_L$:

\[\begin{align*} \therefore \zeta_L &= \frac{\cfrac{1}{2}m_2{v_2^\prime}^2}{\cfrac{1}{2}m_1v_1^2} = \frac{m_2}{m_1v_1^2} {\left(\frac{2m_1v_1\cos\theta_2}{m_1 + m_2} \right)}^2 \\ &= \frac{4m_1m_2}{(m_1+m_2)^2}\cos^2\theta_2. \quad \blacksquare \label{eqn:elastic_E_transfer_rate}\tag{8} \end{align*}\]

Durchschnittliche Energieübertragungsrate pro Stoß

Für Winkel von 0 bis 2π gilt $\sin^2{\theta_2}+\cos^2{\theta_2}=1$ und $\overline{\sin^2{\theta_2}}=\overline{\cos^2{\theta_2}}$, daher:

\[\begin{align*} \overline{\cos^2{\theta_2}} &= \overline{(1-\sin^2{\theta_2})} = 1 - \overline{\sin^2{\theta_2}} \\ &= 1 - \overline{\cos^2{\theta_2}} \end{align*}\] \[\begin{gather*} 2 \cdot \overline{\cos^2{\theta_2}} = 1 \\ \overline{\cos^2{\theta_2}} = \frac{1}{2}. \end{gather*}\]

Einsetzen in Gleichung ($\ref{eqn:elastic_E_transfer_rate}$) ergibt:

\[\overline{\zeta_L} = \frac{4m_1m_2}{(m_1+m_2)^2}\overline{\cos^2\theta_2} = \frac{2m_1m_2}{(m_1+m_2)^2}. \quad \blacksquare \label{eqn:elastic_E_mean_transfer_rate}\tag{9}\]

Wenn $m_1 \approx m_2$

Dies gilt für Elektron-Elektron-, Ion-Ion-, Neutralatom-Neutralatom- und Ion-Neutralatom-Stöße. In diesem Fall:

\[\overline{\zeta_L} = \frac{2m_1m_2}{(m_1+m_2)^2} \approx \frac{1}{2} \label{eqn:elastic_similar_m}\tag{10}\]

Es findet eine effektive Energieübertragung statt, die schnell zum thermischen Gleichgewicht führt.

Wenn $m_1 \ll m_2$ oder $m_1 \gg m_2$

Dies gilt für Elektron-Ion-, Elektron-Neutralatom-, Ion-Elektron- und Neutralatom-Elektron-Stöße. In diesem Fall:

\[\overline{\zeta_L} = \frac{2m_1m_2}{(m_1+m_2)^2} \approx \frac{2m_1}{m_2}\text{ (für }m_1 \ll m_2 \text{)} \approx 10^{-5}\sim 10^{-4} \label{eqn:elastic_different_m}\tag{11}\]

Die Energieübertragungseffizienz ist sehr gering, was es schwierig macht, das thermische Gleichgewicht zu erreichen. Dies erklärt, warum in schwach ionisierten Plasmen $T_e \gg T_i \approx T_n$ gilt, wobei die Elektronentemperatur, Ionentemperatur und Temperatur der neutralen Atome stark voneinander abweichen.

Energieübertragung durch inelastische Stöße

Maximale innere Energieumwandlungsrate bei einzelnen Stößen

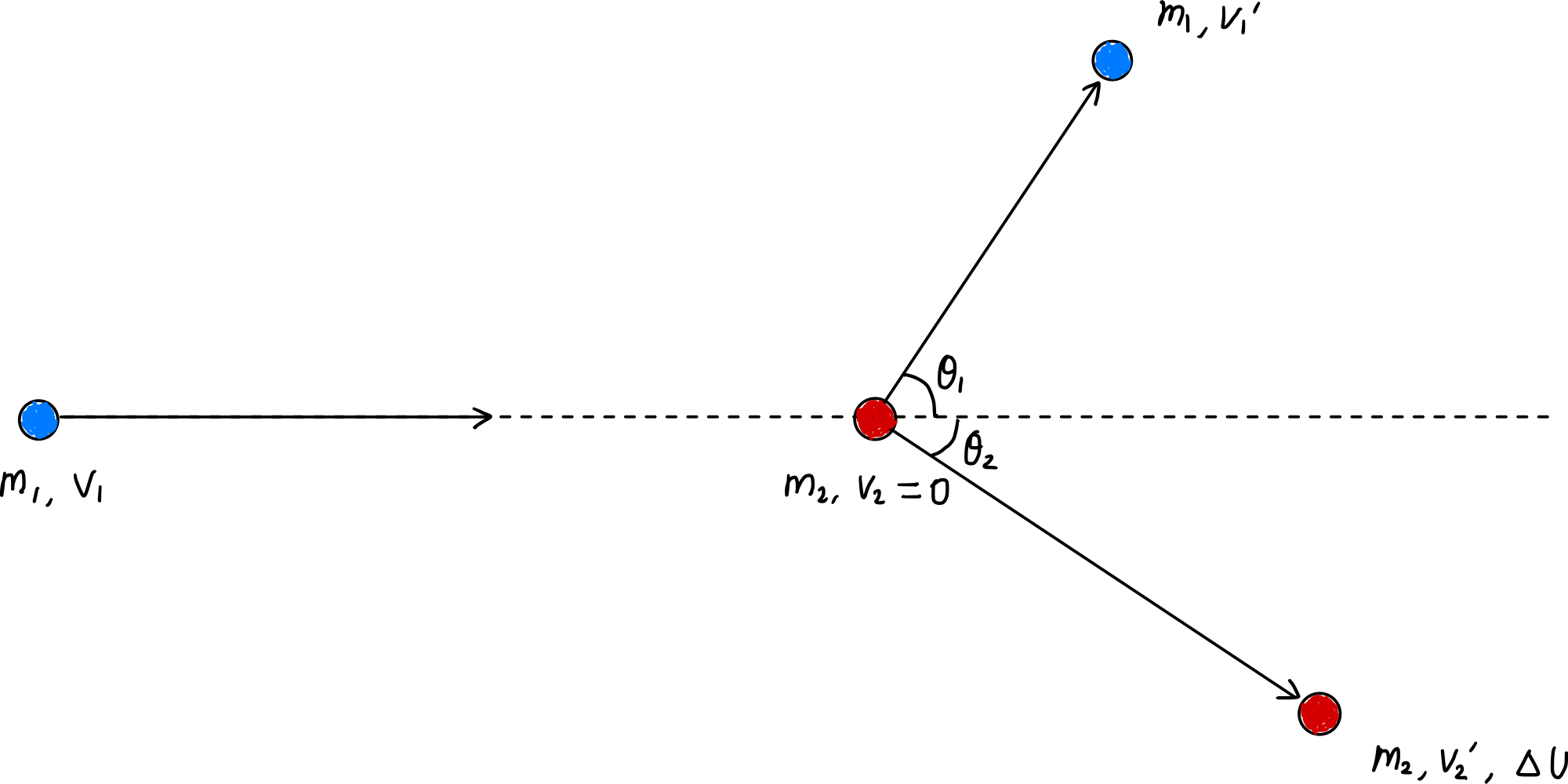
Die Impulserhaltung (Gleichung [$\ref{eqn:momentum_conservation}$]) gilt auch in diesem Fall, aber die kinetische Energie wird bei inelastischen Stößen nicht erhalten. Die durch den inelastischen Stoß verlorene kinetische Energie wird in innere Energie $\Delta U$ umgewandelt:

\[\Delta U = \frac{1}{2} m_1 v_1^2 - \left( \frac{1}{2} m_1 {v_1^{\prime}}^2 + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right) \label{eqn:delta_U}\tag{12}\]

Einsetzen von Gleichung ($\ref{eqn:momentum_conservation}$) und Umformen ergibt:

\(\begin{align*} \Delta U &= \frac{1}{2} m_1 v_1^2 - \left[ \frac{1}{2} m_1 \left( v_1^2 - 2 \frac{m_2}{m_1} v_1 v_2^{\prime} \cos \theta_2 + \left( \frac{m_2}{m_1} v_2^{\prime} \right)^2 \right) + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right] \\ &= \frac{1}{2} m_1 v_1^2 - \left[ \frac{1}{2} m_1 v_1^2 - m_2 v_1 v_2^{\prime} \cos \theta_2 + \frac{1}{2} \frac{m_2^2}{m_1} {v_2^{\prime}}^2 + \frac{1}{2} m_2 {v_2^{\prime}}^2 \right] \\ &= m_2 v_1 v_2^{\prime} \cos \theta_2 - \frac{1}{2}m_2{v_2^{\prime}}^2\left(\frac{m_1 + m_2}{m_1}\right) \label{eqn:delta_U_2}\tag{13} \end{align*}\).

Differenzieren von $\Delta U$ nach $v_2^\prime$ und Nullsetzen der Ableitung ergibt den Extrempunkt und den Maximalwert:

\[\cfrac{d \Delta U}{d v_2^{\prime}} = m_2 v_1 \cos \theta_2 - m_2 v_2^{\prime} \left( \frac{m_1 + m_2}{m_1} \right) = 0 \tag{14}\] \[\begin{gather*} v_2^{\prime} \left( \frac{m_1 + m_2}{m_1} \right) = v_1 \cos \theta_2 \\ v_2^\prime = \frac{m_1v_1\cos\theta_2}{m_1+m_2}. \end{gather*}\] \[\therefore v_2^{\prime} = \frac{m_1v_1\cos\theta_2}{m_1+m_2} \text{ bei } \Delta U_\text{max} = \frac{1}{2}\frac{m_1m_2 v_1^2 \cos^2\theta_2}{m_1 + m_2}. \label{eqn:delta_U_max}\tag{15}\]

Daraus ergibt sich die maximale Umwandlungsrate $\zeta_L$ von kinetischer Energie in innere Energie bei einem einzelnen inelastischen Stoß:

\[\zeta_L = \frac{\Delta U_\text{max}}{\cfrac{1}{2}m_1v_1^2} = \frac{m_2}{m_1+m_2}\cos^2\theta_2. \quad \blacksquare \label{eqn:inelastic_E_transfer_rate}\tag{16}\]

Durchschnittliche maximale innere Energieumwandlungsrate

Analog dazu ergibt sich durch Einsetzen von $\overline{\cos^2{\theta_2}} = \cfrac{1}{2}$ in Gleichung ($\ref{eqn:inelastic_E_transfer_rate}$):

\[\overline{\zeta_L} = \frac{m_2}{m_1+m_2}\overline{\cos^2\theta_2} = \frac{m_2}{2(m_1+m_2)}. \label{eqn:inelastic_E_mean_transfer_rate}\tag{17}\]

Wenn $m_1 \approx m_2$

Dies gilt für Ion-Ion-, Ion-Neutralatom- und Neutralatom-Neutralatom-Stöße.

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} = \frac{1}{4}. \label{eqn:inelastic_similar_m}\tag{18}\]

Wenn $m_1 \gg m_2$

Dies gilt für Ion-Elektron- und Neutralatom-Elektron-Stöße.

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} \approx \frac{m_2}{2m_1} \approx 10^{-5}\sim 10^{-4}. \label{eqn:inelastic_ion_electron}\tag{19}\]

Wenn $m_1 \ll m_2$

Dies gilt für Elektron-Ion- und Elektron-Neutralatom-Stöße. Während die ersten beiden Fälle nicht wesentlich von elastischen Stößen abweichen, zeigt dieser dritte Fall einen wichtigen Unterschied. In diesem Fall:

\[\overline{\zeta_L} = \frac{m_2}{2(m_1+m_2)} \approx \frac{m_2}{2m_2} = \frac{1}{2} \label{eqn:inelastic_electron_ion}\tag{20}\]

Dies ist am effizientesten, um die innere Energie des Stoßobjekts (Ion oder neutrales Atom) zu erhöhen und angeregte Zustände zu erzeugen. Dies erklärt, warum Elektronenionisation (Plasmaerzeugung), Anregung (Emission) und Moleküldissoziation (Radikalerzeugung) leicht auftreten, was in späteren Diskussionen behandelt wird.