Definition und Temperaturkonzept des Plasmas sowie die Saha-Gleichung

TL;DR

• Plasma: Ein quasineutrales Gas aus geladenen und neutralen Teilchen, das kollektives Verhalten zeigt
• ‘Kollektives Verhalten’ des Plasmas:
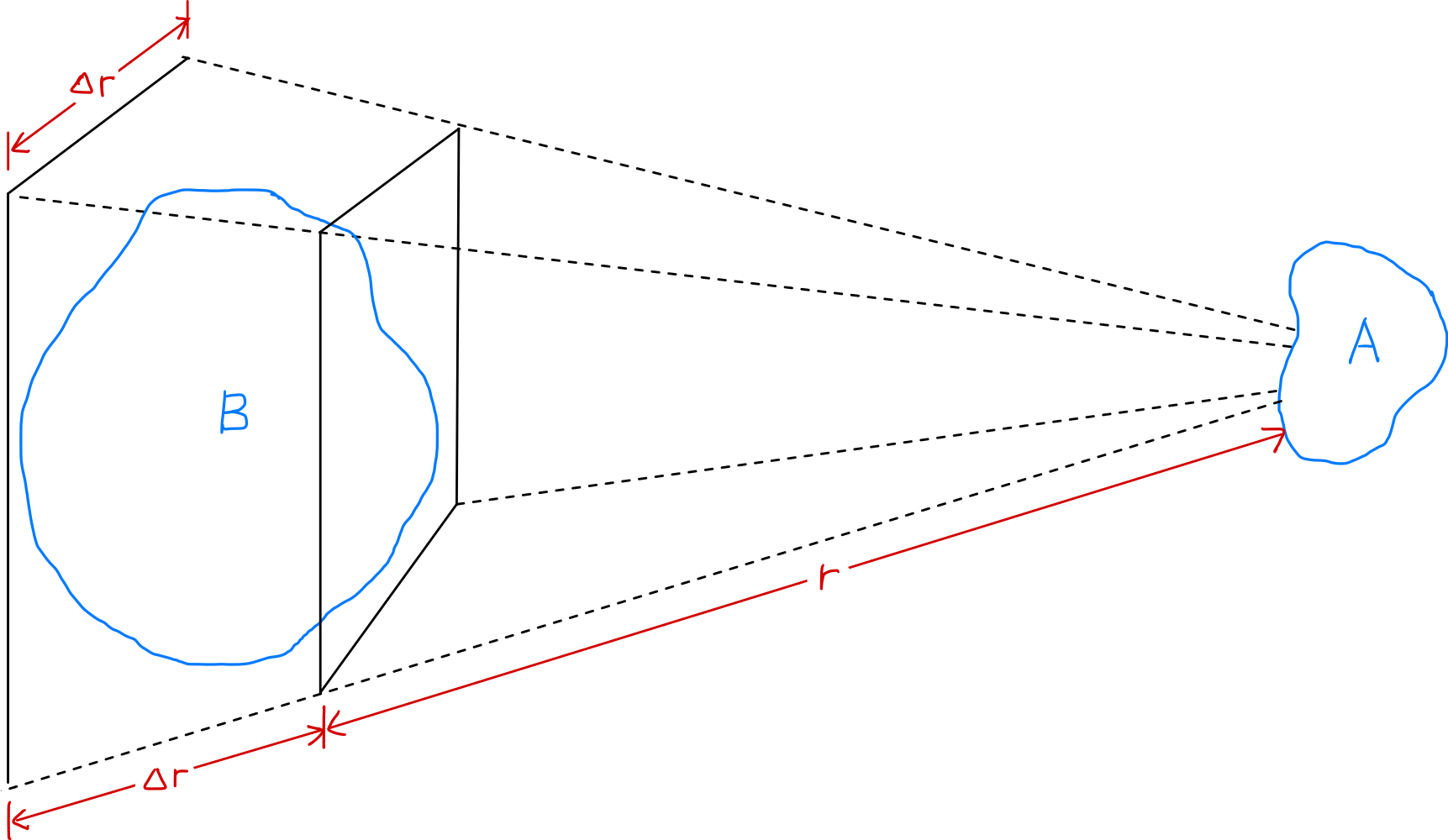
  • Die elektrische Kraft zwischen zwei Bereichen A und B im Plasma nimmt mit zunehmender Entfernung mit 1/r² ab
  • Bei konstantem Raumwinkel (Δr/r) nimmt jedoch das Volumen des Plasmabereichs B, der A beeinflussen kann, mit r³ zu
  • Daher können Teile des Plasmas auch über große Entfernungen signifikante Kräfte aufeinander ausüben
• Saha-Gleichung: Beziehung zwischen Ionisationszustand, Temperatur und Druck eines Gases im thermischen Gleichgewicht

\[\frac{n_{i+1}n_e}{n_i} = \frac{2}{\lambda_{\text{th}}^3}\frac{g_{i+1}}{g_i}\exp{\left[-\frac{\epsilon_{i+1}-\epsilon_i}{k_B T}\right]}\]

• Temperaturkonzept in der Plasmaphysik:
  • In Gasen und Plasmen ist die mittlere kinetische Energie pro Teilchen eng mit der Temperatur verbunden, und diese beiden sind austauschbare physikalische Größen
  • In der Plasmaphysik ist es üblich, die Temperatur in der Energieeinheit eV als Wert von kT auszudrücken
    • 1 eV = 11600 K
  • Plasmen können gleichzeitig mehrere verschiedene Temperaturen haben, insbesondere können die Elektronentemperatur (Te) und die Ionentemperatur (Ti) in manchen Fällen stark voneinander abweichen
• Kaltes Plasma vs. heißes Plasma:
  • Plasmatemperatur:
    • Kaltes Plasma: Te (>10.000°C) ≫ Ti ≈ Tg (∼100°C) → Nichtgleichgewichtsplasma
    • Heißes (thermisches) Plasma: Te ≈ Ti ≈ Tg (>10.000°C) → Gleichgewichtsplasma
  • Plasmadichte:
    • Kaltes Plasma: ng ≫ ni ≈ ne → Geringer Ionisationsgrad, hauptsächlich neutrale Teilchen
    • Heißes (thermisches) Plasma: ng ≈ ni ≈ ne → Hoher Ionisationsgrad
  • Wärmekapazität des Plasmas:
    • Kaltes Plasma: Hohe Elektronentemperatur, aber geringe Dichte; hauptsächlich relativ kalte neutrale Teilchen, daher geringe Wärmekapazität und nicht heiß
    • Heißes (thermisches) Plasma: Hohe Temperatur von Elektronen, Ionen und neutralen Teilchen, daher hohe Wärmekapazität und heiß

Voraussetzungen

• Subatomare Teilchen und Bestandteile des Atoms
• Maxwell-Boltzmann-Verteilung (Statistische Mechanik)
• Masse und Energie, Teilchen und Wellen
• Symmetrie und Erhaltungssätze (Quantenmechanik), Entartung (degeneracy)

Definition des Plasmas

In Texten, die Plasma für Nicht-Fachleute erklären, wird Plasma oft wie folgt definiert:

Der vierte Aggregatzustand der Materie, der nach Festkörper, Flüssigkeit und Gas kommt, und der durch Erhitzen eines Gases bis zur Ionisation seiner Atome in Elektronen und positive Ionen in einem Ultrahochtemperaturzustand erreicht wird

Dies ist nicht falsch, und auch die Website des Korea Institute of Fusion Energy stellt es so vor. Es ist auch die populäre Definition, die man leicht findet, wenn man nach Plasma sucht.

Allerdings ist dieser Ausdruck zwar korrekt, kann aber nicht als strenge Definition betrachtet werden. Auch Gase in unserer Umgebung bei Raumtemperatur und Normaldruck sind zu einem extrem geringen Anteil ionisiert, aber wir bezeichnen sie nicht als Plasma. Wenn man eine Ionenverbindung wie Natriumchlorid in Wasser auflöst, trennt sie sich in geladene Ionen, aber auch diese Lösung ist kein Plasma.
Mit anderen Worten, Plasma ist zwar ein ionisierter Zustand der Materie, aber nicht alles, was ionisiert ist, ist ein Plasma.

Genauer kann Plasma wie folgt definiert werden:

Ein Plasma ist ein quasineutrales Gas aus geladenen und neutralen Teilchen, das kollektives Verhalten zeigt.
A plasma is a quasineutral gas of charged and neutral particles which exhibits collective behavior.

von Francis F. Chen

Was “Quasineutralität” bedeutet, werden wir später bei der Behandlung der Debye-Abschirmung erfahren. Hier wollen wir untersuchen, was das “kollektive Verhalten” des Plasmas bedeutet.

Kollektives Verhalten des Plasmas

Bei einem nicht-ionisierten Gas aus neutralen Teilchen ist die resultierende elektromagnetische Kraft auf jedes Gasmolekül Null, da es elektrisch neutral ist, und auch der Einfluss der Schwerkraft kann vernachlässigt werden. Die Moleküle bewegen sich ungestört, bis sie mit anderen Molekülen kollidieren, und diese Kollisionen bestimmen die Bewegung der Teilchen. Selbst wenn einige Teilchen ionisiert sind und eine Ladung tragen, ist der Anteil der ionisierten Teilchen am gesamten Gas so gering, dass der elektrische Einfluss dieser geladenen Teilchen mit 1/r² mit der Entfernung abnimmt und nicht weit reicht.

In einem Plasma, das viele geladene Teilchen enthält, ist die Situation jedoch völlig anders. Die Bewegung der geladenen Teilchen kann zu lokalen Konzentrationen von positiven oder negativen Ladungen führen, was elektrische Felder erzeugt. Außerdem erzeugt die Bewegung von Ladungen Ströme, und Ströme erzeugen Magnetfelder. Diese elektrischen und magnetischen Felder können andere Teilchen auch in großer Entfernung beeinflussen, ohne dass direkte Kollisionen stattfinden.

Betrachten wir, wie sich die Stärke der elektrischen Kraft zwischen zwei leicht geladenen Plasmabereichen A und B mit der Entfernung r ändert. Die Coulomb-Kraft zwischen A und B nimmt mit zunehmender Entfernung mit 1/r² ab. Bei konstantem Raumwinkel (Δr/r) nimmt jedoch das Volumen des Plasmabereichs B, der A beeinflussen kann, mit r³ zu. Daher können Teile des Plasmas auch über große Entfernungen signifikante Kräfte aufeinander ausüben. Diese weitreichenden elektrischen Kräfte ermöglichen es dem Plasma, eine Vielzahl von Bewegungsmustern zu zeigen, und sind auch der Grund, warum die Plasmaphysik als eigenständiges Fachgebiet existiert. “Kollektives Verhalten” bedeutet, dass die Bewegung eines Bereichs nicht nur von den lokalen Bedingungen in diesem Bereich abhängt, sondern auch vom Zustand des Plasmas in weit entfernten Bereichen beeinflusst wird.

Saha-Gleichung

Die Saha-Gleichung ist eine Beziehung zwischen dem Ionisationszustand, der Temperatur und dem Druck eines Gases im thermischen Gleichgewicht, die vom indischen Astrophysiker Meghnad Saha entwickelt wurde.

\[\frac{n_{i+1}n_e}{n_i} = \frac{2}{\lambda_{\text{th}}^3}\frac{g_{i+1}}{g_i}\exp{\left[-\frac{\epsilon_{i+1}-\epsilon_i}{k_B T}\right]} \label{eqn:saha_eqn}\tag{1}\]

• $n_i$: Dichte der i-fach positiv geladenen Ionen (Ionen, die i Elektronen verloren haben)
• $g_i$: Entartung des Zustands der i-fach positiv geladenen Ionen
• $\epsilon_i$: Energie, die benötigt wird, um i Elektronen von einem neutralen Atom zu entfernen und ein i-fach positiv geladenes Ion zu erzeugen
  • $\epsilon_{i+1}-\epsilon_i$: (i+1)-te Ionisierungsenergie
• $n_e$: Elektronendichte
• $k_B$: Boltzmann-Konstante
• $\lambda_{\text{th}}$: Thermische de Broglie-Wellenlänge (durchschnittliche de Broglie-Wellenlänge der Elektronen im Gas bei gegebener Temperatur)

\[\lambda_{\text{th}} \equiv \frac{h}{\sqrt{2\pi m_e k_B T}} \quad \text{ (}h\text{: Planck-Konstante)} \label{eqn:lambda_th}\tag{2}\]

• $m_e$: Elektronenmasse
• $T$: Temperatur des Gases

Wenn nur eine Stufe der Ionisation wichtig ist und die Erzeugung von zweifach oder höher geladenen Ionen vernachlässigt werden kann, kann man $n_1=n_i=n_e$, $n_0=n_n$, $U_i = \epsilon = \epsilon_1$, $i=0$ setzen und die Gleichung wie folgt vereinfachen:

\[\begin{align*} \frac{n_i^2}{n_n} &= \frac{2}{\lambda_{th}^3}\frac{g_1}{g_0}\exp{\left[-\frac{\epsilon}{k_B T} \right]} \label{eqn:saha_eqn_approx}\tag{3}\\ &= 2\left(\frac{2\pi m_e k_B T}{h^2}\right)^{3/2}\frac{g_1}{g_0}e^{-U_i/{k_B T}} \\ &= 2\frac{g_1}{g_0}\left(\frac{2\pi m_e k_B}{h^2}\right)^{3/2}T^{3/2}e^{-U_i/{k_B T}}. \label{eqn:saha_eqn_approx_2}\tag{4} \end{align*}\]

Ionisationsgrad der Luft (Stickstoff) bei Raumtemperatur und Normaldruck

In der obigen Gleichung variiert der Wert von $2 \cfrac{g_1}{g_0}$ je nach Gaskomponente, aber in vielen Fällen liegt die Größenordnung dieses Wertes bei 1. Daher können wir näherungsweise wie folgt schreiben:

\[\frac{n_i^2}{n_n} \approx \left(\frac{2\pi m_e k_B}{h^2}\right)^{3/2} T^{3/2} e^{-U_i/{k_B T}}.\]

Im SI-Einheitensystem sind die Werte der Grundkonstanten $m_e$, $k_B$, $h$ jeweils:

• $m_e \approx 9,11 \times 10^{-31} \mathrm{kg}$
• $k_B \approx 1,38 \times 10^{-23} \mathrm{J/K}$
• $h \approx 6,63 \times 10^{-34} \mathrm{J \cdot s}$

Wenn wir diese in die obige Gleichung einsetzen, erhalten wir:

\[\frac{n_i^2}{n_n} \approx 2,4 \times 10^{21}\ T^{3/2} e^{-U_i/{k_B T}}. \label{eqn:fractional_ionization}\tag{5}\]

Daraus können wir den Näherungswert für den Ionisationsgrad $n_i/(n_n + n_i) \approx n_i/n_n$ von Stickstoff ($U_i \approx 14,5\mathrm{eV} \approx 2,32 \times 10^{-18}\mathrm{J}$) bei Raumtemperatur und Normaldruck ($n_n \approx 3 \times 10^{25} \mathrm{m^{-3}}$, $T\approx 300\mathrm{K}$) berechnen:

\[\frac{n_i}{n_n} \approx 10^{-122}\]

Dies zeigt einen extrem niedrigen Anteil. Das ist der Grund, warum wir im Gegensatz zur Weltraumumgebung in der Atmosphäre nahe der Erdoberfläche und des Meeresspiegels natürlich kaum Plasma antreffen können.

Das Konzept der Temperatur in der Plasmaphysik

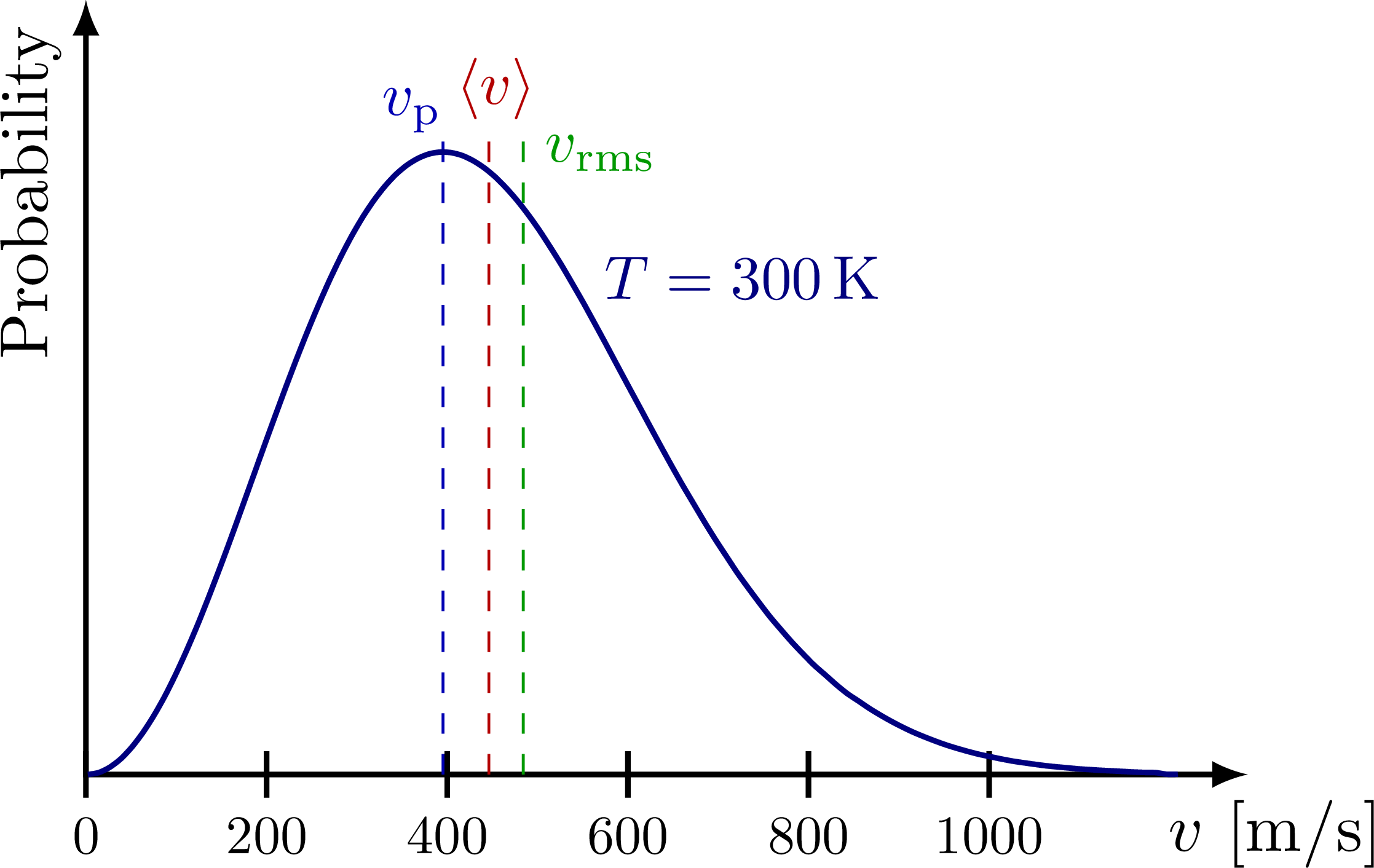
Die Geschwindigkeiten der Teilchen in einem Gas im thermischen Gleichgewicht folgen im Allgemeinen der Maxwell-Boltzmann-Verteilung:

\[f(v) = \left(\frac{m}{2\pi k_B T} \right)^{3/2} 4\pi v^2 \exp{\left(-\frac{mv^2}{2k_B T} \right)} \label{eqn:maxwell_boltzmann_dist}\tag{6}\]

Bildquelle

• Autor: TikZ.net author Izaak Neutelings
• Lizenz: CC BY-SA 4.0

• Wahrscheinlichste Geschwindigkeit (most probable speed): $v_p = \sqrt{\cfrac{2k_B T}{m}}$
• Mittlere Geschwindigkeit (mean speed): $\langle v \rangle = \sqrt{\cfrac{8k_B T}{\pi m}}$
• Quadratisches Mittel der Geschwindigkeit (RMS speed): $v_{rms} = \sqrt{\langle v^2 \rangle} = \sqrt{\cfrac{3k_B T}{m}}$

Die durchschnittliche kinetische Energie pro Teilchen bei der Temperatur T beträgt $\cfrac{1}{2}m\langle v^2 \rangle = \cfrac{1}{2}mv_{rms}^2 = \cfrac{3}{2}k_B T$ (basierend auf 3 Freiheitsgraden) und wird nur durch die Temperatur bestimmt. Da in Gasen und Plasmen die durchschnittliche kinetische Energie pro Teilchen eng mit der Temperatur verbunden ist und diese beiden austauschbare physikalische Größen sind, ist es in der Plasmaphysik üblich, die Temperatur in der Energieeinheit eV auszudrücken. Um Verwirrung bei den Dimensionen zu vermeiden, wird die Temperatur als Wert von kT anstelle der durchschnittlichen kinetischen Energie $\langle E_k \rangle$ angegeben.

Die Temperatur T, bei der kT = 1 eV ist, beträgt:

\[\begin{align*} T\mathrm{[K]} &= \frac{1,6 \times 10^{-19}\mathrm{[J]}}{1,38 \times 10^{-23}\mathrm{[J/K]}} \\ &= 11600\mathrm{[K]} \end{align*} \label{eqn:temp_conv_factor}\tag{7}\]

Daher bedeutet in der Plasmaphysik 1 eV = 11600 K, wenn die Temperatur angegeben wird.
z.B. Bei einem Plasma mit einer Temperatur von 2 eV beträgt der kT-Wert 2 eV, und die durchschnittliche kinetische Energie pro Teilchen ist $\cfrac{3}{2}kT=3\mathrm{eV}$.

Außerdem können Plasmen gleichzeitig mehrere Temperaturen haben. In Plasmen ist die Häufigkeit von Kollisionen zwischen Ionen oder zwischen Elektronen größer als die Häufigkeit von Kollisionen zwischen Elektronen und Ionen. Dadurch können Elektronen und Ionen jeweils bei unterschiedlichen Temperaturen (Elektronentemperatur Te und Ionentemperatur Ti) das thermische Gleichgewicht erreichen und separate Maxwell-Boltzmann-Verteilungen bilden. In manchen Fällen können die Elektronentemperatur und die Ionentemperatur stark voneinander abweichen. Wenn ein externes Magnetfeld $\vec{B}$ angelegt wird, können sogar Teilchen derselben Art (z.B. Ionen) je nach ihrer Bewegungsrichtung parallel oder senkrecht zum Magnetfeld unterschiedliche Lorentz-Kräfte erfahren und daher unterschiedliche Temperaturen T⊥ und T∥ haben.

Beziehung zwischen Temperatur, Druck und Dichte

Nach dem idealen Gasgesetz gilt:

\[PV = \left(\frac{N}{N_A}\right)RT = NkT \label{eqn:ideal_gas_law}\tag{8}\]

Daraus folgt:

\[\begin{gather*} P = \frac{NkT}{V} = nkT, \\ n = \frac{P}{kT} \end{gather*} \label{eqn:relation_between_T_P_n}\tag{9}\]

Das heißt, die Dichte des Plasmas ist umgekehrt proportional zur Temperatur (kT) und proportional zum Druck (P).

Klassifizierung von Plasmen: Kaltes Plasma vs. Heißes Plasma

Niedertemperatur- Nichtthermisches kaltes Plasma	Niedertemperatur-Thermisches kaltes Plasma	Hochtemperatur- Heißes Plasma
$T_i \approx T \approx 300 \mathrm{K}$ $T_i \ll T_e \leqslant 10^5 \mathrm{K}$	$T_i \approx T_e \approx T < 2 \times 10^4 \mathrm{K}$	$T_i \approx T_e > 10^6 \mathrm{K}$
Niederdruck ($\sim 100\mathrm{Pa}$) Glimm- und Bogenentladungen	Bogenentladungen bei $100\mathrm{kPa}$ ($1\mathrm{atm}$)	Kinetisches Plasma, Fusionsplasma

Plasmatemperatur

Wenn wir die Elektronentemperatur mit Te, die Ionentemperatur mit Ti und die Temperatur der neutralen Teilchen mit Tg bezeichnen, gilt:

• Kaltes Plasma: Te (>10.000 K) ≫ Ti ≈ Tg (∼100 K) → Nichtgleichgewichtsplasma
• Heißes (thermisches) Plasma: Te ≈ Ti ≈ Tg (>10.000 K) → Gleichgewichtsplasma

Plasmadichte

Wenn wir die Elektronendichte mit ne, die Ionendichte mit ni und die Dichte der neutralen Teilchen mit ng bezeichnen, gilt:

• Kaltes Plasma: ng ≫ ni ≈ ne → Geringer Ionisationsgrad, hauptsächlich neutrale Teilchen
• Heißes (thermisches) Plasma: ng ≈ ni ≈ ne → Hoher Ionisationsgrad

Wärmekapazität des Plasmas (Wie heiß ist es?)

• Kaltes Plasma: Hohe Elektronentemperatur, aber geringe Dichte; hauptsächlich relativ kalte neutrale Teilchen, daher geringe Wärmekapazität und nicht heiß
• Heißes (thermisches) Plasma: Hohe Temperatur von Elektronen, Ionen und neutralen Teilchen, daher hohe Wärmekapazität und heiß