Kontinuierliche und charakteristische Röntgenstrahlung

TL;DR

• Bremsstrahlung: Kontinuierliche Röntgenstrahlung, die entsteht, wenn geladene Teilchen wie Elektronen in der Nähe eines Atomkerns durch elektrische Kräfte beschleunigt werden
• Minimale Wellenlänge: $\lambda_\text{min} = \cfrac{hc}{E_\text{max}} = \cfrac{12400 \text{[Å}\cdot\text{eV]}}{V\text{[eV]}}$
• Charakteristische Röntgenstrahlung: Diskontinuierliche Röntgenstrahlung, die entsteht, wenn ein einfallendes Elektron mit einem Elektron der inneren Atomschale kollidiert und das Atom ionisiert, woraufhin ein Elektron aus einer äußeren Schale den freien Platz einnimmt und dabei Energie in Form von Röntgenstrahlung mit der Energiedifferenz zwischen den beiden Energieniveaus freisetzt

Prerequisites

• Subatomare Teilchen und Atomare Bestandteile

Entdeckung der Röntgenstrahlung

Röntgen entdeckte, dass bei der Bestrahlung eines Targets mit Elektronenstrahlen Röntgenstrahlung entsteht. Da zum Zeitpunkt der Entdeckung nicht bekannt war, dass es sich bei der Röntgenstrahlung um elektromagnetische Wellen handelt, wurde sie als X-Strahlung bezeichnet. Nach ihrem Entdecker wird sie auch Röntgenstrahlung genannt.

Die obige Abbildung zeigt den vereinfachten Aufbau einer typischen Röntgenröhre. In der evakuierten Röhre befinden sich eine Kathode aus Wolframfilament und eine Anode mit dem Target. Wenn zwischen den Elektroden eine Spannung von mehreren zehn kV angelegt wird, werden von der Kathode Elektronen emittiert und auf das Target der Anode beschleunigt, wodurch Röntgenstrahlung entsteht. Die Energieumwandlungseffizienz in Röntgenstrahlung beträgt dabei meist weniger als 1%, während über 99% der Energie in Wärme umgewandelt wird, weshalb zusätzliche Kühlvorrichtungen erforderlich sind.

Bremsstrahlung

Wenn geladene Teilchen wie Elektronen in die Nähe eines Atomkerns kommen, werden sie durch die elektrische Kraft zwischen dem Teilchen und dem Kern stark abgelenkt und abgebremst, wobei Energie in Form von Röntgenstrahlung freigesetzt wird. Da dieser Energieumwandlungsprozess nicht quantisiert ist, weist die emittierte Röntgenstrahlung ein kontinuierliches Spektrum auf. Diese Strahlung wird als Bremsstrahlung bezeichnet.

Die Energie der durch Bremsstrahlung emittierten Röntgenphotonen kann natürlich nicht größer sein als die kinetische Energie der einfallenden Elektronen. Daher gibt es eine minimale Wellenlänge der emittierten Röntgenstrahlung, die sich einfach mit folgender Formel berechnen lässt:

\[\lambda_\text{min} = \frac{hc}{E}. \tag{1}\]

Da das Plancksche Wirkungsquantum $h$ und die Lichtgeschwindigkeit $c$ Konstanten sind, wird diese minimale Wellenlänge nur durch die Energie der einfallenden Elektronen bestimmt. Die Wellenlänge $\lambda$ entsprechend einer Energie von $1\text{eV}$ beträgt etwa $1,24 \mu\text{m}=12400\text{Å}$. Daher gilt für die minimale Wellenlänge $\lambda_\text{min}$ bei einer angelegten Spannung von $V$ Volt:

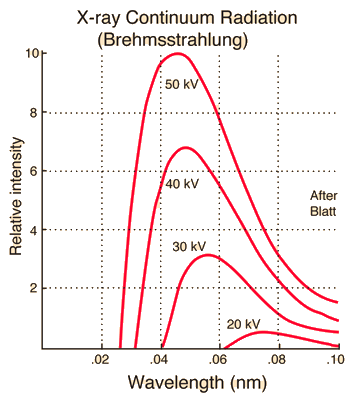
\[\lambda_\text{min} \text{[Å]} = \frac{12400 \text{[Å}\cdot\text{eV]}}{V\text{[eV]}}. \label{eqn:lambda_min}\tag{2}\]

Der folgende Graph zeigt die kontinuierlichen Röntgenspektren bei verschiedenen Spannungen bei konstantem Röhrenstrom. Mit zunehmender Spannung verkürzt sich die minimale Wellenlänge $\lambda_{\text{min}}$, und die Gesamtintensität der Röntgenstrahlung nimmt zu.

Charakteristische Röntgenstrahlung

Wenn die an der Röntgenröhre angelegte Spannung hoch genug ist, können die einfallenden Elektronen mit Elektronen der inneren Atomschalen des Targets kollidieren und das Atom ionisieren. In diesem Fall füllt ein Elektron aus einer äußeren Schale schnell die freie Stelle in der inneren Schale, wobei ein Röntgenphoton mit einer Energie entsprechend der Differenz zwischen den beiden Energieniveaus emittiert wird. Das Spektrum dieser Röntgenstrahlung ist diskontinuierlich und wird durch die charakteristischen Energieniveaus des Targetatoms bestimmt, unabhängig von der Energie oder Intensität des einfallenden Elektronenstrahls. Diese Strahlung wird als charakteristische Röntgenstrahlung bezeichnet.

Siegbahn-Notation

Bildquelle

• Autor: Wikipedia-Benutzer HenrikMidtiby
• Lizenz: CC BY-SA 3.0

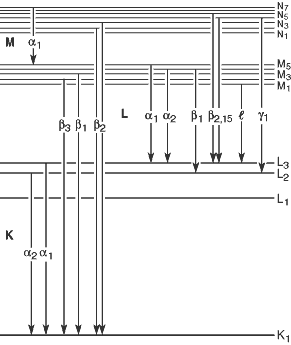
Nach der Siegbahn-Notation wird die Röntgenstrahlung, die entsteht, wenn Elektronen aus der L-Schale, M-Schale, … eine Leerstelle in der K-Schale füllen, wie in der obigen Abbildung als $K_\alpha$, $K_\beta$, … bezeichnet. Mit der Entwicklung des modernen Atommodells nach der Siegbahn-Notation wurde erkannt, dass bei Mehrelektronenatomen die Energieniveaus innerhalb jeder Schale (Energieniveaus mit gleicher Hauptquantenzahl) aufgrund anderer Quantenzahlen unterschiedlich sind. Dies führte zu weiteren Unterteilungen wie $K_{\alpha_1}$, $K_{\alpha_2}$, … für jede $K_\alpha$, $K_\beta$, … Linie.

Diese traditionelle Notation wird in der Spektroskopie noch immer häufig verwendet. Da sie jedoch nicht systematisch ist und oft zu Verwechslungen führt, empfiehlt die International Union of Pure and Applied Chemistry (IUPAC) die Verwendung einer anderen Notation.

IUPAC-Notation

Die von der IUPAC empfohlene Standardnotation für Atomorbitale und charakteristische Röntgenstrahlung ist wie folgt. Zunächst werden den Atomorbitalen Namen nach der folgenden Tabelle zugewiesen:

$n$(Hauptquantenzahl)	$l$(Nebenquantenzahl)	$s$(Spinquantenzahl)	$j$(Gesamtdrehimpulsquantenzahl)	Atomorbital	Röntgennotation
$1$	$0$	$\pm1/2$	$1/2$	$1s_{1/2}$	$K_{(1)}$
$2$	$0$	$\pm1/2$	$1/2$	$2s_{1/2}$	$L_1$
$2$	$1$	$-1/2$	$1/2$	$2p_{1/2}$	$L_2$
$2$	$1$	$+1/2$	$3/2$	$2p_{3/2}$	$L_3$
$3$	$0$	$\pm1/2$	$1/2$	$3s_{1/2}$	$M_1$
$3$	$1$	$-1/2$	$1/2$	$3p_{1/2}$	$M_2$
$3$	$1$	$+1/2$	$3/2$	$3p_{3/2}$	$M_3$
$3$	$2$	$-1/2$	$3/2$	$3d_{3/2}$	$M_4$
$3$	$2$	$+1/2$	$5/2$	$3d_{5/2}$	$M_5$
$4$	$0$	$\pm1/2$	$1/2$	$4s_{1/2}$	$N_1$
$4$	$1$	$-1/2$	$1/2$	$4p_{1/2}$	$N_2$
$4$	$1$	$+1/2$	$3/2$	$4p_{3/2}$	$N_3$
$4$	$2$	$-1/2$	$3/2$	$4d_{3/2}$	$N_4$
$4$	$2$	$+1/2$	$5/2$	$4d_{5/2}$	$N_5$
$4$	$3$	$-1/2$	$5/2$	$4f_{5/2}$	$N_6$
$4$	$3$	$+1/2$	$7/2$	$4f_{7/2}$	$N_7$

Gesamtdrehimpulsquantenzahl $j=|l+s|$.

Die charakteristische Röntgenstrahlung, die bei einem Elektronenübergang von einem höheren zu einem niedrigeren Energieniveau entsteht, wird nach folgender Regel bezeichnet:

\[\text{(Röntgennotation des Endzustands)-(Röntgennotation des Anfangszustands)}\]

Zum Beispiel wird die charakteristische Röntgenstrahlung, die beim Übergang eines Elektrons vom $2p_{1/2}$-Orbital zum $1s_{1/2}$-Orbital entsteht, als $\text{K-L}_2$ bezeichnet.

Röntgenspektrum

Die obige Abbildung zeigt das Röntgenspektrum, das entsteht, wenn ein mit 60kV beschleunigter Elektronenstrahl auf ein Rhodium(Rh)-Target trifft. Man erkennt die glatte, kontinuierliche Kurve der Bremsstrahlung, die gemäß Gleichung ($\ref{eqn:lambda_min}$) nur für Wellenlängen über etwa $0,207\text{Å} = 20,7\text{pm}$ auftritt. Die scharfen Spitzen im Spektrum stammen von der charakteristischen K-Schalen-Röntgenstrahlung des Rhodiumatoms. Da jedes Targetatom ein charakteristisches Röntgenspektrum besitzt, kann man durch die Untersuchung der Wellenlängen der Spitzen im Röntgenspektrum die elementare Zusammensetzung des Targets bestimmen.

Neben $K_\alpha, K_\beta, \dots$ wird auch Röntgenstrahlung niedrigerer Energie wie $L_\alpha, L_\beta, \dots$ emittiert. Diese haben jedoch eine viel geringere Energie und werden meist im Gehäuse der Röntgenröhre absorbiert, bevor sie den Detektor erreichen können.