Analytische Lösung des harmonischen Oszillators (The Harmonic Oscillator)

TL;DR

• Jede Schwingung mit ausreichend kleiner Amplitude kann als einfache harmonische Schwingung (simple harmonic oscillation) angenähert werden, was dem harmonischen Oszillator eine wichtige Bedeutung in der Physik verleiht
• Harmonischer Oszillator: $V(x) = \cfrac{1}{2}kx^2 = \cfrac{1}{2}m\omega^2 x^2$
• Einführung der dimensionslosen Variable $\xi$ und der Energie $K$ in Einheiten von $\cfrac{1}{2}\hbar\omega$:
  • $\xi \equiv \sqrt{\cfrac{m\omega}{\hbar}}x$
  • $K \equiv \cfrac{2E}{\hbar\omega}$
  • $ \cfrac{d^2\psi}{d\xi^2} = \left(\xi^2-K \right)\psi $
• Für $|\xi|^2 \to \infty$ ist die physikalisch zulässige asymptotische Lösung $\psi(\xi) \to Ae^{-\xi^2/2}$, daher

\[\begin{gather*} \psi(\xi) = h(\xi)e^{-\xi^2/2} \quad \text{(wobei }\lim_{\xi\to\infty}h(\xi)=A\text{)}, \\ \frac{d^2h}{d\xi^2}-2\xi\frac{dh}{d\xi}+(K-1)h = 0 \end{gather*}\]

• Wenn wir die Lösung dieser Gleichung als Reihe ausdrücken $ h(\xi) = a_0 + a_1\xi + a_2\xi^2 + \cdots = \sum_{j=0}^{\infty}a_j\xi^j$, erhalten wir

\[a_{j+2} = \frac{(2j+1-K)}{(j+1)(j+2)}a_j\]

• Damit diese Lösung normierbar ist, muss die Reihe $\sum a_j$ endlich sein, d.h. es muss einen ‘größten’ $j$-Wert $n\in \mathbb{N}$ geben, sodass $a_j=0$ für $j>n$, daher
  • $ K = 2n + 1 $
  • $ E_n = \left(n+\cfrac{1}{2} \right)\hbar\omega, \quad n=0,1,2,\dots $
• Im Allgemeinen ist $h_n(\xi)$ ein Polynom $n$-ten Grades in $\xi$, wobei der Rest außer dem vorderen Koeffizienten ($a_0$ oder $a_1$) als Hermite-Polynome (Hermite polynomials) $H_n(\xi)$ bezeichnet wird

\[h_n(\xi) = \begin{cases} a_0 H_n(\xi), & n=2k & (k=0,1,2,\dots) \\ a_1 H_n(\xi), & n=2k+1 & (k=0,1,2,\dots) \end{cases}\]

• Normierte stationäre Zustände des harmonischen Oszillators:

\[\psi_n(x) = \left(\frac{m\omega}{\pi\hbar} \right)^{1/4} \frac{1}{\sqrt{2^n n!}}H_n(\xi)e^{-\xi^2/2}\]

• Eigenschaften des Quantenoszillators
  • Gerade und ungerade Eigenfunktionen wechseln sich ab
  • Auch in Bereichen, die klassisch nicht zugänglich sind (größeres $x$ als die klassische Amplitude für ein gegebenes $E$), ist die Wahrscheinlichkeit, das Teilchen zu finden, nicht Null; es kann mit geringer Wahrscheinlichkeit dort existieren
  • Für alle stationären Zustände mit ungeradem $n$ ist die Wahrscheinlichkeit, das Teilchen im Zentrum zu finden, Null
  • Je größer $n$, desto ähnlicher wird der Quantenoszillator dem klassischen Oszillator

Prerequisites

• Methode der Variablentrennung
• Schrödinger-Gleichung und Wellenfunktion
• Ehrenfest-Theorem
• Zeitunabhängige Schrödinger-Gleichung
• Der eindimensionale unendliche Potentialtopf
• Algebraische Lösung des harmonischen Oszillators

Modellaufbau

Für die Beschreibung des harmonischen Oszillators in der klassischen Mechanik und die Bedeutung des harmonischen Oszillator-Problems siehe den vorherigen Beitrag.

Der harmonische Oszillator in der Quantenmechanik

Das quantenmechanische Problem des harmonischen Oszillators besteht darin, die Schrödinger-Gleichung für das Potential

\[V(x) = \frac{1}{2}m\omega^2 x^2 \label{eqn: potential_omega}\tag{1}\]

zu lösen. Die zeitunabhängige Schrödinger-Gleichung für den harmonischen Oszillator lautet

\[-\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2} + \frac{1}{2}m\omega^2x^2\psi = E\psi \label{eqn:t_independent_schrodinger_eqn}\tag{2}\]

Es gibt zwei völlig unterschiedliche Ansätze zur Lösung dieses Problems. Der eine ist die analytische Methode unter Verwendung von Potenzreihen (power series), der andere ist die algebraische Methode unter Verwendung von Leiteroperatoren (ladder operators). Die algebraische Methode ist schneller und einfacher, aber es ist auch notwendig, die analytische Lösung mit Potenzreihen zu studieren. Wir haben zuvor die algebraische Lösungsmethode behandelt, hier behandeln wir die analytische Lösungsmethode.

Umformung der Schrödinger-Gleichung

Durch Einführung der dimensionslosen Variable

\[\xi \equiv \sqrt{\frac{m\omega}{\hbar}}x \label{eqn:xi}\tag{3}\]

können wir die zeitunabhängige Schrödinger-Gleichung ($\ref{eqn:t_independent_schrodinger_eqn}$) vereinfacht wie folgt schreiben:

\[\frac{d^2\psi}{d\xi^2} = \left(\xi^2-K \right)\psi. \label{eqn:schrodinger_eqn_with_xi}\tag{4}\]

Hier ist $K$ die Energie in Einheiten von $\cfrac{1}{2}\hbar\omega$.

\[K \equiv \frac{2E}{\hbar\omega}. \label{eqn:K}\tag{5}\]

Nun müssen wir die so umgeschriebene Gleichung ($\ref{eqn:schrodinger_eqn_with_xi}$) lösen. Für sehr große $\xi$ (d.h. für sehr große $x$) gilt $\xi^2 \gg K$, sodass

\[\frac{d^2\psi}{d\xi^2} \approx \xi^2\psi \label{eqn:schrodinger_eqn_approx}\tag{6}\]

wird, und eine approximative Lösung dafür ist

\[\psi(\xi) \approx Ae^{-\xi^2/2} + Be^{\xi^2/2} \label{eqn:psi_approx}\tag{7}\]

Der $B$-Term divergiert jedoch für $|x|\to \infty$ und kann nicht normiert werden, sodass die physikalisch zulässige asymptotische Lösung

\[\psi(\xi) \to Ae^{-\xi^2/2} \label{eqn:psi_asymp}\tag{8}\]

ist. Trennen wir nun den Exponentialteil ab und schreiben

\[\psi(\xi) = h(\xi)e^{-\xi^2/2} \quad \text{(wobei }\lim_{\xi\to\infty}h(\xi)=A\text{)} \label{eqn:psi_and_h}\tag{9}\]

Um den Exponentialterm $e^{-\xi^2/2}$ zu ermitteln, haben wir im Ableitungsprozess eine Näherungsmethode verwendet, um die Form der asymptotischen Lösung zu finden, aber die daraus resultierende Gleichung ($\ref{eqn:psi_and_h}$) ist keine Näherung, sondern eine exakte Gleichung. Diese Trennung der asymptotischen Form ist der Standardschritt beim Lösen von Differentialgleichungen in Form von Potenzreihen.

Wenn wir Gleichung ($\ref{eqn:psi_and_h}$) differenzieren, um $\cfrac{d\psi}{d\xi}$ und $\cfrac{d^2\psi}{d\xi^2}$ zu erhalten, erhalten wir

\[\begin{gather*} \frac{d\psi}{d\xi} = \left(\frac{dh}{d\xi}-\xi h \right)e^{-\xi^2/2}, \\ \frac{d^2\psi}{d\xi^2} = \left(\frac{d^2h}{d\xi^2}-2\xi\frac{dh}{d\xi}+(\xi^2-1)h \right)e^{-\xi^2/2} \end{gather*}\]

sodass die Schrödinger-Gleichung ($\ref{eqn:schrodinger_eqn_with_xi}$) nun zu

\[\frac{d^2h}{d\xi^2}-2\xi\frac{dh}{d\xi}+(K-1)h = 0 \label{eqn:schrodinger_eqn_with_h}\tag{10}\]

wird.

Potenzreihenentwicklung

Nach dem Taylorschen Satz (Taylor’s theorem) kann jede glatte Funktion als Potenzreihe dargestellt werden. Versuchen wir also, die Lösung von Gleichung ($\ref{eqn:schrodinger_eqn_with_h}$) in Form einer Reihe in $\xi$ zu finden:

\[h(\xi) = a_0 + a_1\xi + a_2\xi^2 + \cdots = \sum_{j=0}^{\infty}a_j\xi^j \label{eqn:h_series_exp}\tag{11}\]

Durch Differenzieren jedes Terms dieser Reihe erhalten wir die folgenden zwei Gleichungen:

\[\begin{gather*} \frac{dh}{d\xi} = a_1 + 2a_2\xi + 3a_3\xi^2 + \cdots = \sum_{j=0}^{\infty}ja_j\xi^{j-1}, \\ \frac{d^2 h}{d\xi^2} = 2a_2 + 2\cdot3a_3\xi + 3\cdot4a_4\xi^2 + \cdots = \sum_{j=0}^{\infty} (j+1)(j+2)a_{j+2}\xi^j. \end{gather*}\]

Wenn wir diese beiden Gleichungen wieder in die Schrödinger-Gleichung (Gleichung [$\ref{eqn:schrodinger_eqn_with_h}$]) einsetzen, erhalten wir:

\[\sum_{j=0}^{\infty}[(j+1)(j+2)a_{j+2} - 2ja_j + (K-1)a_j]\xi^j = 0. \label{eqn:schrodinger_eqn_power_series}\tag{12}\]

Aufgrund der Eindeutigkeit der Potenzreihenentwicklung muss der Koeffizient für jede Potenz von $\xi$ gleich Null sein, sodass

\[(j+1)(j+2)a_{j+2} - 2ja_j + (K-1)a_j = 0\] \[\therefore a_{j+2} = \frac{(2j+1-K)}{(j+1)(j+2)}a_j. \label{eqn:recursion_formula}\tag{13}\]

Diese Rekursionsformel (recursion formula) ist äquivalent zur Schrödinger-Gleichung. Wenn zwei beliebige Konstanten $a_0$ und $a_1$ gegeben sind, können alle Koeffizienten der Lösung $h(\xi)$ bestimmt werden.

Allerdings kann die so erhaltene Lösung nicht immer normiert werden. Wenn die Reihe $\sum a_j$ eine unendliche Reihe ist (wenn $\lim_{j\to\infty} a_j\neq0$), wird die obige Rekursionsformel für sehr große $j$ näherungsweise zu

\[a_{j+2} \approx \frac{2}{j}a_j\]

und eine approximative Lösung dafür ist

\[a_j \approx \frac{C}{(j/2)!} \quad \text{(}C\text{ ist eine beliebige Konstante)}\]

In diesem Fall wird für große $\xi$-Werte, bei denen die höheren Terme dominant werden,

\[h(\xi) \approx C\sum\frac{1}{(j/2)!}\xi^j \approx C\sum\frac{1}{j!}\xi^{2j} \approx Ce^{\xi^2}\]

und wenn $h(\xi)$ diese Form $Ce^{\xi^2}$ annimmt, wird $\psi(\xi)$ in Gleichung ($\ref{eqn:psi_and_h}$) zu $Ce^{\xi^2/2}$, was für $\xi \to \infty$ divergiert. Dies entspricht der nicht normierbaren Lösung mit $A=0, B\neq0$ in Gleichung ($\ref{eqn:psi_approx}$).

Daher muss die Reihe $\sum a_j$ endlich sein. Es muss einen ‘größten’ $j$-Wert $n\in \mathbb{N}$ geben, sodass $a_j=0$ für $j>n$, und damit dies der Fall ist, muss für ein nicht-nulles $a_n$ gelten $a_{n+2}=0$, was aus Gleichung ($\ref{eqn:recursion_formula}$) bedeutet, dass

\[K = 2n + 1\]

sein muss. Wenn wir dies in Gleichung ($\ref{eqn:K}$) einsetzen, erhalten wir die physikalisch erlaubten Energien

\[E_n = \left(n+\frac{1}{2} \right)\hbar\omega, \quad n=0,1,2,\dots \label{eqn:E_n}\tag{14}\]

Damit haben wir die Energiequantisierungsbedingung aus Gleichung (21) der algebraischen Lösung des harmonischen Oszillators auf eine völlig andere Weise erhalten.

Hermite-Polynome (Hermite polynomials) $H_n(\xi)$ und stationäre Zustände $\psi_n(x)$

Hermite-Polynome $H_n$

Im Allgemeinen ist $h_n(\xi)$ ein Polynom $n$-ten Grades in $\xi$, und für gerade $n$ enthält es nur gerade Potenzen, für ungerade $n$ nur ungerade Potenzen. Der Rest außer dem vorderen Koeffizienten ($a_0$ oder $a_1$) wird als Hermite-Polynom (Hermite polynomial) $H_n(\xi)$ bezeichnet.

\[h_n(\xi) = \begin{cases} a_0 H_n(\xi), & n=2k & (k=0,1,2,\dots) \\ a_1 H_n(\xi), & n=2k+1 & (k=0,1,2,\dots) \end{cases}\]

Traditionell werden die Koeffizienten so gewählt, dass der Koeffizient des höchsten Terms von $H_n$ $2^n$ ist.

Hier sind die ersten paar Hermite-Polynome:

\[\begin{align*} H_0 &= 1 \\ H_1 &= 2\xi \\ H_2 &= 4\xi^2 - 2 \\ H_3 &= 8\xi^3 - 12\xi \\ H_4 &= 16\xi^4 - 48\xi^2 + 12 \\ H_5 &= 32\xi^5 - 160\xi^3 + 120\xi \\ &\qquad\vdots \end{align*}\]

Stationäre Zustände $\psi_n(x)$

Die normierten stationären Zustände für den harmonischen Oszillator lauten:

\[\psi_n(x) = \left(\frac{m\omega}{\pi\hbar} \right)^{1/4} \frac{1}{\sqrt{2^n n!}}H_n(\xi)e^{-\xi^2/2}.\]

Dies stimmt mit dem Ergebnis überein, das wir in der algebraischen Lösung des harmonischen Oszillators (Gleichung [27]) erhalten haben.

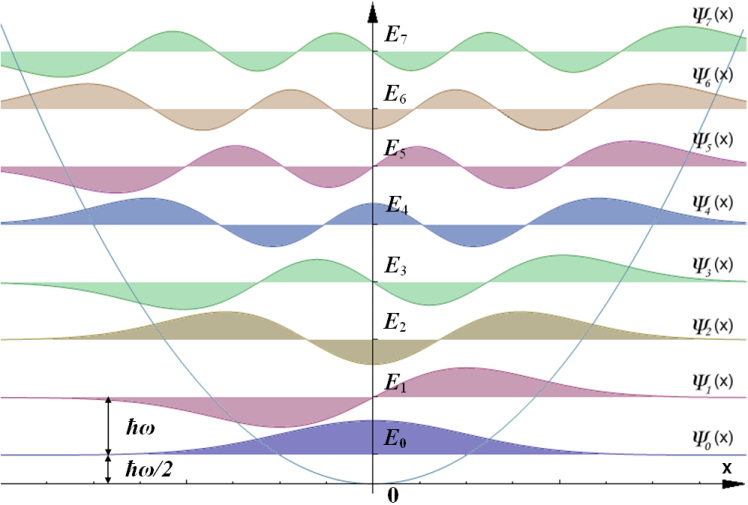
Das folgende Bild zeigt die stationären Zustände $\psi_n(x)$ und die Wahrscheinlichkeitsdichten $|\psi_n(x)|^2$ für die ersten 8 $n$-Werte. Man kann sehen, dass sich gerade und ungerade Eigenfunktionen des Quantenoszillators abwechseln.

Bildquelle

• Autor: Wikimedia-Benutzer AllenMcC
• Lizenz: CC BY-SA 3.0

Bildquelle

• Autor: Wikimedia-Benutzer AllenMcC
• Lizenz: Public Domain

Der Quantenoszillator unterscheidet sich erheblich vom entsprechenden klassischen Oszillator, nicht nur in der Quantisierung der Energie, sondern auch in der Wahrscheinlichkeitsverteilung der Position $x$, die einige merkwürdige Eigenschaften aufweist.

• Auch in Bereichen, die klassisch nicht zugänglich sind (größeres $x$ als die klassische Amplitude für ein gegebenes $E$), ist die Wahrscheinlichkeit, das Teilchen zu finden, nicht Null; es kann mit geringer Wahrscheinlichkeit dort existieren
• Für alle stationären Zustände mit ungeradem $n$ ist die Wahrscheinlichkeit, das Teilchen im Zentrum zu finden, Null

Je größer $n$ wird, desto ähnlicher wird der Quantenoszillator dem klassischen Oszillator. Das folgende Bild zeigt die klassische Wahrscheinlichkeitsverteilung der Position $x$ (gestrichelte Linie) und den Quantenzustand $|\psi_{30}|^2$ (durchgezogene Linie) für $n=30$. Wenn man die unebenen Teile glättet, stimmen die beiden Graphen ungefähr überein.

Bildquelle

• Autor: Wikimedia-Benutzer AkanoToE
• Lizenz: Public Domain

Interaktive Visualisierung der Wahrscheinlichkeitsverteilungen des Quantenoszillators

Das Folgende ist eine reaktive Visualisierung basierend auf Plotly.js, die ich selbst erstellt habe. Sie können den $n$-Wert mit dem Schieberegler anpassen und die klassische Wahrscheinlichkeitsverteilung sowie die Form von $|\psi_n|^2$ für die Position $x$ überprüfen.

• Originalvisualisierung: https://www.yunseo.kim/physics-visualization/quantum-harmonic-oscillator
• Quellcode: yunseo-kim/physics-visualization Repository
• Lizenz: Siehe hier

Wenn Sie Python auf Ihrem eigenen Computer verwenden können und eine Umgebung mit den Bibliotheken Numpy, Plotly und Dash installiert haben, können Sie auch das Python-Skript /src/quantum_oscillator.py im selben Repository ausführen, um die Ergebnisse zu sehen.